VII. Disposal of high level wastes
(Leader Dr. A.R.Kotelnikov)Kotova N.P., Ivanov I.P. Thermodynamic modelling of leaching of Na-Al-phosphate glass containing radioactive 90Sr and 137Cs isotopes by underground water under burial conditions.
We have carried out a numerical modelling of local equilibrium leaching of technologic glass on the base of the system (Na,Cs)2O-SrO-Al2O3-P2O5-H2O, open for Na2O and P2O5 components in the range of T=25-350oC at Psat. The calculations were performed using Yu.V.Shvarov's program.
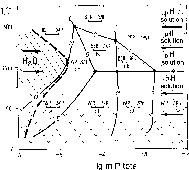
The glass is unstable under the condition of a water excess above 90oC. It crystallizes with the formation of readily soluble sodium phosphates and low-soluble strontium and aluminium phosphates and hydrated alumina compounds. At the first stage strontium phosphates and isomorphous Cs escape from the system with the filtering underground waters. At the second stage phosphorus is leached in a step-wise manner, as is shown in fig.1. A dynamic equilibrium is reached at pHH2O=pHsol in the system. This equilibrium is shown in fig.1 in a discontinuous curve. Stable low-soluble associations DSP+GO and DSP+SAP remain in the burial site. The concentration of strontium, in the solution does not exceed n.10-7-n.10-6 mole/kg H2O.
Fixation of Cs necessitates special barrier constructions whereas no such constructions are needed for Sr.
Fig.1. T-lgmPtot diagram of the system SrO-Al2O3-P2O5-H2O at saturated water vapour.
SPH-strontium hydrophosphate SrHPO4, SAP-strontium hydroxide apatite Sr10(PO4)6.(OH)2, GO-goyazite - SrAl3(PO4)2(OH)5.H2O, BER-berlinite-AlPO4, VAR - variszite-AlPO4.2H2O, DSP-diaspore - AlOOH. 1-11-monovariant lines, ticks- region of delayed reactions, arrows pHsol - direction of increase of the system's solution pH, arrows H2O - direction of water, motion, region to the right of the discontinuous line - region of phosphorus leaching, region shaded with skew lines - region where no phosphorus leaching occurs.
Kotelnikov A.R., Koval'skii A.M., Akhmedzhanova G.M., Chichagov A.V., and Orlova A.I. 2Synthesis and X-ray study of (Na,K)-zirconium phosphates
Department of Chemistry, Nizhnii Novgorod State University
The phases with variable composition based on complex zirconium and alkali elements orthophosphates (NZP) phases were studied in [1, 2]. Due to the structure capable to embed various elements and stable under hydrothermal conditions and in radiation fields, these phases can be promising matrix materials for the development of methods for solidification of radioactive waste, including those with a high alkali-salt content.
The purpose of this work is to synthesize the phases, to study cation-exchange reactions in the (Na,K)Zr2(PO4)3-solution (NaCl+KCl+H2O) system, and to refine unit cell parameters of solid solutions of Na1-xKxZr2(PO4)3 formed on the basis of isovalence isomorphism of sodium and potassium in this system.
The cation-exchange reaction
NaZr2(PO4)3 + KCl ↔ KZr2(PO4)3 + NaCl, (1)
was studied at temperatures of 450-650oC and pressures of 1-2 kbar.
78
The experiments were carried out by the apparatus procedure in high-pressure setups with a cool seal and external heating. The duration of experiments was 21 to 39 days, and the approach to the equilibrium isotherm was performed from two sides. The phase and chemical composition of solid products of experiments was determined by X-ray and microprobe methods, and solutions were analyzed by the AAS method.
The results of experiments showed that the distribution of Na and K between zirconium phosphates and fluid is nonideal, and potassium enriches zirconium phosphate relative to the fluid over the whole composition interval. The distribution coefficients of potassium and sodium in the zirconium phosphate-solution system were calculated by the equation:
KD = NZPx (1-flx)/[(1-NZPx) flx], (2)
where x is the molar fraction of potassium in zirconium phosphate.
The experimental data describing the dependence of lnKD on the composition (x) at different temperatures are approximated by equations (3)-(5):
4500Ñ: lnKD = -0.03165 + 4.0567× (x) - 0.307579× (x2)(n = 7, Ex = 0.13), (3)
5500Ñ: ln KD = -1.2582 + 7.28314× (x) - 3.62246× (x2)(n =10, Ex = 0.13), (4)
6500Ñ: ln KD = -1.14827 + 6.113392× (x) - 3.45608× (x2)(n =11, Ex = 0.08), (5)
where n is the number of experimental points, and Ex is the calculation error.
According to the X-ray data, the phases under study form a series of structural analogs that are characterized by space group R3c. The crystallographic parameters of the NZP phases change smoothly as the composition changes. Therefore, the formation of solid solutions of replacement Na1-xKxZr2(PO4)3 occurred in the system.
The concentration dependences of the cell parameters of solid solutions of the NZP structure a = f(x), c = (f(x), and V = (f(x) are characterized by nonlinear curves and can be described by the third-order polynomials:
a= 8.804456 - 0.049698.x - 0.0749567.x2 + +0.033362.x3 [A] (± 0.002), (6)
c= 22.758907 + 0.903066.x + 1.365036.x2 -- 1.100030.x3 [A] (± 0.001), (7)
V=1527.871 + 44.909617.x + 58.897387.x2 -- 58.759463.x3 [A]3 (± 0.2), (8)
where x is the molar fraction of potassium in the solid solution of NZP.
The following equation was derived from (6)-(8) for the estimations of compositions of solid solutions Na1-xKxZr2(PO4)3 by the known parameters a, c, and V:
x = A + B(p-M) + C(p-M)2 + D(p-M)3, where p are the cell parameters, and A, B, C, and D are the coefficients presented in table.
P |
M |
A |
B |
C |
D |
Ex |
| a, A | 8.7 | 1.085844 | -7.327931 | -25.108137 | -14.631875 | 0.02 |
| c, A | 22.7 | -0.0742971 | 1.238594 | -1.052112 | 0.604380 | 0.01 |
| V, A3 | 1527.5 | -0.0244179 | 0.0272337 | -0.0007265 | 0.000012526 | 0.02 |
The dependences obtained make it possible to estimate the composition of solid solutions with an average accuracy of +2 mol.%.
The calculated Margules parameters for the description of the excessive volume of mixing sodium-potassium zirconium phosphates are the following: W1 = 12.39(55); W2 = 0.042(10) cm3/mol.
References:
Petukhov P.A. New form of thermodynamic models of surplus solid solution intermixing properties.
solid solution intermixing properties.
In order to correlate phase equilibria data with thermochemical and crystallochemical solid solution data one has to use such models of surplus intermixing properties which are thermodynamically correct in a broad range of parameters, including temperatures close to 0 K. A significant condition for thermodynamic correctness of the model is the correlation of temperature dependences of the surplus intermixing functions: enthalpy (He), entropy (Se), Gibbs energy (Ge), and isobaric thermal capacity (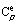 ). This condition will be fulfilled in the case that the temperature dependence of the surplus isobaric thermal capacity be represented as the parametric function, and the temperature dependence of the other surplus intermixing characteristics be given though this function. The following demands are made on the temperature dependence of the surplus isobaric thermal capacity:
). This condition will be fulfilled in the case that the temperature dependence of the surplus isobaric thermal capacity be represented as the parametric function, and the temperature dependence of the other surplus intermixing characteristics be given though this function. The following demands are made on the temperature dependence of the surplus isobaric thermal capacity:
1) the value of the surplus isobaric thermal capacity tends to zero as T=0 K is approached;
79
2) the temperature dependence of the surplus thermal capacity can have a maximum and allow for the inversion;
3) the value of the surplus intermixing entropy, derived from this dependence, is defined and limited for every temperature value.
This approach was successfully tested at data correlation for a ternary feldspar solution. The simple fraction -rational function was used as the parametric expression for the temperature dependence of the surplus isobaric thermal capacity
Cpe(T) = A(X) T / (a2+T2), (1)
where A(X), a are parameters. The dependence of the A(X) parameter on the solution composition is analogous to that considered in the work [1]. The a parameter defines the temperature at which the surplus intermixing thermal capacity reaches a maximum, and the relationship between these parameters defines the value of the surplus intermixing thermal capacity.
The corresponding expressions for surplus intermixing enthalpy and entropy had the form :
He (T) = ò 0T Cpe (T) dT = A(X) ln(1+T2/a2) / 2, (2)
Se (T) = ò 0T Cpe (T)/T dT = A(X) arctan(T/a) / a, (3)
The solution is fully misordered at sufficiently high temperature, and the solution intermixing entropy is near ideal. As the temperature is decreased, the surplus entropy starts manifesting itself. At T=0 K the surplus solution entropy reaches the value of the integral (3) taken with unlike sign within integration from zero to infinity. In this way one can substantiate the So parameters, gives surplus intermixing entropy at T=0 K, which is being calculated by the expression (3):
S0 = -lim { A(X) arctan(T/a) / a } = -1.571 A(X)/a T® ¥, (4).
The ideal integral intermixing entropy (Sid) was defined as
Sid(X) = -R å k xk ln(xk), (5)
where K is the index corresponding to the solution components, R is the universal gas constant; xk is the molar fraction of the k-th component in solution.
The volume intermixing effects were taken into account like in the work [1]. The final expression for the integral intermixing free energy (Gm) had the form:
Gm(P,T,X) = PVe + He T (Se+ S0+ Sid) = = PVe(X) +A(X) ln(1+T2/a2)/2 T{A(X) ..arctan(T/a)/a 1.571A(X)/a +Sid(X)}, (6)
Reference:
Suvorova V.A., Kotelnikov A.R. Synthesis of matrix materials on the base of phosphate solid solutions for immobilization of rare-earth elements and HLW actinides.
The mass disposal of high level waste necessitates the material of which the production procedure would not be expensive and energy-consuming. Ceramics produced by sintering mineral grains of finely ground rocks and calcinated radioactive waste can be used as such material. The validity of rocks for binding Na, Ca, Cs, and Sr from high-level waste was shown in [1]. Based on the requirement of easy incorporation of lanthanoids and REE into the mineral structure we took for our runs rocks bearing REE alkali pyroxenes and silicates, i.e. granites and tuffs.
Monazite was used as the mineral - concentrator of REE (La, Ce). The synthesized monazite specimens (REE orthophosphates) were mixed with rocks from the Mayak proving grounds (tuffs and granites) in the ratio (75-65)/(25-35), the mixture was ground to homogeneous composition, compacted to tables at room temperature, and annealed at 1080oC for 3 days in the first run series. The leaching rate had a maximum value for all the samples in the first 8 days of the runs 0.002-0.015% of the REE contained in the sample transferred into the leaching medium, over that period. The ceramics quality was estimated from leaching rates of the elements from the samples in distilled water at 90oC, according to the MCC-1 IAEA test [2]. The run results are listed in the table and illustrated in figures 1 and 2 [3].
Fig.1. Kinetics of La and Ce leaching from ceramic samples
Fig.2. Kinetics of phosphorus leaching from ceramic samples
80
Table. Leaching rate V (g/m2.days) of the elements from ceramic samples
N and composit. of the sample |
Density, g/cm3 | Leach. elem. | Wt% in start sample | 0-1 day | 1-7 day | 7-14 day | 14-28 day |
Fm1 LaPO4 + Granite Le2 |
1.91 |
Al P La Na |
5.56 2.94 4.65 3.32 |
0.890 3.300 0.079 7.802 |
0.125 1.260 0.025 2.030 |
0.050 0.400 0.078 0.580 |
0.022 0.230 0.008 0.386 |
Fm2 LaPO4 + Granite Le7 |
1.95 |
Al P La Na |
5.41 4.39 8.54 4.02 |
1.020 1.540 0.079 - |
0.240 0.650 0.008 0.991 |
0.056 0.180 0.009 0.352 |
0.020 1.103 0.009 0.191 |
Fm3 CePO4 + Granite Le2 |
1.90 |
Al P Ce Na |
3.23 10.24 30.66 0.82 |
0.280 0.010 0.029 - |
0.170 - 0.005 0.140 |
- 0.012 0.005 0.050 |
0.001 0.048 0.003 0.022 |
Fm 4 CePO4 + Granite Le7 |
2.24 |
Al P Ce Na |
3.16 12.16 33.29 0.64 |
0.304 0.009 0.183 - |
0.110 0.148 0.004 - |
0.004 - 0.002 - |
0.002 0.006 0.002 - |
Fm5 CePO4 + tuff |
2.05 |
Al P Ce Na |
6.55 8.31 24.58 1.00 |
0.220 0.220 0.013 - |
0.103 0.075 0.004 0.186 |
0.005 0.006 0.003 0.067 |
0.004 - 0.003 0.029 |
In order to upgrade the ceramics quality, we have studied the processes of phase transitions in rocks and shown that sintering occurs at 1040oC. This temperature was taken to be optimal. At lower annealing temperature the ceramics produced is loose and leaching-unstable, at higher temperature it transforms to thermally and chemically unstable glass. In the course of the process a quartz-feldsparic melt appears between charge grains (silicate and orthophosphate grains) at the boundaries of which REE diffusion and intergranular melt cementation proceeds.
As a result of sintering at 1040oC ceramic materials were obtained having the density 2.74-2.89 g/cm3 and REE concentration to 20 wt% and exhibiting a high leaching stability: the leaching rate of Ce was 0.000025 g/(m2.d) after 30-day duration (only 5.10-5% Ce contained in the sample transfers to the leaching medium over a 8-day period). These rates are of the same order of magnitude as the Synrock samples [4]. The obtained predominance of leaching rate of phosphorus over that of REE suggests that the REE are bound in the structures of freshly formed minerals, in the case of granite Ce is bound to orthite (allanite).
So, we synthesized a stable ceramic material for immobilization of long-lived radionuclides, which satisfies the principle of phase and chemical compatibility [5] in the matrix-host rock system, making it possible to minimize the processes of radionuclide leaching to the environment. Moreover, the phase-radionuclide concentrator in the proposed matrix- is surrounded with a synthetic rock layer that, in itself, is an additional protective barrier.
The RF patent N2128377 for this method "REE ceramitization technique" is received 27 March, 1999.
References:
81