V. Experimental and theoretical studies of fluid systems (Leader Dr. M.A.Korzhinskiy, Dr. L.Z.Lakshtanov)
Zakirov I.V. and Sretenskaya N.G. Experimental determination of the gas clasterization degree at near-critical conditions: case of CO2
At present, there are numerous studies proposing various equations of state for simple and complex gas systems. These studies are based on the modern progress in molecular dynamics, quantum physics, and computer simulation. Recently, we proposed a physico chemical model of real gas state dealing with the real gas as a mixture of monomers, dimers, trimers etc. (clasters) [1,2]. In the framework of this model we have worked out and realized the experimental method allowing to quantitatively estimate a degree of real gas nonideality.
The installation and method are developed for experimental study of two gas mixing as a function of initial pressure, temperature, and mole fractions of the components. The installation is a unique fully automatic device allowing to continuously record the pressure changes at constant temperature during 2 hours. In that operation, temperature is maintained with the accuracy 0.1oC, while pressure is measured each 20 ms, averaging 10 points with precision 0.01 atm [3]. The experimental data on Ar and CO2 mixing have obtained on the isotherms 25 and 33oC (critical temperature of CO2 = 31.40oC) at initial pressures 30, 40, 50, 60, and 70 atm (critical pressure of CO2 = 73.83 bars), and Ar mole fractions 0.02, 0.05, 0.14, 0.25, and 0.5. It is shown that pressure increases at constant temperature in all cases. The effect of pressure increase at constant temperature 25oC increases from 1.2% at pressure 30 atm to 9% at 60 atm, while at temperature 33oC it changes from 1% at 40 atm to 20% at 70 atm (Fig.1). Argon is an ideal gas under above conditions and its density is essentially constant. Therefore, the pressure increase may be explained by a reduction in degree of clasterization of the dense (nonideal) CO2. Argon, with a higher kinetic energy at given conditions, breaks down the carbon dioxide clasters and hence, increases a number of free particles. The more particles are in the reaction vessel the more impacts occur with its walls. This leads to an increase in total pressure. The investigation of excess pressure dependence on the argon mole fractions allowed to determine a value of pressure increase at disintegration of one CO2 claster, assuming that dimers prevail under given conditions. These results permitted to calculate the degree of CO2 clasterization at various temperatures and pressures. The number of CO2 dimers at temperature 25oC is 20% at pressure 30 atm and 88% at pressure 60 atm, while at temperature 33oC it is 20% at 40 atm and 48% at 60 atm. The obtained data explain the behavior of CO2 fugacity coefficients and CO2 activity in natural hydrothermal fluid.
69
Fig.1. The effect of pressure increase versus temperature and initial pressure.
References:
#Gorbaty Yu.E. A model for transition of liquid water into the supercritical state
The practically consequential problem of transition of liquids into the supercritical state have been already discussed (1,2). An assumption was made that a substance loses properties of a liquid as temperature of the substance reaches the critical value. On the other hand, the question: whether a supercritical phase is a liquid or a gas seems to have no physical meaning. It is well known that there is no qualitative difference between a liquid and its vapour. This means that we can distinguish between a liquid and gas if only both these states coexist, that is, bellow the critical temperature. Still, to predict properties of a supercritical fluid as a solvent or a chemical agent it is helpful to envisage the physical state of the supercritical fluid under a variety of external conditions.
It is well-known that the reason for the very high critical temperature of H2O is hydrogen bonding between water molecules. The hydrogen bonds are subject to structure fluctuations, that is, they rearrange incessantly. Nevertheless, at ambient conditions they at every moment form a boundless three-dimensional network. The connectivity of the network can be characterised by the probability of hydrogen bonding Pb that is evidently equal to 1 for ice I and to 0 for the water vapour at zero density. As temperature increases, the amount of intact bonds decreases, leaving more and more gaps in the network. Evidently, it must inevitably lead to such a situation when the infinite cluster of water molecules cannot exist anymore. In terms of the percolation theory this means that the connectivity of network has reached the percolation threshold Pc.
The temperature dependence of Pb has become known from experimental data and results of computer simulations. Some experimental and theoretical data on the probability of hydrogen bonding Pb in a rather wide range of densities are presented in Fig. 1.
The scatter of the experimental data in Fig.1 can be approximated with the linear equation
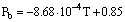, [1]
which describes the temperature behaviour of Pb in the range of densities 0.7-1.1 g cm-3 with the accuracy ±0.1. However, this is a very rough estimate inasmuch as it embraces the data obtained with quite different methods in a wide range of densities and pressures. One can also notice that tolerances of validity of Eqn [1] are set too high. In fact, the uncertainty of Pb at approaching the critical temperature is about ±0.05. At critical temperature the value of Pb is in the limits from 0.28 to 0.36.
Fig. 1. The temperature dependence of Pb in water. Circles, IR data on 
OH; squares, IR data on OD; triangles, x-ray scattering data; dashed line, MC simulations.
The upper estimate is rather close to the percolation threshold suggested by Stanley and Teixeira who had chosen Pc=0.39, assuming that the random network of hydrogen bonds in water resembles topologically the diamond-like one. However, the question of the realistic value of Pc for the water fluid is still open. It can hardly be possible at present to identify the incessantly changed infinite cluster of hydrogen-bonded molecules and to calculate the exact value of Pc. It seems, however, that a bond percolation model is more relevant to the water structure. The bond percolation threshold for a given system is known to be lower than for the site percolation in the same system. Perhaps, the most appropriate model for water would be the "Swiss cheese" model (continuum percolation) for which Pc is also less than 0.39.
#The support from INTAS (Grant 96-1989) and the RFBR (Grants N 97-05-65956 and 99-05-65554) is greatly appreciated.
70
One can see that the situation with the realistic value of Pc for the water structure is rather complicated. Yet, taking into account numerous data on Pc for different structures, it would not seem incredible to estimate the uncertainty as 0.3<Pc<0.4 (hatched area in the Fig. 1)_. Then, as may be seen in Fig. 1, Pb in a wide range of densities approaches Pc at the critical or slightly lower temperature. This means that above the critical isotherm the infinite cluster of hydrogen bonded molecules does not exist.
Thus, at least in the case of water, the infinite cluster is a characteristic feature of the liquid state that lasts up to the critical temperature. The abnormally high critical temperature of water can be explained just in this way. Incidentally, as pressure and density increase, the finite hydrogen bonded clusters of molecule in the coexisting gas phase grow in size and tend to merge into the infinite cluster, so that at approaching the critical point the bond connectivity in gas and liquid tends to be equal.
We thereby arrive at the conclusion that a qualitative difference between liquid water and water vapour does exist. There is a property (infinite cluster) which is intrinsic for liquid water and is not present in gas. Using the terms of percolation theory, we may also say that the character of fractal symmetry in a liquid and its gas is quite different. Although such a property is inferior to the perfect symmetry observed in crystalline solids, it disappears by jump at the transition of liquid water into gas under subcritical conditions. If it is so, the connectivity of hydrogen bonded structure of water may be a suitable and unconditional criterion for the analysis of the physical state of supercritical water.
One should not expect very sharp changes in the properties of a substance as it gets over the percolation threshold. It is clear that the transition into the supercritical state can take place not exactly at the critical temperature but in some temperature range, in which the fluctuations of the nearest environment and thereby of the network connectivity cause alternate appearance and disappearance of the infinite cluster till it cannot arise anymore. Analysis of the thermodynamic data shows that this "illegal" transition reveals itself in the first derivatives and the high order derivatives of thermodynamic quantities. It can also be seen that transition of liquid water in the supercritical state takes place in a rather narrow temperature range near the critical point but this interval broadens at moving away from it. One can also notice that the transition zone broadens toward slightly higher temperatures with the pressure increase.
References:
Korzhinsky M.A., Zhdanov N.N., Tkachenko S.I., and Bocharnikov R.E. New equipment for the measurements of high temperature volcanic gas conditions
One of the main problems in modern volcanic gas geochemistry is a continuous surveillance of volcanic gas conditions to determine the mechanism of outgassing processes. It is also important in formulation of quantitative criteria for reliable prediction of volcanic eruptions. For this purpose, a new technique (monitoring system) is developed and created. It allows to measure a variety of volcanic gas conditions as well as ambient conditions in automatic operation. The scheme of overall system is shown in Fig.1.
Fig.1 Principal scheme of monitoring system for the measurements of high temperature volcanic gas conditions.
The system includes:
Operation principle and technical characteristics of the sensors.
Temperature gauges.
Pressure transducers.
1. Strain-measuring transducer (D-0.1) is applied for the measurements of atmospheric pressure. The transducer is vacuumed and sealed from one edge that permits to use it as a transducer of absolute pressure. The precision of atmospheric pressure measurements is +4.10-4 atm.
2. The similar pressure transducer (D-0.1) is applied for the excess gas pressure measurements. The gas pressure is transmitted through the quartz tube and connected with the transducer via protecting membrane (Fig.2a). The accuracy of measurements is 1.10-4 atm.
71
3. The main working principle of the sensor for partial hydrogen pressure determination is a selective hydrogen diffusion through the platinum membrane at high temperatures. The sensor is designed as Pt membrane, permeable to hydrogen, and strain-measuring transducer (D-0.1) of absolute pressure, connected with Pt-membrane via metallic capillary (Fig.2b). The distinctive feature of this sensor is high sensitivity up to 1.10-4 atm. It allows to measure the partial hydrogen pressure in gas mixture at atmospheric pressure with precision +1mole%.
Electrochemical sensors.
1. The electrochemical cell, involving internal Pt-electrode, Ni-NiO as a reference buffer, Y-stabilized zirconium oxide ceramics, which conducts O2- ions, and external Pt-electrode, is applied to measure the oxygen activity [1]. The accuracy of oxygen fugacity measurements is +0.02 logarithmic units.
2. The sulfur fugacity sensor is also designed as electrochemical cell with platinum internal and external electrodes, Ag0 as a reference buffer, Ag+ ion-conducting (Na,Ag)Al2O3 ceramics, and external Ag2S fixing Ag potential (Fig.2c) [1].
3. The activity of chlorine is measured by electrochemical cell consisting of external and internal Pt-electrodes, reference buffer NaxWO3, Nasicon (Na3Zr2Si2O12P) ceramics, conducting Na+ ion, and external NaCl compound fixing Na potential (Fig. 2).
4. Natural electric potential between hot fumarole and cold sulfur cover is measured by platinum plate electrodes.
All pressure transducers, cold thermocouple junctions, and analog transformer are fitted with thermoelements 1019EM1, that allows to account for the appropriate temperature corrections in automatic operation. All devices are hermetically sealed and may be applied in aggressive volcanic gas conditions for a long time. The temperature calibration in the laboratory conditions was performed for the thermocouples, pressure transducers and overall system. The pressure transducers were also calibrated against U-shaped water manometer. Hydrogen sensor was tested in the laboratory at temperature 800oC and pressure 1 bar in equilibrium with the Ni-NiO-H2O and Co-CoO-H2O buffers; oxygen sensor was tested in equilibrium with MnO2-Mn2O3 buffer, and chlorine sensor in equilibrium with Ag-AgCl. The described above technique was successfully applied at Kudriavy volcano [2]
Fig.2 Principal schemes of sensing devices: (a) partial hydrogen pressure sensor; (b) double cell for the measurements of excess gas pressure in volcanic channel and atmospheric pressure c) electrochemical sensors for the measurements of sulfur and chlorine fugacities in gas. a-cell for measurements of partial hydrogen pressure in gas; b- double cell for measurements of gas pressure in fumarole vent and atmospheric pressures; c- electrochemical sensors for measurements sulfur and chlorine fugacity in gas. 1-pressure transducers; 2-steel stainless capillary; 3-Pt-membranes; 4-protactions membranes; 5-silicon tube; 6-quartz tube; 7,8- inside and outside buffer (Ag-for S-sensor, NaxWO3- for Cl-sensor); 10-ion conducted ceramic (b-(Na,Ag)Al2O3 -for S-sensor, nasicon -for Cl-sensor)).
Reference:
Pivovarov S.A. Cadmium adsorption on ferric iron oxide.
Under natural conditions the adsorption processes fully control the behaviour of trace elements dictating their low natural level. So, oceanic waters are undersaturated with cadmium carbonate by approximately 250000 times. Ferric iron oxides, due to their abundance and high sorption ability, are the most important natural adsorbents. Therefore, a study of their adsorption properties is particularly important for understanding of geochemical cycles of trace elements in the zone of hypergenesis .
A detailed experimental study of cadmium adsorption on hematite has shown the following specific features of cadmium behaviour;
-each cadmium ion interacts with two acidic functional surface groups ( the value of surface concentration acidic functional groups is 7.0-7.6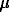 
mole/m2 whereas the value of maximum cadmium adsorption is 3.8 6 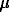mole/m2 at temperatures 25-100oC).
-cadmium adsorption is described by the mass law; the earlier observed deviations from the mass low at low adsorption densities were due to the effect of atmospheric carbon dioxide impurity. The equilibrium:
2=AH + Cd2+ = (=A)2Cd + 2H+; logKo = log[q Cd/q 2=AH] - log[Cd2+] + 2log[H+];
logKo = -11.5 (25oC), -10.1 (60oC), -8.6 (100oC).
(θ is the ratio of the surface concentration to the total number of acidic functional groups on the hematite surface, 7.6 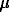mole/m2; the constant values are corrected to zero ionic strength).
-Temperature dependence of the cadmium adsorption constant in the range of 25-100oC shows that the enthalpy of this reaction (82 kJ/mole) is quite close to the enthalpy of cadmium hydroxide precipitation (88 kJ/mole). That is a very important correlation for an estimation of the adsorption constants at temperatures other than room temperature.
-It has been found that the main contribution to cadmium adsorption under natural conditions is made by an equilibrium with the formation of cadmium carbonate complex
72
=AH + =BOH + Cd2+ + CO2 = (=B)CO3 . (=A)Cd + 2H+
logKo = log[q
Cd/(q
=AH.q
=BOÍ)]-log[Cd2+]--log[CO2,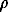 
-]+2log[H+]; logKo = -3.8 (25oC)
Fig.1. Effect of temperature and carbon dioxide concentration on the sorption of cadmium on hematite. Conditions: ionic force 0.002 M, specific surface of hematite 6 m2/g; O: 25oC, total cadmium concentration is 0.26 mM, hematite 41 g/l/ argon medium; ●: 25oC, total cadmium concentration is 0.11 mM, hematite 47 g/l. carbon dioxide pressure above the solution is 0.35 m Atm; □: 60oC, total Cd concentration is 0.37 mM, hematite 34 g/l, argon, ♦: 100oC, total Cd concentration is 0.47mM, hematite 32 g/l, argon
Lakshtanov L.Z., Karasyova O.N., Ivanova L.I. Strontium sorption on hematite at elevated temperatures
Sorption onto iron hydrous oxide surfaces strongly controls the mobility of many trace metals in sediments and soils. To the most dangerous radioactive substances belongs 90Sr formed in nuclear reactions of the uranium fission.
We have used the experimental method representing a combination of acid-base potentiometric titrations with metal adsorption data to create a thermodynamic model for the heterophaseous system hematite (=FeOH) H+ - Sr2+ depending on p[H+] and sorbate/sorbent (Sr2+/=FeOH) ratio at 25, 50, and 75oC.
In the evaluation of experimental data, the Extended Constant Capacitance Model (Nilsson, 1995) has been used. Optimization of model parameters was performed via the nonlinear least square optimization program FITEQL 3.1 (Herbelin and Westall, 1994).
The best fit to the experimental data could be obtained by a model consisting of two surface complexes with the overall stoichiometries which can be interpreted as formation of a series of inner-sphere monodentate complexes according to the following equilibria:
=FeOH + Sr2+ Û =FeOHSr2+ and =FeOH + Sr2+ + H2O Û =FeOSrOH + 2H+.
The corresponding intrinsic equilibrium constants were calculated for 25, 50, and 75oC.
Sr adsorption enthalpies are 48 and 147 kJ/mole for =FeOHSr2+ and =FeOSrOH respectively. The difference between these values is caused by coadsorption of two hydroxide-ions. This also confirms a conclusion obtained from the fitting of experimental data that Sr adsorbs onto the hematite surface in a similar inner-sphere manner independent on pH. Moreover, this is confirmed by the entropy of =FeOHSr2+ formation (196 J/K mole) which is to be related to the dehydration of Sr2+. This value is very close to the entropy of hydration of Sr2+ ions in aqueous solutions amounts -205 J/K mole. It can be inferred that nearly the whole hydration entropy was gained when Sr adsorbs.
The combined effect of the pHpzc decrease and the positive enthalpies of surface complexes formation is to favor Sr adsorption on hematite at enhanced temperatures (fig.1). Sr adsorption and retardation in the natural aquatic environment is unlikely at ambient T and pH, but may be significant in the radioactive waste disposal at elevated temperatures.
Fig.1. Predominance area diagram for Sr(II), calculated for the system hematite (=FeOH) H+ - Sr2+, [=FeOH]tot = 2 mM (= 70 g hematite dm-3).
#Bondarenko G.V. and Gorbaty Yu.E. The integrated intensity of H2O stretching band at 350 and 500oC and in a wide range of densities
E-mail: hunch@issp.ac.ru, Fax: 7(095)52 46205
The most valuable feature of infrared absorption spectroscopy is the possibility to measure the absolute intensities of spectral bands. The integrated intensity of absorption gives important information on the inter- and intramolecular interactions in a substance and can readily be used for analytical purposes. In this paper, we describe shortly the results obtained with a new HTHP cell with changeable path length designed to study highly-absorbing
#The support from INTAS (Grant 96-1989) and the RFBR (Grants N 97-05-65956 and 99-05-65554) is greatly appreciated.
73
substances like water or carbon dioxide. In particular, the behaviour of the integrated intensities of the stretching vibrations of H2O at isothermal compression has been studied in a wide range of densities.. This quantity may be thought to be a measure of the probability of hydrogen bonding in water.
The spectra of the absorption coefficient of H2O have been obtained along two isotherms: the supercritical (500oC) and subcritical (350oC) in the pressure range from 150 to 1000 bar. This is a rather difficult experiment because to study water at high pressures very small path lengths, about a few microns, are needed, while deformations of all parts of the cell at high temperatures and the stress induced by pressure have a much greater values. The density of water in the study changed from approximately 0.048 to 0.76 g cm-3. Some examples of the spectra obtained at a constant temperature of 500oC are shown in Fig. 1.
Fig. 1. Some spectra obtained at 500oC
As may be seen, compression of water induces explicit changes in the complicated shape of the stretching band of H2O. The intensity of the band increases with the pressure rise due to the increase in the degree of hydrogen bonding.
The rotational branches of the spectra clearly seen at low density get masked by the enhanced intensity, so that at a pressure of 750 bar they cannot be distinguished. It has been shown, however, that if the intensity of a combination band does not depend on hydrogen bonding the 'embryos' of the rotational branches can be recognised more easily. The spectra of such a band indicate that at supercritical temperatures a significant part of molecules gains rotational freedom (2).
Fig. 2a. shows the integrated intensity of the band as a function of pressure. At pressures higher than 200 bar it is always lesser for 500oC than for 350oC in virtue of higher degree of hydrogen bonding at higher density and lower temperature. The discontinuity in the pressure trend for subcritical isotherm is caused by the liquid-gas transition. The same data are presented in Fig. 3b as a function of density. One can see that the integrated intensities depend on density of the water fluid practically linearly along both isotherms. However, the slopes of two isotherms are quite different. It is more steep for 350oC.
Comparing the data on the integrated intensity and frequency shift one can notice an interesting fact: the integrated intensity at 350oC depends on density more strongly than that at 500oC, while the behaviour of max is quite opposite. This fact does not agree with the well-established linear correlation between the integrated intensity and max for OH or OD of HDO that is valid for a wide range of temperatures and pressures. It is also clear that the integrated intensity of the stretching band is a far more sensitive characteristic of the probability of hydrogen bonding in liquid and supercritical water than the position of the band's maximum.
In this work we have also studied the effect of pressure on the integrated intensity of OD band of HDO up to 2000 bar. As has been found the integrated intensity and consequently the energy of hydrogen bonds decreases with the pressure rise despite the average shortest intermolecular separation in liquid water becomes smaller. The computer simulations of the compression of liquid water has shown that the reason for the ostensible contradiction is due to the bending of hydrogen bonds.
Fig.2. a) the pressure dependence of the integrated intensity; b) the integrated intensity as a function of density. Lines are guides for the eye
References:
74