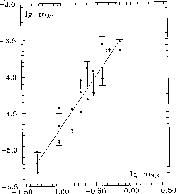
VI. Experimental study of sulfide equilibria and sulfide-forming fluid
(Leaders Dr. E.G.Osadchii, Dr. T.P.Dadze)
#Dadze T.P., Kashirtseva G.A., Akhmedzhanova G.M. Solubility of gold in the hydrogen sulfide in water solutions studied at T=300oC and P=300 atm.
Solubility of gold was experimentally studied at T=300oC and P=300 atm using a method of solubility of hydrogen sulfide in water solutions in the near-neutral region (pH=7.4). The hydrogen sulfide was given by thioacetamide, its concentration was varied from 0.05 to 1 mol/l. Gold was analyzed on an atomic-absorption spectrometer AAS1N in an air-acetylene flame at the wavelength 242.8 nm.
Fig.1. illustrates the experimental results in the co-ordinates lgmH2S-lg mAu. A clear dependence of gold solubility on concentration of hydrogen sulphide was obtained. At T=300oC this dependence is given by the simple equation:
lg mAu = -3.27197 + 1.45035∑lg mH2S + 0.17
The error was calculated by the least squares method, the calculation accounts for 87% of all the experimental points. Benning and Seward, 1994, mentioned that for the curve gold solubility Vs H2S content the factor of the slope equal to 1.5 is characteristic of the HAu(HS)o2 complex. The factor of the slope of our curve equal to 1.45 suggests that under our experimental conditions the dissolution of gold obeys the reaction:
Au + 2H2Saq = HAu(HS)o2 + 1/2H2aq.
The reaction constant calculated from our experimental data, lg k2 =-5.8+0.07 is close in value to those obtained by Hayashi, Ohmoto, 1991, lg k2= -5.15+0.36. Our experimental data on gold solubility in hydrogen-sulphide-containing solutions indicate that the concentration of gold in a solution grows with the concentration of hydrogen sulphide at mH2S = 0.05 mAu= 5∙10-6 mol/l, and at mH2S =1, mAu= 3.5∙10-4 mol/l. Such concentrations of gold in near-neutral hydrogen sulphide-containing solutions attest to the possibility of gold transport in hydrothermal solutions in the form of an uncharged hydrosulphide complex HAu(HS)o2 (T.P.Dadze, G.A. Kashirtseva, G.M.Akhmedzhanova).
Dadze T.P., Kashirtseva G.A., Orlov R.Yu. Solubility of Sb2S3 in 0.1-0.8 mol/l Na2S solutions at T=200oC.
# The work has been supported by the Russian Foundation for Basic Research, project N 96-05-64646
46
Solubility of Sb2S3 in 0.1-0.8 mol/l Na2S solutions was studied by a method of Raman spectroscopy at temperatures to 200oC. The main form of occurrence of Sb under the experimental condition was shown to be S:Sb=4:1 particle. It was reliably found for the first time that in strongly alkaline sulphide solutions (pH in excess of 12) the prevailing antimony complex is HxSbS4-(3-x) where antimony is in the pentavalent state. Characteristic vibration frequencies of the group S-Sb >> 370 cm-1 and those of H-S >> 2550 cm-1 (the vibration frequency of a free HS- group is 2574 cm-1).
References:
#Kotova A.A. and Osadchii E.G. A possibility of classification of ordinary chondrites based on fO2
The temperature dependences of oxygen fugacity were determined for several individual samples of ordinary chondrites belonging to different petrochemical types. The measurements were performed by using high-temperature galvanic cells in the temperature range 1000-1300 K. The following meteorites were studied: Okhansk (H4), Savchenskoe (LL4), Elenovka (L5), Vengerovo (H5), and Zhigailovka (LL6). All the samples are similar in phase composition and are composed of olivine (Mg,Fe)2SiO4, orthopyroxene (Mg,Fe)SiO3, kamasite a(Fe,Ni), tenite g(Fe,Ni), and troilite FeS. The stability fields of these phases in the Fe-Si-O-S system are shown in Fig. 1.
Fig.1. Stability diagram of the Fe-Si-O-S system at T = 1000 K. (1) FeSiO3 + Fe + 1/2O2 = Fe2SiO4 mineral abbreviations: tr -troilite, opx - orthopyroxene, ol - olivine, Fe - Fe-Ni solid solution.
The equilibrium
Opxss + Fe + 1/2O2 = Olss (1)
is affected by only oxygen fugacity. All the solid phases involved in this reaction are solid solutions. At constant pressure, the oxygen fugacity is determined by temperature and activities of components of the solid solutions:
logfO2 = 2K(1) + 2(log aolFa - log aopxFs - log assFe) (2)
where K(1) is the constant of equilibrium (1), aolFa is the Fe2SiO4 activity in olivine, aopxFs is the FeSiO3 activity in orthopyroxene, and assFe is the Fe activity in the iron-nickel solid solution.
All the types of ordinary chondrites differ significantly in the composition of the coexisting solid solutions. If the system is closed, fO2 only depends on temperature and composition of these phases. Thus, the equilibrium fO2 values can be used as numerical criteria for chondrite classification.
The oxygen fugacity in ordinary chondrites (fO2) was measured relative to that in air (fO2*) with a one-tube (simple) electrochemical cell based on Y2O3-stabilized zirconia (YSZ) as a solid electrolyte with O2--conductivity:
Pt, fO2, meteorite sample |YSZ|f*O2 (air), Pt (A)
The resulting temperature dependences of the equilibrium EMF values obtained (E, mV) are described by the following equations:
E (Okhansk H4) = -14.08685.T + 1.80984.T.l n.T + 553.9685 (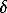 =+0.99; 1070<T(K)<1270);
=+0.99; 1070<T(K)<1270);
E (Savchenskoe LL4) = -4.5933.T + 0.64404.T.lnT + 882.719 (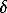 =+0.99; 1070<T(K)<1270);
=+0.99; 1070<T(K)<1270);
E (Vengerovo H5) = -29.8333.T + 3.75838.TlnT +2849.89 (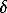 =+0.99; 1050<T(K)<1230);
=+0.99; 1050<T(K)<1230);
E ( Elenovka L5) = -5.33135.T + 0.6075.lnT +21 28.6 (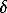 =+0.98; 1050<T(K)<1230);
=+0.98; 1050<T(K)<1230);
E ( Zhigailovka LL6) = -1.3285.T + 0.113.TlnT + 1581.72 (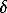 =+0.98; 1050<T(K)<1230).
=+0.98; 1050<T(K)<1230).
The following equation shows the relationship between the EMF of Cell (A) and oxygen fugacities in the sample (fO2) and reference (fO2*) systems:
logfO2 = logf*O2 - nFE10-3/RTln10 (3)
where n is the number of electrons transferred in the reversible electrochemical reaction O2 + 4e - O2- on platinum electrodes (n=4); F is the Faraday constant (96484.56 C/mol); E is EMF; R is gas constant (8.31441 J. mol-1.K-1); T is absolute temperature (K), fO2* is the oxygen fugacity in the air (logfO2*=-0.6789).
The temperature dependences of fO2 of all studied ordinary chondrites are described by the following equations:
lgfO2 (Okhansk) = -31256.4/T(K) + 10.7 (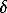 =+0.97; 1070<T(K)<1270)
=+0.97; 1070<T(K)<1270)
lgfO2 (Vengerovo) = -28722.8/T(K) +8.2 (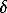 =+0.99; 1050<T(K)<1230)
=+0.99; 1050<T(K)<1230)
lgfO2 (Elenovka) =-30068.0/T(K) + 9.7 (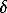 =+0.98; 1050<T(K)<1230)
=+0.98; 1050<T(K)<1230)
lgfO2 . (Savchenskoe) = -32903.1/T(K) +12.7 (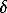 =+0.97; 1070<T(K)<1270)
=+0.97; 1070<T(K)<1270)
lgfO2 (Zhigailovka ) = -29311 .1/T(K) + 9.153 (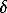 =+0.98; 1050<T(K)<1230)
=+0.98; 1050<T(K)<1230)
47
Fig. 2. LogfO2 of ordinary chondrites obtained in this study [Cell (A)] and by other authors. (1) Savchenskoe (LL4); (2) Zhigailovka (LL6); (3) Elenovka (L5); (4) Okhansk (H4); (5) Vengerovo (H5); (6) (Williams, 1970) for the average composition of H-chondrites; (7) (Brett and Sato, 1983) for Okhansk (H4).
The oxygen fugacity was found to increase from H-chondrites to LL-chondrites (Fig. 2) and decrease with increasing grade of metamorphism of chondrites within a single petrochemical type (H4, H5, etc.). These conclusions are consistent with Brett and Sato's data (1983).
Thus, the fO2 of ordinary chondrites were shown to be related to their chemical composition and grade of metamorphism. Therefore, fO2 measurements performed for a representative sampling of ordinary chondrites (about 30 samples of different petrochemical types) can serve as the basis for their quantitative classification.
References :
#Osadchii E.G., Fedkin M.V., and Lunin S.E. Thermodynamic properties and a phase transition in the sphalerite solid solution (Fe,Zn)S.
The previous study of FeS activities in sphalerite solid solution (sp) by the solid-state galvanic cell technique [1] revealed breaks of the temperature dependence of aFeSsp within the temperature range 950-1000 K. These phenomena were investigated in more detail in the cells:
Pt,FeS(in sp),Fe3O4,Ag,Ag2S |YSZ| Ni,NiO,Pt (A)
Pt,FeS,Fe3O4,Ag,Ag2S |YSZ| Ni,NiO,Pt (B)
Pt,ZnS(in sp),ZnO,Ag,Ag2S |YSZ| ZnS,ZnO,Ag,Ag2S,Pt (C)
The obtained emf data made it possible to determine the free energy of mixing (GM) of Fe0.1Zn0.9S and reveal some specific features of the emf curves in the temperature range where the sphalerite anomalies were observed.
Free energy of mixing of Fe0.1Zn0.9S. The temperature dependence of aFeSsp was determined from the difference in emf values (E) between Cells (A) and (B):  E = E(A) - E(B). In this procedure, the potential of the reference system Ni-NiO is eliminated, and stoichiometric FeS is taken for the standard state (a=1). As a result, FeS and ZnS activities in sphalerite solid solution can be calculated through the equations:
E = E(A) - E(B). In this procedure, the potential of the reference system Ni-NiO is eliminated, and stoichiometric FeS is taken for the standard state (a=1). As a result, FeS and ZnS activities in sphalerite solid solution can be calculated through the equations:
lgaFeSsp = 8F10-3/3Rln10 .  E/T (1)
E/T (1)
lgaZnSsp = 2F10-3/Rln10 . E(C)/T (2)
where F=96484.56 C/mol -Faraday constant, R=8.31441 J/mol/K - gas constant, and E - emf (mV).
Fig.1. Temperature dependence of emf of Cell (A) and (B).
48
Different portions of the experimental curves E=f(T), which are denoted with letters in Fig. 1, were fitted separately as:
 E(ab)=0.086T-51.07 (900<T,K<995;
E(ab)=0.086T-51.07 (900<T,K<995; 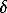 =1.5 mV) (3)
=1.5 mV) (3)
 E(b'c)=0.131T-106.85
E(b'c)=0.131T-106.85
(1009<T,K<1080; 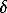 =1.5 mV) (4)
=1.5 mV) (4)
E(C)(ab)=-0.008T+6.43
(900<T,K<995; 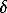 =0.1 mV) (5)
=0.1 mV) (5)
E(C)(b'c)=-0.009T+7.11
(1009<T,K<1060; 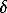 =0.1 mV) (6)
=0.1 mV) (6)
and for Cell (B):
E(B)=221.36-2.842T+0.3918TlnT
(780<T,K<1050, 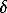 =1.3 mV) (7)
=1.3 mV) (7)
The Gibbs energy of mixing of sphalerite solid solution with 10 mol % FeS is determined as GM = RTln10(0.1.lgaFeS + 0.9.lgaZnS), where activities of the components can be calculated by substitution of Eqs. (3) and (4) into (1) and Eqs. (5) and (6) into (2). The total (GM), ideal (GI, at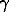 = 1), and excess (GEM) energies of mixing are shown in Fig.2. Within the whole temperature range studied, the sphalerite solid solution has a positive deviation from ideality:
= 1), and excess (GEM) energies of mixing are shown in Fig.2. Within the whole temperature range studied, the sphalerite solid solution has a positive deviation from ideality: 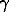 > 1, GI - GM = GEM > 0.
> 1, GI - GM = GEM > 0.
Fig. 2. Temperature dependence of the free energy of mixing of the sphalerite solid solution Fe0.1Zn0.9S.
Equation (1) can be corrected for FeS activity in pyrrhotite, which actually is not unity. Composition of pyrrhotite in equilibrium with Ag-Ag2S buffer and respective FeS activity were evaluated from [2] and [3]. In this case, a negative deviation from ideality of the sphalerite solid solution is possible at temperatures above 1100 K.
Phase transition. According to [4], pure ZnS exists in three structural modification: 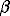 -cubic (T < 873 K),
-cubic (T < 873 K), 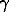 -rhombic (873 < T,K < 1293), and
-rhombic (873 < T,K < 1293), and 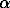 -hexagonal (T > 1293 K). If these properties hold for the Fe-sphalerite solid solution, points b and b can be considered related to the
-hexagonal (T > 1293 K). If these properties hold for the Fe-sphalerite solid solution, points b and b can be considered related to the 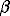 «
« 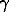 transition. Since -(¶
G/¶
T) = S, S(ab) = S(
transition. Since -(¶
G/¶
T) = S, S(ab) = S(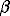 ) << S(bb), S(bc) = S(
) << S(bb), S(bc) = S(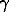 ) << S(bc) at any positive
) << S(bc) at any positive  T = T(b)-T(b) ¹
0. Therefore, the obtained dependences E=f(T), ai = f(T), GM = f(T), etc., which have the meaning of thermodynamic potential, indicate a possible thermal effect associated with this phase transition. However, differential thermal analysis did not confirm clearly the presence nor absence of the thermal effects in sphalerite solid solutions of various composition. Thus, the order of this phase transition can not be determined. The temperature of the supposed phase transition inversely depends on FeS content in sphalerite.
T = T(b)-T(b) ¹
0. Therefore, the obtained dependences E=f(T), ai = f(T), GM = f(T), etc., which have the meaning of thermodynamic potential, indicate a possible thermal effect associated with this phase transition. However, differential thermal analysis did not confirm clearly the presence nor absence of the thermal effects in sphalerite solid solutions of various composition. Thus, the order of this phase transition can not be determined. The temperature of the supposed phase transition inversely depends on FeS content in sphalerite.
Behavior of the function E = f(t) in the vicinity of the phase transition. The results of emf measurements in Cell (A) for the sphalerite Fe0.3Zn0.7S are shown in Fig. 3. The emf curves obtained on heating and cooling differ, have a complex shape, and coincide only between points b and b. Each of the curves has an extremum (¶ E/¶ T=0) and an inflection point (¶ E/¶ T = ¥ ). In the vicinity of the inflection points, the temperature dependence of emf is well described by the equation E = a + bT1/3.
Fig. 3. Temperature dependence of emf of Cell (A) obtained for the sphalerite solid solution Fe0.3Zn0.7S. Arrows down - cooling; arrows up - heating.
It is not well understood if the curve shape in Fig. 3 reflects an equilibrium state of the system. But it should be noted that the time interval between every two points was 48-100 hours, and the cell was let to stay in equilibrium at least for 12 hours. Temperature and emf were measured every 10 minutes, and all data were displayed at a monitor in the form of kinetic curves. It should be noted that the system reached equilibrium faster in the extremal range than in the gentle areas.
References:
49