Photochemical process
Velocity of photolysis products, km/s
Photolysis time, s
SO2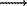 SO + O
SO + O
0.9
1.6
104
SO2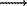 S + O
S + O
1.6
1.6
2 × 104
SO2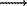 SO2+ + e
SO2+ + e
4.3
106
SO 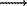 S + O
S + O
1.3
1.9
2 × 103
SO 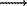 SO+ + e
SO+ + e
4.5
106
S 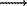 S + e
S + e
4.4
106
Physics of Earth
Berezhnoi A.A. About comet origin of lunar ice.
key words [ lunar ice comet]
A concept about the existence of the ice of comet origin in cold traps near the Moon poles was suggested in [2]. The radar experiment on board of the "Klementina" spacecraft above the south pole of the Moon found a material close to ice in radiolocation properties [7]. Comets are the most probable sources of ice on the Moon; therefore, the major amount of volatiles can be delivered to the Moon during comet showers [8]. Diffuse structures can be traces of the last comet shower that took place ts ~ 10 mln. years ago [10].
When the velocities of collisions between comets and the Moon are 10-60 km/s, the major portion of the kinetic energy of a comet is consumed to heating and melting of the Moon matter; therefore, the velocity of impact vapor scatter is substantially lower than the velocity of the collision of the comet with the Moon, and a considerable portion of the comet matter remains in the Lunar gravitational field.
When the Moon retains k1 ~ 0.1 of the comet mass (the mass of a medium comet is 1013 kg [4]), the pressure of the impact-formed atmosphere P ~ 10-7 bar and the concentration of molecules near the Lunar surface N0 ~ 1012 cm-3. As follows from the model concepts, the impact-formed Lunar atmosphere can be described by hydrodynamic laws, it is optically thin for UV radiation of the Sun, and hence, photolysis is an efficient mechanism of dissipation of this atmosphere.
Let us accept the lifetime of molecules in the Lunar exosphere to be t1 = tf, where tf is the lifetime of a molecule in the Solar radiation field relative to the photochemical process in an optically thin medium where dissociating particles gain the velocity exceeding the escape velocity for the Moon and leave the Lunar atmosphere. The lifetime of the Lunar atmosphere [1] t2~t1*N0/Nex, (1),where the density of particles in the exosphere Nex~108 cm-3. Substituting t1, N0, and Nex to formula (1), we obtain that t2 ~ 104tf (2).
Assuming that water (tf ~ 105 s [9]) is the main component of the Lunar atmosphere, the lifetime of this atmosphere t2 ~ 109 s ~ 300 years.
Let us evaluate the chemical composition of the Lunar atmosphere. The lunar matter contains no considerable amounts of volatiles; therefore, after condensation of the Lunar matter, the elemental composition and mass of gases retained by the Moon are determined by the matter of the comet origin. The elemental composition of the comet is accepted to be the same as that of Halley's comet [3]. Since t2 >> tf, the chemical composition of the Lunar atmosphere is determined by photochemical processes. The results of numerical calculations of the chemical composition of upper planet atmospheres can be accepted as the first approximation [6]. The main components of this atmosphere are H2O, CO, CO2, N2, and SO2. SO, S, traces of H2S, O2, NO, and HCN are also possible.
The components of the Lunar atmosphere can be divided into three classes: (1) condensing under conditions of the Lunar night and in cold traps, which are never irradiated by the Sun; (2) condensing in cold traps; and (3) noncondensing components. During the Lunar night, the surface temperature decreases to 100 K. The temperature of the Lunar surface in cold traps is theoretically estimated as Tp = 40 K [2]; according to the data in [7], the soil temperature in a cold trap at the depth of ~50 cm is 90 K.
Using the data on the condensation temperature of gases at different partial pressures [5], we obtain that at Tp = 90 K the condensation of S, H2O, SO2, CO2, and traces of HCN is thermodynamically possible in cold traps, while at Tp = 40 K gas hydrate CO, traces of H2S, NH3, CS2, COS, and NO are also condensed. The most favorable conditions for condensation in cold traps are formed for CO2. Although H2O dissipates rapidly, because it is the main component of the comet ice, the predomination of H2O in the Lunar ice should be expected.
Since the lifetime of the Lunar atmosphere t2 is comparable with the characteristic time of diffusion td at a distance of an order of magnitude of the Lunar radius and the t2/td ratio is independent of N0, a considerable portion of gases of the impact-formed Lunar atmosphere of 1 and 2 classes is condensed in cold traps.
Since the ice thickness on the Moon is not less than several decimeters [7], which is considerably greater than the increase in the ice thickness h ~ 1 cm upon the collision of the Moon with a comet, the formation of polar ice occurred during geological time intervals.
The study of the stratigraphy of the upper ice layers will give more comprehensive data on the periodicity and intensity of comet showers.
References:
76
Berezhnoi A.A.,(1) and Dorofeeva V.A. (2) The behavior of sulfur during impact interactions of comets with the Moon.
key words [ comet Moon sulphur](1) Shtenberg GAISh, Moscow State University, Moscow, Russia; @(2) V. I. Vernadskii Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences, Moscow, Russia
To explain radiolocation anomalies in polar regions of the Moon [1] and Mercury [2], it was assumed that their surfaces are covered with ice. Let us consider a possibility of inclusion of sulfur-containing compounds in the composition of these ices under assumption that comets are their main source.
The most probable velocity of collision of long-periodical comets with the Moon is ~40 km/s [3], and that of short-periodical comets is ~20 km/s [4]. The main parameters of the impact interaction of comets with the Lunar surface are presented in Table 1.
The elemental composition of the impact vapor (Table 2) was calculated as a mixture of substances of the Lunar crust [6] and the comet matter, whose elemental composition was accepted to be the same as that of Halley's comet [7].
After collision of a comet with the Moon, adiabatic scatter of the impact vapor formed occurs in vacuum. The equilibrium chemical composition upon the impact vapor scatter was studied for several variants of the initial conditions: T0 = 3000 K, P0 = 10-6, 10-3, and 1 bar.
In all variants considered, the main sulfur-containing compounds in the gas phase are SO2 at T > 1600 K, S2 at T = 1600-1300 K, and H2S at T < 1200 K. Sulfur was fixed in the solid phase at T ~ 1300-1200 K in the form of FeS. However, this reaction is likely kinetically inhibited, since the formation of FeS occurs due to the heterogeneous interaction of the gas phase with the previously condensed Fe or FeO. According to the estimation [8], the reactions in the gas phase are substantially retarded at T = 1500-1300 K. Thus, it is probable that the all comet sulfur is concentrated in the impact-formed atmosphere in the form of SO2, S2, and H2S.
Some SO2 and S2 molecules undergo photolysis to accumulate free sulfur in the Lunar atmosphere, because it is more difficult for sulfur atoms to overcome the gravitational force of the Moon (the escape velocity for the Moon is v2 = 2.4 km/s) than for oxygen atoms (see Table 3, time of photolysis [9]). For the Mercury, this mechanism of sulfur accumulation is not efficient due to the higher value v2 = 4.3 km/s.
Some portion of the sulfur and SO2 formed due to photochemical processes and perhaps H2S of the impact-formed Lunar atmosphere are condensed on the bottom of the Lunar craters, which are never irradiated by direct sun rays. Thus, the inclusion of sulfur-containing compounds in the composition of the Lunar ice seems to be quite probable.
References:
Table 1.
|
Vcomet |
% of total number of comets |
Total mass of impact vapor (estimated in [5]) |
Mass of retained impact vapor (estimated in [4]) |
% of comet matter in impact vapor
|
|
<15 |
15 |
1 |
0.5 |
100 |
|
15-20 |
45 |
2 |
1 |
50 |
|
20-30 |
30 |
3 |
1,5 |
20 |
|
>30 |
10 |
10 |
7 |
10 |
Table 2.
|
Element |
Elemental composition |
Composition of retained impact vapor for comets with velocities V, km/s; |
||||
|
Lunar crust |
comet |
<15 |
15-20 |
20-30 |
>30 |
|
|
Si |
3.33 |
1.86 |
1.86 |
2.80 |
3.15 |
3.26 |
|
Ca |
1.00 |
0.06 |
0.06 |
0.66 |
0.88 |
0.96 |
|
Al |
1.33 |
0.07 |
0.07 |
0.88 |
1.17 |
1.27 |
|
Mg |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
|
Fe |
0.66 |
0.53 |
0.53 |
0.61 |
0.64 |
0.65 |
|
O |
12.33 |
25.70 |
25.70 |
17.15 |
13.98 |
12.96 |
|
S |
0.03 |
0.72 |
0.72 |
0.28 |
0.12 |
0.06 |
|
C |
- |
11.48 |
11.48 |
4.14 |
1.42 |
0.54 |
|
H |
- |
77.63 |
77.63 |
28.01 |
9.60 |
3.63 |
77
Table 3.
|
Photochemical process |
Velocity of photolysis products, km/s |
Photolysis time, s |
|
|
SO2 |
0.9 |
1.6 |
104 |
|
SO2 |
1.6 |
1.6 |
2 × 104 |
|
SO2 |
4.3 |
106 |
|
|
SO |
1.3 |
1.9 |
2 × 103 |
|
SO |
4.5 |
106 |
|
|
S |
4.4 |
106 |
|
Kronrod V.A. and Kuskov O.L. Models of the internal structure of Galileo Satellites of the Jupiter and estimation of moments of inertia of the Europe and Kallisto.
key words [Jupiter satellite moment of inertia]
V. I. Vernadskii Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences, Moscow, Russia
The direct study of the Galileo satellites of the Jupiter (Io, Europe, Ganymede, and Kallisto) begun by spacecrafts of the "Pioner" and "Voyadzher" series was continued by the "Galileo" spacecraft (1989). The proceeding of the data of measurements of the gravitational fields of the Io and Ganymede made it possible to determine for the first time values of the dimensionless moment of inertia (I0 = I/MR2) of the Io [1] and Ganymede [2] and to suggest that these satellites have large metallic cores [1-3]. According to the models of formation of the Galileo satellites, a change in their chemical composition and average density with an increase in the distance from the central body is caused by the very high temperature of the proto-Jupiter surface (up to 5000 K), which prevents the ice condensation near internal satellites. However, at distance of the Europe, temperatures can be near the temperature of the water vapor condensation. Iron-stone cores of the Galileo satellites (silicate mantle plus metallic core) could be formed before the moment of the H2O ice condensation. After the temperature decrease in the gas-dust cloud (below the temperature of water vapor condensation), these cores were surrounded by a shell formed of accreted ice (variant of the heterogeneous accretion mechanism). Thus, it is assumed that all of the four satellites have iron-stone cores similar in composition and differ only by the thickness of the ice shell. It is noteworthy that the ice shell thickness for the Io is equal to zero [1, 3]. This assumption leads to equality of the average density and the dimensionless moment of inertia of all satellites without the ice shell.
The density of the ice shell of the Ganymede and other satellites (except the Io) to the H1 depth is accepted to be equal to the density of ice-1 (1 g/cm3); deeper, to the boundary with the iron-stone core (H2), to the density of ice-2 (1.2 g/cm3). The average density and the dimensionless moment of the iron-stone cores of the Ganymede and Io coincide at H1 = 70 km and H2 = 827 km. Based on this result, let us assume that
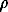 CK =
CK = 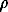 CG =
CG = 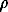 CE =
CE = 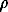 CI; ICK = ICG = ICE = ICI
CI; ICK = ICG = ICE = ICI
where 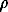 C and IC are the average density and reduced moment of inertia of the iron-stone core of the satellite; indices K, G, E, and I are attributed to the Kallisto, Ganymede, Europe, and Io, respectively. In this case, the radius of the iron-stone core RC and the moment of inertia IC can be unambiguously determined (Table 1).
C and IC are the average density and reduced moment of inertia of the iron-stone core of the satellite; indices K, G, E, and I are attributed to the Kallisto, Ganymede, Europe, and Io, respectively. In this case, the radius of the iron-stone core RC and the moment of inertia IC can be unambiguously determined (Table 1).
The content of the H2O ice in the satellites varies from the complete absence on the Io to 41-47 wt.% for the Ganymede and Kallisto. The shell of the Europe contains only 6% ice of the planet mass. It is likely that during the accretion period of the Galileo satellites the temperature of the ice condensation was in the vicinity of the Europe orbit. The results obtained make it possible to estimate the prognostic values of the dimensionless moment of inertia (I/MR2) of the Europe and Kallisto (italicized), Table 2.
Table 1. Parameters of iron-stone satellites of the Jupiter
|
Satellite |
|
IC |
RC, km |
H1, km |
H2, km |
M H2O |
MC |
|
Io |
3.529 |
0.378 |
1821 |
0 |
0 |
0 |
1 |
|
Europe |
3.529 |
0.378 |
1458 |
111 |
111 |
0.065 |
0.512 |
|
Ganymede |
3.529 |
0.378 |
1807 |
70 |
827 |
0.411 |
0.976 |
|
Kallisto |
3.529 |
0.378 |
1558 |
100 |
846 |
0.469 |
0.625 |
Note: MH2O is the water content in the planet, wt.%; MC is the ratio of the iron-stone core mass to the Io mass.
Table 2. Comparative parameters of satellites of the Earth and Jupiter
|
Satellite |
|
I/MR2 |
R, km |
|
|
Moon |
3.3437 |
0.3905+0.0023 |
1738 |
|
|
Io |
3.5294 |
0.378+0.007 |
1821.3 |
|
|
Europe |
3.03 |
0.346+0.007. |
1569 |
|
|
Ganymede |
1.936 |
0.3105+0.0028 |
2634 |
|
|
Kallisto |
1.81 |
0.311+0.007 |
2404 |
78
References :
Shapkin A.I. and Sidorov Yu.I. Evolution of the mineral composition of interstellar dust particles .
key words [interstellar dust]V. I. Vernadskii Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences, Moscow, Russia
The physicochemical evolution of the interstellar dust matter, which was a building material for the formation of the modern matter of planets and bodies of the Solar system, is the main problem of the modern cosmic chemistry. One of the construction methods for mathematical simulation of this evolution can be the apparatus of chemical thermodynamics, which allows one to calculate the equilibrium composition of chemical components in the system "matter of dust phase-gas of pre-planet cloud (PPC)" upon variation of P,T-conditions of this system.
The specific feature of natural systems (unlike chemical technological systems in which P,T-conditions are specified and controlled) is conditions of dynamic variations of P,T-parameters caused by the evolution of the system in the cosmic scale of space and time. Due to this, the use of isobaric-isothermal assumptions for calculations of equilibria in real systems, in the general case, is not substantiated. The P,T-conditions were different at each time moment and in each point of the PPC space, and the spatial chemical subsystem with constant pressure and temperature cannot be isolated in this system, which predetermines the use of the probability approach to solution of thermochemical problems [1].
The evaluations of the chemical composition and sizes of the interstellar dust particles are reduced to the situation that a particle (linear size ~1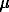 ) is the product of the gas condensation, whose total chemical composition is equivalent to the chemical composition of the star that gave birth to the matter of the protosolar nebula. These estimations agree with the previous model estimations [2] from the size of the particles of the gas condensate of the solar composition.
) is the product of the gas condensation, whose total chemical composition is equivalent to the chemical composition of the star that gave birth to the matter of the protosolar nebula. These estimations agree with the previous model estimations [2] from the size of the particles of the gas condensate of the solar composition.
Based on the studies of models of the matter evaporation at temperatures lower than the complete evaporation of iron-containing components, we can suggest a hypothesis that on heating the matter the Fe/Si ratio cannot decrease. Therefore, a sample of the extraterrestrial matter with the minimum Fe/Si ratio, the substance of the core of Halley's comet [3, 4], was chosen as the model composition of the interstellar dust matter.
Fig.1.
Fig.2.
Fig.3.
Figure 1 present the plots of changing the density of the nonevaporated portion of the starting particle (restite) heated under conditions of the equilibrium coexistence with the hydrogen atmosphere (curve 1) and the density of the equilibrium particle in the gas medium of the previously evaporated composition (curve 2). The estimated
79
density interval is typical of the matter of planets and satellites of the Solar system.
The probability approach to calculations of the equilibrium composition makes it possible to obtain plots of the temperature dependence of the probability of mineral phases in the equilibrium system. The statistical trends of the equilibrium coexistence of different mineral phases in the "dust particle-gas phase of PPC" system are presented in Figs. 2 and 3. The analysis of these trends helps to understand the sources of variety of the mineral compositions of samples of the extraterrestrial matter and explain the possibility of the equilibrium coexistence of mineral associates.
References:
Kronrod V.A. and Kuskov O.L. Evaluation of the temperature distribution in the lunar mantle.
key words [lunar mantle temperature distribution]V. I. Vernadskii Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences, Moscow, 117975 Russia
Data on the lunar temperature are few. According to the data of the "Apollon-15" and "Apollon-17" expeditions, estimations of the thermal flow are known only for two points of the lunar surface. In addition, the data on the electroconductivity and profiles of velocities of longitudinal and transverse wave distributions in the mantle are known. These data as well as the high quality of the lunar interior and the existence of mascons and deep-focused earthquakes give evidence that the temperature distribution in the mantle should be lower than the solidus temperature [1]. In the present work, we propose a method for the determination of the temperature profile in the lunar mantle from seismic data on velocities of longitudinal and transverse wave distributions in the mantle [2] on the basis of the derived restrictions on the content of the main ore-forming oxides [3, 4].
According to the seismic data [2], we consider the lunar mantle to consist of three zones (upper, middle, and bottom) with distinct boundaries and a jump of physical properties at depths of 270 and 500 km. The crust thickness is 58 km. The chemical and mineral compositions of the mantle are described by the CaO-FeO-MgO-Al2O3-SiO2 system (CFMAS). The absence of the density inversion over depth is assumed. The composition and physical properties were simulated by a THERMOSEISM program complex, which makes it possible to calculate the composition of a multicomponent mixture and its physical properties: velocities of volume waves, density, and other parameters.
Let us assume that the processes of the mantle differentiation to the upper, middle, and bottom zones resulted in the formation in each zone of the concentration profile of ore-forming oxides, which has the maximum uniformity over depth and a sharp change of the concentrations at depths of 270 and 500 km. In this case, the derivatives of the oxide concentrations with respect to depth in each zone of the mantle should satisfy the conditions:
¶
C/¶
H 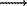 0, (C = FeO, MgO, Al2O3, CaO) (1)
0, (C = FeO, MgO, Al2O3, CaO) (1)
In addition, based on the results of the solution of the inverse problem on the reduction of the mantle composition [4], let us specify the restriction of the temperature at a depth of 270 km: T270 > 720oC.
It has been established that conditions (1) for the lunar mantle are satisfied when the dependence of the logarithm of temperature gradient on the depth is linear; therefore, the temperature profile is approximated by an exponential. It is noteworthy that although solutions with zero gradients of oxide concentrations all over the mantle exist, they imply very drastic conditions on the temperature profile. The temperature of 720oC at the depth of 270 km can be obtained only at T58 KM > 480oC. Therefore, we have found compromising solutions with zero concentration gradients at depths greater than 270 km, and at depths of 58-270 km: ¶
C/¶
H 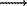 0, ¶
T/¶
H
0, ¶
T/¶
H 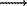 max. This solution provides a minimum temperature at the boundary between the mantle and crust when the restrictions of the seismic profiles in the mantle are fulfilled. The temperature profile obtained is considered to be optimum. The temperature value ranges as follows: 60 km, 430o-440o; 270 km, 720o-740o; 500 km, 920o-960o; and 1000 km, 1200o-1260oC. The typical profile is described by the equation:
max. This solution provides a minimum temperature at the boundary between the mantle and crust when the restrictions of the seismic profiles in the mantle are fulfilled. The temperature profile obtained is considered to be optimum. The temperature value ranges as follows: 60 km, 430o-440o; 270 km, 720o-740o; 500 km, 920o-960o; and 1000 km, 1200o-1260oC. The typical profile is described by the equation:
To(C) = 430 + 1050 × {1 - EXP[-0.0015*(H-58)]}
Profiles of the minimum (Tmin) and maximum (Tmax) temperatures can be determined from the restrictions of the minimum temperature in the middle mantle and the maximum temperature in the bottom mantle (at 1000 km, the temperature is somewhat lower than the solidus temperature):
Tomin(C) = 390 + 750 × {1 - EXP[-0.00275*(H-58)]}
Tomax(C) = 480 + 1450 × {1-EXP[-0.00125*(H-58)]}
References:
80