Hydrothermal processes, fluid system,
metasomatism
Konnikov E.G. Effect of water on the melting temperature of pyrrhotite: experimental data.
key words [pyrhotite melt water experiment]
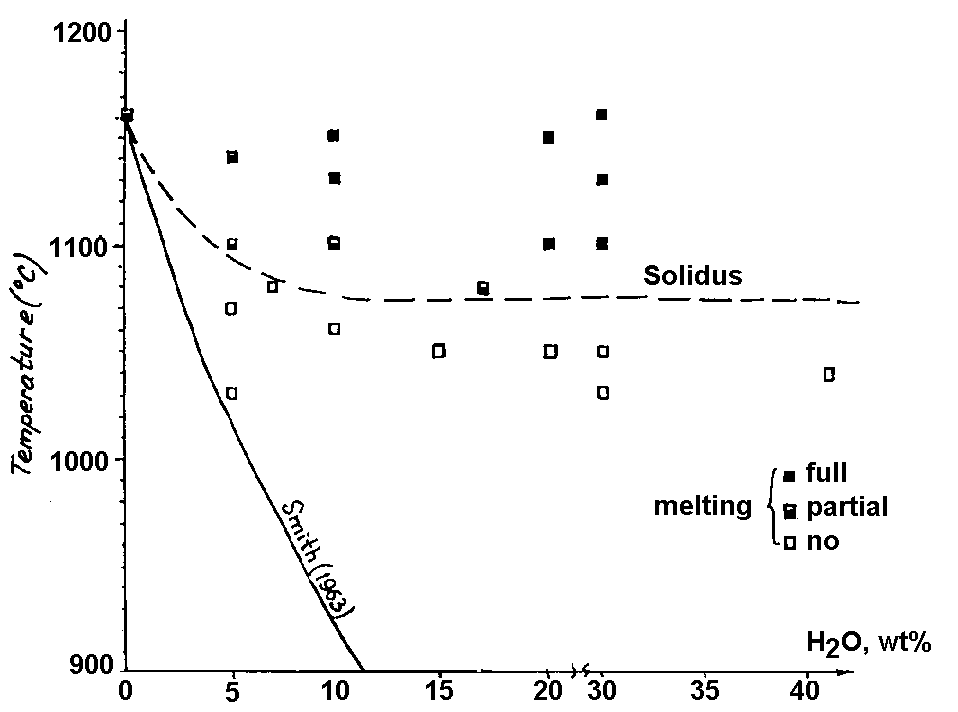
It is a common knowledge that fluid components participate in the formation of sulfide Cu-Ni deposits. This idea is supported by the occurrence of OH-, Cl, F-bearing minerals around sulfide drops (Genkin et al, 1979), of phlogopite and amphibole aureoles in the vicinity of massive ore deposits (Polferov, 1966; Hutchison and Robertson, 1972), of euhedral inclusions of these silicates in sulfides (Konnikov et al to be published). However, the investigations concerned with sulfide melts are scarce. This problem was first considered in the work by F.G.Smith (1963) where he reported the calculated data on the effect of water on the solidus temperature of pyrrhotite under the condition of its unlimited solubility in a sulfide liquid. According to these calculations the addition of 10 wt% water to pyrrhotite of the composition Fe0.92S leads to a decrease of its initial melting temperature by approximately 300oC. Later Naldrett and Richardson, 1967, who were concerned with the pyrrhotite-magnetite-water system showed by their experiments that H2O affects only insignificantly the melting temperature of pyrrhotite-magnetite mixtures under the experimental PT conditions (2 kb and 1010-1040oC). Meanwhile the calculations of F.G.Smith concerned with the influence of water on the solidus temperature of pyrrhotite remained unverified. We have carried out 19 runs on melting of pyrrhotite (Fe0.94S) with water at Ptot ~ P H2O =1 kb and T=1000-1160oC. The content of the water in the system varied from 5 to 41 wt%, the duration of the runs was half an hour or an hour, fO2 was controlled with an NNO buffer during the runs. The results are given on the diagram (Fig.1) where the experimental curve of the pyrrhotite solidus is compared with the curve calculated by F.G.Smith. These curves are seen to differ strongly from one another, that proves the invalidity of F.G.Smith's suggestion about the unlimited solubility in the pyrrhotite-water system. According to our experimental data, the solidus temperature of pyrrhotite drops only in the 10% range of water concentrations in a sulfide melt, remaining constant further on. So, the maximum of the water solubility in a pyrrhotite liquid is no greater than these 10 wt%. The decrease of the temperature of the onset of the pyrrhotite melting in the water of these concentrations does not exceed 80-90oC. These data disagree with the theoretical estimations of F.G.Smith.
27
Fig.1. Melting diagram of Fe0.94S-H2O system under Ptot ~ P H2O.
The examination of the experimental products have revealed very fine granophyre-like intergrowths of pyrrhotite and magnetite which fill interstitial pores between unmelted pyrrhotite grains. These intergrowths formed upon quenching of the liquid phase and are very much like the ones described by A.Naldrett, 1969. The occurrence of magnetite uniquely in products of pyrrhotite melting evidence for the dissolution of water in a sulfide liquid as this mineral could form only due to oxidation of a Fe ion in a pyrrhotite melt by the oxygen of the water. Interestingly, that no magnetite was found in the unmelted pyrrhotite either by X-ray phase analysis or petrographically.
References:
Ryadchikov A.P. , Osadchii E.G. Solubility of herzenbergite (SnS) and the complex formation Sn (II) in acidic chloride water solutions at 20-400oC.
key words [herzenbergite solubility hydrothermal conditions]
The forms of transfer and the mechanism of tin deposition at moderate-and low-temperature stages of the hydrothermal process as well as stoichiometry and thermodynamic properties of complex compounds Sn(II) existing at increased parameters in chloride hydrogen sulphide-containing solutions have been studied in this work. We examined the solubility of SnS in HCl-H2O solutions. To 230oC the studies were performed under a pressure of saturated water vapour in quartz capsules. The concentrations of tin in solutions under the experimental conditions were directly determined by a method of radioactive labels (Sn-113, or Sn-113 and Sb-125). At 300 and 400oC the runs were performed at 1 kb in titanium autoclaves, Sn was determined in 'quench` solutions.
The ionic mean (stoichiometric) activity coefficient of HCl solutions was calculated as a function of temperature (oC) using the quadratic function lg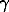 +=ao+bt+ct2, and the concentration (m-mole/kg H2O) dependence of the coefficients obeyed the equations:
+=ao+bt+ct2, and the concentration (m-mole/kg H2O) dependence of the coefficients obeyed the equations:
ao=(8.658m2 - 5.927m - 10.201)× 10-2, (1.0>m>0.1);
ao=(1.105m2 + 7.415m - 15.990)× 10-2, (m>1.0);
b=-(4.7116m + 1.5015)× 10-4 (m>0.1);
c=-(1.1628m + 1.0585)× 10-6 (m>0.1);
Fig.1. Temperature dependence of solubility of herzenbergite SnS in HCl-H2O solutions (dots - experimental data: 20-220oC under the saturated water vapor pressure: 300 and 400oC under 1 kb).
Fig.1 illustrates the temperature dependence of solubility of SnS in 0,10-1.28 m HCl solutions at 20-400oC
28
(in the co-ordinates lgmSn-inverse temperature). The curves are sinusoidal in form (conjugated parabolas) with two extrema and several points of the temperature transition. The solubility maximum of tin in 0.35-0.51 m HCl at 225oC shifts with the growing HCl concentration forwards lower temperatures down to 100oC in 3.20 m HCl. The second extremum (solubility minimum of SnS) is seen in 0.51-1.02 m HCl at T» 350oC. Its position depends on the concentration of HCl and, possibly, on the pressure. Similar is the course of the solubility curves of SnS at various temperatures depending on the HCl concentration as well (in co-ordinates lgmSn-lgmHCl).
The thermodynamic analysis of solubility of SnS has shown that in 0.1 m HCl at 20-125oC and in 1.28 HCl at 25-50oC tin is contained as Sn2+(aq) ion. Sn2+ also dominates in 0.35 m HCl at 100-125oC , in 0.51 mHCl at 300oC, and in 1.02 m HCl at 400oC. In the range 0.35-1.28 m HCl at 25-300oC the hydrolysis of SnS proceeds with the formation, along with Sn2+ and H2So, of chloride (SnCln2-n) and chlor-hydroxide (SnClOHo) water complexes Sn (II). The points of extremum (maximum) solubility of SnS in HCl solutions (at 25oC and pH 0.25+0.01; at 125oC and pH 0.33+0.03; at 225oC and pH 0.65+0.05) correspond to extremum states of Sn (II) at which there exist equalities of concentrations and charges between the oppositely charged (cation and anion) forms of bivalent tin (SnCln2-n), in conformity with 'isoelectric' ratios of stepped dissociation constants (and joint formation constants) of chloride forms of tin (SnCln2-n): k1/k2=k3/k4 (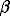 1/
1/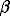 2=
2=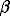 3/
3/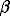 4), and others. The equality data are based on proportion retainment in the ratios of stepped constants as the charges of cation and anion forms change by unity. For the dissolution reactions of SnS in HCl-H2O proceeding with the formation of ion and chloride complexes of bivalent tin SnScrit +2H+ + nCl- = SnCln2-n +H2So the temperature dependencies (ToK) of the thermodynamic equilibrium constants(n=0-4) were obtained:
4), and others. The equality data are based on proportion retainment in the ratios of stepped constants as the charges of cation and anion forms change by unity. For the dissolution reactions of SnS in HCl-H2O proceeding with the formation of ion and chloride complexes of bivalent tin SnScrit +2H+ + nCl- = SnCln2-n +H2So the temperature dependencies (ToK) of the thermodynamic equilibrium constants(n=0-4) were obtained:
lgKo = -3087.4/T + 1.551;
lgKI = -73.1274 + 26.5019 × lgT;
lgKII = -16.331 + 0.0319726 × T;
lgKIII = -28.0306 + 0.092235 × T - 73.3275 × 10-6 × T2;
lgKIV = -3087.4/T + 91.7446 - 53.0038 ×
lgT +
+0.1845 ×
T - 146.655 ×
10-6 ×
T2.
For the reaction with the SnS hydrolysis which proceeds with the formation of chlor-hydroxide water complex, SnScrit + H+ +Cl- + H2O = SnClOHo + H2So , the temperature dependence of the thermodynamic constant has the form:
lgK* =-56.093 +19.4947 × lgT + 0.0037472 × T.
From these equations one can easily obtain the temperature dependencies for the other 12 intermediate reactions of chloride complex formation of Sn (II), including for 5 reactions of water hydrolysis of the ion and tin chlorides (SnCln2-n) proceeding with the formation of chlor-hydroxide (SnClOHo).
# Malinin S.D., Kurovskaya N.A. Equilibria of minerals with heterogeneous super-critical aqueous salt fluids.
key words [super critical aqueous salt fluid]Vernadsky Institute of Geochemistry and Analytical Chemistry
Among the specific features of fluid-mineral equilibria is the effect of increase (up to an order of magnitude) of the solvent action of fluids upon their heterogenization-separation into two phases: low-and high-concentrated ones with respect to the salt component which can be a result, e.g., of a pressure decrease in the system.
Fig. CaF2 solubility in chloride aqueous solutions. 1 -2m NaCl, 2- 1m NaCl-1mCaCl2 , 3-2m CaCl2 . Vertical line-boundary of NaCl heterogeneous region.
This effect was found by the authors for the CaF2-H2O-NaCl and CaWO4-H2O-NaCl systems [1]. It can be accounted for by the strong dependence of the solubility of a mineral (crystalline phase, in general) on the concentration of the dissolved electrolyte which is often characteristic of the fluid state. It was shown ibid. That the observable jump of solubility can be described by the law of lever with a satisfactory approximation. In the parameters, T,P, and the electrolyte concentration the jump agrees well with the instant of heterogenization of the NaCl-H2O system, from the data of [2].
The recent studies of this effect for CaF2 in equilibrium with the solutions of mixed NaCl-CaCl2 (1:1) composition and the individual CaCl2 solution have shown that in the mixed solutions the effect diminishes and is completely 'diffuse' in the CaCl2 solutions (fig.)
# The work has been supported by the Russian Foundation for Basic Research, project N 97-05-64036
29
Such a behavior of the system in the presence of CaCl2 is caused by a strong hydrolysis of CaCl2 solutions in the layered state under the experimental parameters due to the effect of 'dissipation' of the hydrolysis product-HCl-between the phases.
On the contrary, the hydrolytic effect of NaCl solutions with the same parameters seems to be insignificant.
The increase (jump) of solubility of the crystalline phases can stem from not only heterogenization of the supercritical fluid, but other processes as well if they bring about the concentration of the initial salt solution. Such a nature has, for example, the paradox, at first glance, effect of increasing solubility of the crystalline phase with the decreasing degree of filling the autoclave with a salt solution of the same initial concentration in the CaCO3-K2CO3-H2O system [3]. In this case the effect manifests itself at subcritical parameters as well. The principal condition of manifestation of such effect must be a strong dependence of the solubility on the concentration of the salt component sufficient for its 'being ahead' of the opposite effect on the solubility rendered by the water transition from the salt phase into the growing volume of the vapor phase (depleted in the salt component).
Finally, an increase of the solubility can result from loss of the water under the open system conditions (evaporation of the solution) [4].
As a whole, the effect considered must be of great significance for the processes of nature hydrothermal mineral formation and for artificial synthesis of crystals.
References:
Rumyantsev V.N. Nature of layering in alkaline silicate solutions under the hydrothermal conditions.
key words [alkaline silicate solution layering]Institute of lithosphere, RAS, Moscow 109180 Staromonetinii 22
It is known that under the particular physical and chemical conditions at elevated temperatures and pressures alkaline silicate solutions get layered with the formation of two immiscible liquids having close values of the silicic modulus (Ms-SiO2/Na2O) but essentially (by more than an order of magnitude) differing in the silica concentration (Tuttle, Friedman, 1950; Butuzov, Bryatov , 1957; Ivanov, 1962; Ganeev, Rumyantsev, 1971, Valyashko, Kravchuk, 1977; Rumyantsev, 1995, and others). The nature of this phenomenon is still unclear. Allowing for the composition of silicate particles in true solutions with a rather low silica content ('light phase') and in the 'heavy phase' , and for the specific features of layering and the reaction abilities of silicate particles, the author substantiates the mechanism of association of silicate particles in true solutions and their further polymerization which lead to the formation of the 'heavy phase' and layering.
The ability of silicate particles to chemically interact and associate in true solutions is due to the occurrence in their composition of OH-groups (oxygen of the silanol bond Si-OH possesses the electron donor properties owing to the presence of a free electron pair) and dipole formations O-Na+ wherein a sodium atom acts as the electron acceptor. The association of silica particles in such solutions, starting with monomers Na2[(SiO2(OH)2)] formed upon dissolution of silica and being accomplished with the formation of tetramers Na2[(SiO2)4(OH)2)] with Ms =4 proceeds with splitting-off of NAOH as a low-molecular reaction product (polycondensation). The restricted evolution of the polycondensation process is possibly related with weakening of the ion-ion interactions as the size of the silicate particles grows (and hence the strength of the ionic field decreases) and they can no longer participate in such reactions.
Taking into account the closeness of the Ms values of the silicate particles in the co-existing true solution (Ms =2.5-2.8) and the 'heavy phase' (Ms =2.7-3.5) at a drastically increased silica concentration in the composition of the latter (50 wt % and higher), the character of the effect of temperature and density of the solution (pressure) on layering, the occurrence of a large amount of water in the heavy phase (20-35 wt%), and also the absolute values of the initial temperatures of layering (250-300oC in 1.5 m NaOH solutions, 160-200oC in more concentrated solutions) one can suggest that further association of silicate particles proceeds by way of their polymerization with the participation of H2O molecules (ion-dipole interactions). The possibility for monomeric water to participate in this process is ensured by the specific features of its structure and the increased capability of reaction. At usual temperatures the concentration of monomers H2O in an aqueous solution is very low. However, as the temperature increases, judging from the decrease of the dielectric permeability of water due to the break-down of hydrogen bonds between the molecules, it continuously grows (somewhat decreasing with the increasing pressure, and increasing with the growing concentration of the solution). At elevated temperatures the concentration of monomers H2O achieves a considerable value. So, as prompted by the data of IR-spectra of water vapors at 350oC and 158 kbar (the density is 0.1 g/cm3) 20+5 % of all the molecules are in the monomeric state [1]. Being free of hydrogen bonds with other molecules, the water molecule is capable, due to oxygen atom having two free electron pairs, of entering into the donor-acceptor interaction simultaneously with two sodium atoms-constituents of the neighboring silicate particles (electron acceptors) with the formation of a bridging bond between them.
Reference:
30
# Laptev Yu.V. , Pal'yanova G.A. Experimental and thermodynamic modelling of solubility of metallic silver in the systems H2O-NaCl-HCl and H2O-CO2-NaCl-HCl at 350oC.
key words [silver solubility hydrothermal fluid carbon dioxide]Institute of mineralogy and petrography SB Ras Novosibirsk
In order to understand a specific role of carbon dioxide in the geochemical migration of silver we have carried out first experiments and the concurrent computer thermodynamic modelling of dissolution of Agmet in low-acidic solutions NaCl+HCl with and without CO2 at T=350oC and P=0.7 kb. The results of the experiments and computations in chloride systems containing 10 m CO2 showed that silver solubility decreases compared to the one in the analogous non-CO2 solutions. Similar regularities were revealed in the previous theoretical works for tungsten [5], gold [9], lead [1] and were experimentally proved for gold [11] and AgCl [2].
Experimental and thermodynamic computation techniques. The experiments were run in an apparatus for hydrothermal investigations, the titanium version of which was designed by N.V.Kapustin and V.I.Sorokin, provided with the supplementary system of sampling of the fluid phase. The technique of a sequential sampling was used enabling a decrease of the CO2/H2O ratio in the fluid in the course of one run due to the volume compensation of the selected mixed phase (H2O-CO2-NaCl-HCl) by the original water-chloride solution. The reactor volume was 50 cm3 , the sample volume was 4 cm3. The concentration of CO2 in the sample was derived from the difference in the sample weight before and after the gas exhaust. The concentration of silver in the water phase of the samples was analyzed by the method of atomic adsorption in an HCl medium. The initial compositions of the solutions were: 1m NaCl with the HCl concentrations 0.0018 and 0.018 m. The concentration of CO2 was restricted to xCO2 = 0.15 (10 m) which corresponds to the solubility limit of carbon dioxide in the given NaCl solution and at the given TP-parameters [4,6].
Fig. Agmet solubility in water-chloride-carbon dioxide fluid containing 0.018 (1.3) and 0.0018 (2.4) mHCl at 350oC and 1 kb (0.7 kb in the experiments) depending on the concentration of CO2. molar fraction on calculated (1.2) and experimental data (3,4).
# The work has been supported by the RFBR, grant N 97-05-65252
Table. Isobaro-isothermal potentials of particles in water and water-carbon dioxide solution (with account of G solv) at T=350oC and P=1kb for the system Ag-NaCl-HCl-CO2-H2O
|
Particles |
G, kcal/mol
|
Source |
|||
|
w |
GT |
GT+Gsolv |
|||
|
Ag+ |
0.216 |
11.49 |
12.55 |
[7] |
|
|
AgCl |
-0.030 |
-29.10 |
-29.56 |
-'- |
|
|
AgCl2- |
0.9169 |
-65.56 |
-60.55 |
[2] |
|
|
AgCl32- |
2.5565 |
-95.37 |
-83.24 |
[7] |
|
|
AgCl43- |
4/3935 |
-126.60 |
-105.81 |
-'- |
|
|
AgOH |
- |
-29.63 |
-26.96 |
[8] |
|
|
Ag(OH)2- |
- |
-67.96 |
-53.77 |
[10] |
|
|
AgCO3- |
1.5829 |
-111.31 |
-103.55 |
[7] |
|
|
Ag(CO3)23- |
5.0992 |
-226.49 |
-201.48 |
[7] |
|
In the computations performed by the method of free energy minimization, in the system of the given composition (the program GBFLOW the electrostatic approach was supplementarily used). The approach is based on the account of the change of the dielectric permeability of the H2O-CO2 mixture [9]. The isobaro-isothermal potentials of Ag+, AgCl, AgCl32-, AgCl43-, AgCO3-, Ag(CO)23- and other particles of the solution of the system in question were taken from the database SUPCRT92[7], and for AgCl2- and HCl from [2]. As for the rest of the silver forms-AgOHo, Ag(OH)2-, for them G were calculated from the extrapolation equation in [3] using the constants cited in [8,10]. The isobaro-isothermal potentials of the dissolved forms of silver and the corrections for the solvation values calculated by us are listed in the table.
Experimental and thermodynamic modelling results.The first experimental data on the equilibrium concentrations of silver in mixed water-chloride-carbon di-
31
oxide fluid are given in the figure along with the results of thermodynamic calculations. Apparently, a satisfactory agreement between the experimental and thermodynamic data is observed only for 0.0018 m HCl version. At greater acidity of the solutions the experimental silver concentration data were systematically lower by lgmAg=0.4 (2.5 times) than the calculated ones. In all the cases, however, one can see a noticeable effect of the increase of xCO2 on the decrease of solubility of Agmet (by approximately 1.8 times in the investigated range of carbon dioxide concentrations). The lower 'experimental' solubility compared to the calculated one is likely to be ascribed to insufficient corrosion strength of titanium (reactor material) in more acidic media. The same as the redox reaction of silver dissolution Agmet+H+nCl-=AgClnn-1 +0.5 H2, the interaction of titanium with acidic solution leading to hydrogen release will hinder the dissolution of Agmet.
According to the thermodynamic calculations the decrease of silver solubility in the presence of CO2 ought to be regarded principally as a consequence of the association of ions Na+, Cl-, H+ to form NaCl and HCl. With 10 m CO2 this process leads to a decrease in the concentrations of the basic complex former, viz., ion Cl-, by approximately 20 times, and of the ion H+ by 10 times. The effect of these negative factors is in the inverse relationship with the effect of an increase of the constants of formation of chlorine complexes of silver. In particular, for the prevailing form, AgCl2-,the corresponding constant according to the reaction Ag++2Cl-=AgCl2- grows from lgK=4.84 to 8.34 in the presence of the maximum CO2 concentration.
The supplementary factor for an increase of the silver solubility, as suggested by the thermodynamic calculations, is a noticeable action of CO2 as oxidant leading to the formation of methane CH4 by the reaction: CO2+4H2 =CH4+2H2O. Due to the consumption of hydrogen by the methane formation reaction the concentration of H2 (sol) in the presence of CO2 decreases. So, as suggested by the results of the experiments and thermodynamic calculations the net effect of the decrease of solubility of Agmet in water-chloride-carbon dioxide solutions is due to the stronger depressing effect of the processes of association of H+, Cl-, and Na+ to form HCl and NaCl as compared with the analogous increase of the chemical stability of the reaction products-chlorine complexes of silver and consumption of hydrogen for the methane formation. The enrichment in methane of gas-liquid inclusions with carbon dioxide at the stages of hydrothermal ore formation under the low-sulphurous conditions can be regarded as an additional important criterion of possible deposition of metallic silver due to a drastic decrease of its solubility at the redox potential determining role of the buffer pair CO2/CH4.
References:
# Akinfiev N.*, Schott Jac.**, Zotov Al.***Thermodynamic description of equilibria in mixed fluids H2O-non polar gas in the wide range of temperatures (25-700oC) and pressures (1-500 bars).
key words[water non-polar gas equilibria description]
Natural fluids rich in dissolved non polar gases (CO2, N2, CH4) may feature rather unconventional physical-chemistry with comparison to the 'traditional' pure aqueous solutions. One of the main causes of difference is specified in the pronounced lowering of dielectric con-
# This study was supported by GOSKOMVUZ grant of 1996 and RFBR grant 97-05-65385
32
stant of the mixture because of non polar gas presence. In the present communication a method for account of this effect in mixed fluids on the complexes formation reactions as well as phase equilibria as a whole is proposed. The method is based on consistent account of solvation effects of every aqueous species, that in terms of the well known HKF equation of state[1] refers to the modification of its chemical potential because of the change of dielectric constant of the mixed solvent, 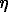 , compared to that of pure water,
, compared to that of pure water, 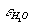
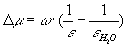
Here w =1.6603 × 105 Q2/re is the Born parameter of an ion with charge Q and electrostatic radius re. Having available the comprehensive thermodynamic database DPRONS92[2] that uses the HKF format, such an approach enables oneself not to confine within examination of isolated reactions, but study equilibria of the whole system.
Dielectric constant 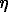 of the mixture with mole fractions c
H2O and xgas for H2O and the gas consequently was calculated with the use of Kirkwood equation:
of the mixture with mole fractions c
H2O and xgas for H2O and the gas consequently was calculated with the use of Kirkwood equation:
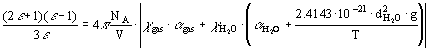
where however g-factor was calculated for pure water but using a value of whole volume V (but not the partial volume 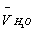 in the mixture)[3]. It is shown that this equation gives proper description of the available experimental data on the mixtures H2O-C6H6 and H2O-dioxane.
in the mixture)[3]. It is shown that this equation gives proper description of the available experimental data on the mixtures H2O-C6H6 and H2O-dioxane.
Volumetric properties of the mixtures were calculated on the base of Redlikh-Kwong equation of state. It is to note that Redlikh-Kwong parameter for H2O was restored at each pressure and temperature using PVT-properties of pure H2O on the base of 'exact' multiparametric equation of state[4].
Redlikh-Kwong parameters for pure gases were adopted from literature. The method, as well, includes the procedure for the computation of chemical potentials of the dissolved gases in a wide temperature (25-800oC), pressure (1-4000 bar), and concentration (xgas=0-0.6) range.
The validity of the general computation method was verified by processing the self made experiments on the AgCl solubility in the H2O-CO2-NaCl fluid at 400oC, 600 and 1000 bars and CO2 mole fractions up to 0.3 (fig.1).
Fig.1. Solubility of chlorargyrite AgCl in H2O-CO2 fluid plotted against mole fraction of CO2 at 400oC and pressures 600 and 1000 bars. Total NaCl concentration was equal 0.2 mol/kg H2O. Points represent the experimental values, lines are the calculated ones.
Fig.2. a) Portlandite Ca(OH)2 solubility in H2O-Ar mixtures (in terms of log molality of calcium) as a function of Ar mole fraction at 2000 bar 500oC. b) Calcite CaCO3 solubility in terms of log molality of calcium plotted as a function of CO2 mole fraction at 300oC, 1 kbar, and 4500C, 2 kbar. Solid curves are the computed solubility on the base of the proposed approach.
Handling the available literature experimental data on portlandite Ca(OH)2 and calcite CaCo3 solubilities in H2O-Ar [5] in H2O-Co2 [6] supercritical fluids enables to retrieve Born parameters for CaOH+ (w = -0.082ƒ105 cal/mol) and CaHCO3+ (w =0.0723· 105 cal/mol), and thus achieve adequate description of the experiment (fig.2).
The close agreement between experimental and calculated data proves possibilities of the proposed theoretical approach and gives a scope for computing complicated equilibria in mixed fluids.
References:
33
Pivovarov S.A. Adsorption of ions on the hematite surface.
key words [adsoption hematite cadmium]
The abstract presents new data on acid-base properties of hematite surface at 25, 60 and 100oC (Figs. 1-2), and on the adsorption of Cd2+ at 25 and 60oC (Fig. 3). A calculation method of adsorption equilibria is suggested.
The value of site density D of the hematite surface was determined at 3.8 moles/m2 based on the maximum adsorption of proton.
Apparently, the adsorption of cations and anions takes place on the different functional groups, and the term 'site' includes one cation- and one anion-exchange group.
The value of site density of oxide surface can be calculated by the following equation:
D = d/(4V), Å-2,
where d is lattice spacing (or average lattice spacing) for the face in question; V is volume per cation (the volume of the elementary cell, divided by the number of cations).
The calculated values of site density D for the oxides and hydroxides of Fe(III) (deviations are due to the variation in habit) are as follows:
Hematite - 3.4-3.8 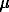 moles/m2
moles/m2
Goethite - 2.5-3.0 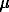 moles/m2
moles/m2
Lepidocrocite - 3.5 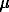 moles/m2
moles/m2
According to [3], D = 3.7 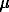 moles/m2 can be used for Fe(III) sub-amorphous hydroxides. This value corresponds (at usual specific surface about of 400 - 800 m2/g) to one site per 3-7 iron atoms in the hydroxide precipitates.
moles/m2 can be used for Fe(III) sub-amorphous hydroxides. This value corresponds (at usual specific surface about of 400 - 800 m2/g) to one site per 3-7 iron atoms in the hydroxide precipitates.
In NaCl solutions (0.01 - 1 m) the adsorption of protons and hydroxyl-ions is connected with the corresponding counter-ions by the stoichiometric relations:
H+ + Cl- = adsHClo (1)
Na+ + OH- = adsOHNao (2)
Fig.1. The difference between absorption of protons and hydroxyl-ions on the hematite surface in NaCl media at 25oC versus free molality of protons in solution.
Fig.2. The difference between absorption of protons and hydroxyl-ions on the hematite surface in 0.01 m NaCl at 25, 60 and 100oC versus free molality of protons and hydroxyl-ions in solution.
34
Fig.3. Adsorption of Cd2+ on the hematite surface (specific surface 6 m2/g); site density 3.8  moles/m2 ) versus free proton molality in solution. Temperatures, total concentrations of Cd2+ and sites D (moles/kg H2O) are indicated. Solid curves: X=0.5log[0.02Y/(1e-pD)-0.02e-pCd ×
Y]/(1-0.01Y)- 0.5 logK( Cd2+) + pKw +1.3(1-(1-(0.02e-pCd ×
Y/(1e-pD)0.5)2
moles/m2 ) versus free proton molality in solution. Temperatures, total concentrations of Cd2+ and sites D (moles/kg H2O) are indicated. Solid curves: X=0.5log[0.02Y/(1e-pD)-0.02e-pCd ×
Y]/(1-0.01Y)- 0.5 logK( Cd2+) + pKw +1.3(1-(1-(0.02e-pCd ×
Y/(1e-pD)0.5)2
logK(Cd2+, 25oC)=19.26; pKw (25oC) =13.97
logK(Cd2+, 60oC)=18.24; pKw (60oC) =12.98
These equilibria are practically temperature-independent (Fig.2). This directly shows the absence of energetic interactions. Thus, these reactions are essentially entropy-driven.
The standart entropy effects of these reactions decrease in direct proportion to the square root of the value of adsorption:
DS = DSor=0 - D2S( /D)0.5,
/D)0.5,
where DSor=0 is a standard entropy effect in the state of infinitely low adsorption; D2S is a change of standard entropy effect when the adsorption increases from infinitely low up to the maximum; Ã is adsorption; D is maximum mono-layer adsorption or site density.
For the reactions (1) and (2) within the entire temperature range (25-100oC) the following relations were obtained:
log[ HCl/(D-
HCl/(D- HCl)] -log[H+] -log[Cl-] = 9.5- 5.2(
HCl)] -log[H+] -log[Cl-] = 9.5- 5.2(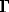 HCl/D)0.5 and
HCl/D)0.5 and
log[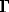 NaOH/(D-
NaOH/(D-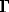 NaOH)]-log[Na+]-log[OH-] = 5.9-2.6(
NaOH)]-log[Na+]-log[OH-] = 5.9-2.6(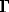 NaOH/D)0.5.
NaOH/D)0.5.
When bi-charged cations are adsorbed in mono-layer, two types of reactions take place:
1. Mono-dentate adsorption is characteristic of small cations with common co-ordination numbers in solutions equal to 4 and lower (Pb2+, Cu2+).
Me2+ + 2OH- = adsOHMeOH0
log[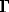 Me/(D-F)] - log[Me2+] - 2log[OH-] = logK -
Me/(D-F)] - log[Me2+] - 2log[OH-] = logK -
-2.6(F/D)0.5.
In the absence of competition F = 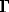 Me
Me
logK (Pb2+, 25oC) = 22.0 +0.2 [1,4]*
logK (Cu2+, 25 oC ) = 22.3 +0.3 [1]*
During the adsorption of Pb2+ on the surface of sub-amorphous iron hydroxide, as well as in the equilibrium with air, logK (Pb2+) can increase up to 22.8+0.4 [1,3]*, probably, because of partial oxidation up to tetra-valence state.
* The experimental data are used
2. Bi-dentate adsorption is characteristic of large cations with common co-ordination numbers of 6 and more (UO22+, Zn2+, Cd2+).
Me2+ + 2OH- = ads(OH)2Me0
log[2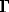 Me/(D-F)] -log[Me2+] -2log[OH-] = logK -2.6(1-(1-(F/D)0.5)2)
Me/(D-F)] -log[Me2+] -2log[OH-] = logK -2.6(1-(1-(F/D)0.5)2)
In the absence of competition F = 2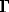 Me. Generally, in the solution of complex composition F = (S
Me. Generally, in the solution of complex composition F = (S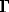 M1 + 2S
M1 + 2S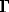 M2). Where M1 - Na+, Pb2+, Cu2+; M2 - UO22+, Zn2+, Cd2+.
M2). Where M1 - Na+, Pb2+, Cu2+; M2 - UO22+, Zn2+, Cd2+.
logK (UO22+, 25oC) = 23.0 +0.3 [2]*
logK (Zn2+, 25 oC ) = 20.2 +0.4 [1,3]*
logK (Cd2+, 25 oC) = 19.26 +0.2 [this work]
logK (Cd2+, 60oC) = 18.24 +0.1 [this work]
References:
# Togonidze V.V. Gold thio-complexes: quantum chemical calculations of structure, vibrational spectra and influence of solvatation.
key words [gold thio-complex calculation]Moscow Lomonosov State University,Geology Department, Mineralogy Division.
It is known that the most available part of world gold reserves is concentrated in massive sulphide and polymetallic ores. The research of oceanic bottom discovered among 'black smokers' deposits of massive sulphide type containing gold up to 70 ppm. Mineral composition of these bodies is investigated perfectly as distinct from the composition of hydrothermal solutions running out of mouth of smokers.
Modelling of natural hydrotermal solutions is limited so far by simplified systems. However, as we can see from experiment even in this case at high P and T sampling and further analysis cannot exclude serious errors.
Using Raman spectroscopy presented wide possibilities and new quantitative, and qualitative results were obtained even for the systems repeatedly studied.
Chloride gold compounds were studied earlier using Raman spectroscopy. In the case of gold sulphides, slightly soluble at normal conditions, we need to calculate ab initio vibrational frequencies and obtain at least qualitative estimate of Raman dispersion relative intensities.
The purpose of the present work is quantum chemical modelling of structure and vibrational spectra of gold thio-complexes at molecular and supermolecular level.
# Our research is supported by RFFI (Project 95-05-14560)
35
Table 1. Geometrical parameters of gold thio-complexes.
|
r(AuS) , Å |
r(SH) , Å r(S'H') , Å
|
<AuSH, o <AuS'H', o
|
|
|
Au(SH)2- + 4 H2O |
2.45 |
1.36 |
100.4 |
|
Au(SH)2- |
2.45 |
1.36 |
99.7 |
|
Au(SH)2-(SH2) AuS AuS' |
2.34 2.50 |
1.34 1.33 |
97.6 101.8 |
Table 2. Vibrational frequencies, IR absorbtion intensities.
|
Au(SH)2- |
Au(SH)2- +4 H2O |
Au(SH)2-(SH2 |
||||
|
Classification |
Frequency, cm-1 |
IR |
Frequency, cm-1 |
Classification |
Frequency, cm-1 |
IR |
|
def. |
91 |
0.24 |
86 |
tors. w , (S'H'H' rel. AuSH) |
75 |
0.036 |
|
def. |
92 |
0.20 |
87 |
def. |
80 |
0.0079 |
|
tors. w , (H-H) |
106 |
0.37 |
125 |
def. |
83 |
0.0016 |
|
val. |
274 |
0.00002 |
275 |
val. |
204 |
0.032 |
|
val. |
306 |
1.7 |
308 |
val. |
341 |
0.56 |
|
def. |
622 |
0.018 |
603 |
fan |
517 |
0.49 |
|
def. |
622 |
0.0014 |
641 |
fan |
563 |
0.028 |
|
val. |
2606 |
1.1 |
2639 |
def. |
717 |
0.0029 |
|
val. |
2606 |
0.85 |
2639 |
def. |
1324 |
0.052 |
|
val. |
2823 |
0.29 |
||||
|
val. |
2849 |
0.13 |
||||
|
val. |
2858 |
0.13 |
||||
Fig.1 Equilibrium geometry of Au(SH)2-
Fig.2 Equilibrium geometry of AuSH + 4 H2O
Fig.3 Equilibrium geometry of Au(SH)(SH)2
To calculate molecular parameters of gold thio-complexes we have chosen the SCF (self-consistent field) method (Hartree-Fock-Ruthan method) using relativistic pseudopotentials for a gold atom. It is demonstrated that this technique allows to reproduce literatural data for simpliest gold compounds.
Within the framework of this equilibrium geometrical parameters and vibrational frequensies of AuH, AuS, AuH3, AuH4-, AuSH, Au(SH)2+, Au(SH)2, Au(SH)2-, Au(SH)(SH2) complexes were predicted (Fig. 1-3, Tab. 1-2).
The influence of solvent (H2O) molecules on calculated geometrical and spectral parameters of thio-complexes of gold was investigated.
References:
36
#Shmonov V.M., Sretenskaya N.G., Vitovtova V.M. , Kotelnikov A.R. Electric conductivity of rocks as suggested by the data on the electric conductivity of rocks, the permeability and porosity of samples under elevated temperatures and pressures.
key words [electric conductivity Earth crust]
Magnetotelluric probing (MTP) is a direct method to investigate the present-day structure and fluid of the earth's crust and the upper mantle in situ. From the MTP data [1] the continental crust is two-layered: the resistance of the upper layer reaches 105 ohm × m, which indicates its extremely low permeability, and the electric conductivity of the middle crust is by several orders higher. It is implied that its lower layer is less dense, has a high permeability and porosity (on this basis forecasts are derived about great accumulations of oil and gas). W.F. Brace et al. [2] showed that the permeability of a sample is in good correlation with its electric conductivity that can be calculated using the data on the form of channels and electric conductivity of the solutions which fill the pores.
In this work we have, knowing the data the permeability and porosity of the rock and electric conductivity of the solutions under high PT, calculated the electric conductivity of the rocks and its variation as applied to the continental crust conditions.
Taking into account the complexity of the Earth's crust structure, we have restricted ourselves by the following conditions: the depth of the crust is 40 km; the temperature gradient is taken for the low and high thermal fluxes (9oC/km and 26oC/km, respectively); the crust totally consists of either granites, or gneisses, or amphibolites; the mean pressure-gradient is 270 bar/km; in the section of the continental crust Pfl = Psol , and the effective pressure is determined by the condition Peff = Psol -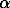 Pfl, it is constant and amounts to 30 MPa, the fluid is represented by decimolal NaCl.
Pfl, it is constant and amounts to 30 MPa, the fluid is represented by decimolal NaCl.
The method of stationary gas filtration was used to measure the permeabilities of granite, gneiss, and amphibolite at temperatures to 600oC and effective pressure 30 MPa. The effective sizes of slit-like pores were calculated [3]. The electric conductivities of rocks were calculated from the data on the initial porosity, pore sizes, and electric conductivity of the solution under the fluid pressure and the appropriate temperature.
In regions with low thermal flux the electric conductivity of amphibolite and granite actively increases by one and a half order (from 0.001 to 0.1 s) to » 5 kbar (20 km) and temperatures about 200oC (fig.1).
Fig.1.
Fig.2.
The electric conductivity of gneiss grows monotonously by a factor of 3 (from 0.03 to 0.1 s) to 2.5 kbar (» 10 km) and a temperature of 110oC and subsequently it remains constant.
In the regions with high thermal flux the electric conductivity of granite (fig.2) grows by two orders (from 0.002 to 0.2s), to » 5 kbar (15-2- km) and T» 500oC. The electric conductivity of gneiss grows by approximately one order (from 0.03 to 0.3 s ) to 25 km and T=650oC. The electric conductivity of amphibolite reaches maximum at P=2.6 kbar and T=250oC (10 km). As the depth further increases to 25 km, the electric conductivity decreases by one order (from 0.03 to 0.003s).
By comparing the change in the electric conductivity of the solutions and in the permeability as a function of the PT-conditions, we have concluded that the permeability makes the dominant contribution to the electric conductivity of rocks. At the same time none of the versions of K and c combination gives a jump-like or anomalous change of the electric conductivity of rocks.
Not denying the possibility of the two-layer structure of the continental crust we, based on our experimental data, cannot support this hypothesis. As suggested by our data the electric conductivity of fluid-saturated rocks has to increase or decrease monotonically.
The contrast alteration of the electric conductivity can result from a change in the phase state of natural fluid
37
(homogenization or heterogenization) at constant porosity and permeability of rocks.
The two-layer crust structure, from the point of view of permeability and porosity, can form as a result of instantaneous increase-decrease of the pore pressure (for example, dehydration) or certain global geophysical causes.
References:
# Shmonov V.M., Borisov M.V., Lakshtanov D.L. Investigation of permeability of rocks hosting the hydrothermal vein Pb-Zn mineralization.
key words [permeability ore mineralization]
The review of the works concerned with geochemical methods of exploration over the past 15 years has shown that no simultaneous study of aureoles of chemical-element scattering and rock permeability has been performed. It is, however, clear that permeability dictates the quantity of the ore-bearing solution which passed thorough the rock. In this work our task has been to understand the relationship between postpermeability and metal concentration in the rock.
The object of the investigation is the Pb-Zn deposits Kholst and Verkhnii Zgid from the Sadondky polymetallic ore zone. We have examined altered granites, the basic rock-forming minerals of which are quartz (25-40 wt%), plagioclase (25-40 wt%), most often oligoclase N22-26, orthoclase, microcline (20-25 wt%), muscovite and biotite (£ 7 wt%) mean-grain granites are predominant. The metasomatic processes of alteration of host granites in the neighbourhood of the veins manifest themselves as quartzization, chlorination, serpentization, and carbonatization. The basic form of the occurrence of Zn, Pb, and Cu in the veins and aureoles is sulphides.
The method of stationary gas filtration was used to determine the permeability of 40 samples of altered granites from various horizons of the deposits. The permeability of the rocks ranges from 1e-15 to 1e-18 m2 (1-0.0001 mD).
The greater spread in the permeability values is observed at a distance of first two meters away from the vein (three order). At a distance in excess two meters the permeability is constant and amounts to 1e-16m2 . The analogous scenario is observed in the behaviour of the concentration of metals in the aureole of the vein. At the first two meters the jumps of the concentration change from 9 ×
10-3 wt% to 1500 ×
10-3 wt%; at a distance in excess of 2 meters it complies with the background level of 9 ×
10-3 wt%. In this respect one can observe a qualitative agreement between the characteristics of aureoles obtained from analyses of ores and from permeability studies. The near-contact fluctuations k and 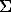 Ci are a consequence of heat treatment or a result of shock decompression upon the crack formation.
Ci are a consequence of heat treatment or a result of shock decompression upon the crack formation.
In this work [1] M.V.Borisov discusses the forms and types of scattering aureoles as a function of their space orientation, confinement to a hanging wall or a buying wall, direction of the filtration or the diffusion of the solutions towards the vein or backwards. The concentration profiles plotted vs the distance are shown in figs.1 and 2. The same figures illustrated profiles of permeability for the same sections.
Fig.1.
Fig.1 shows that at the movement from the vein into the host rocks k and 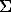 Ci , behave in a syndistant manner: an increase in the permeability is accompanied by an increase of the concentration of ore elements and, on the contrary, a decrease in the permeability is accompanied by a decrease of the ore concentration. In other words, the profile of ore concentrations repeats the permeability profile.
Ci , behave in a syndistant manner: an increase in the permeability is accompanied by an increase of the concentration of ore elements and, on the contrary, a decrease in the permeability is accompanied by a decrease of the ore concentration. In other words, the profile of ore concentrations repeats the permeability profile.
Fig.2.
Fig.2 illustrates the asyndistant k and 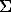 Ci , ratio: the high permeability of the sample complies with the decreased concentration of ore elements; the low permeabil-
Ci , ratio: the high permeability of the sample complies with the decreased concentration of ore elements; the low permeabil-
# The work is supported by the Russian Foundation for Basic Research grant 95-05-15354a and 96-05-64887
38
ity complies with the high concentration of ore elements. Unfortunately, the sufficient number of the samples are not available for each section, but even 2-3 samples demonstrate the same tendency.
There are two sections whose profiles cannot be confined to either direct or negative dependence. With allowance for the fact that within one sample the permeability can differ by 10 to 20 times, and the analyses regarding ore components and permeabilities were performed on concurrent samples, the correlation coefficients r=0.6-0.7 may be thought encouraging.
Permeabilities of two types are envisaged-coincident and noncoincident with the ore elements concentration profile, that is the correlation can have both positive and negative sign. So the permeability of rocks can be an additional parameter characterising scattering aureoles. The search for the general interrelation between k and 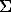 Ci in sections of the two deposits yielded the negative result. More detailed studies are required.
Ci in sections of the two deposits yielded the negative result. More detailed studies are required.
References:
Ezhov S.V. Diffusional redistribution of the substance with the formation of zoned structures in experiment.
key words [metasomatosis zoning ore deposition]
The experimental data and natural observations suggest 6 types of metasomatic zoning, when the process is due to diffusional transport of the substance.
1. Zoning due to the interaction of a rock with a solution of constant composition.
In experiment such structures form as a result of metasomatic transformation of the specimen at the open capsule end (fig.1a). One of the postulates of D.S.Korzhinskii's theory of metasomatic zoning is the ingress of solutions of constant composition which bring quite mobile components into the system (D.S.Korzhinskii, 1969). A large solution volume in the autoclave ensures conservation of its composition throughout the run (fulfilment of the postulate conditions). The zoned structures of such type were studied in detail by G.P.Zaraiskii et al (1989).
2. Contractive-bimetasomatic zoning. The runs which reproduced bimetasomatic zoning were conducted under the conditions of the solution stagnation (fig.1 a,b). In this case all the components (both 'quite mobile' and 'inert ones') behave alike - they leach out of the closest - neighbour rocks and redeposit in the contact zone. In the rock contact zone the solutions 'intermix' due to the conterdiffusion of the components as a result of which the solution becomes nonequilibrium. Calcium and silicon being predominant in the composition of the solution, the basic newly formed minerals are silicates of calcium, characteristic of skarn zones. The process is accompanied by the following effects:
- the initial difference in the concentrations of various components in pore solutions of the original rocks predetermines the irregularity of the enrichment in these components of the pore solution in the contact region which is actually the cause of the zoned distribution of the newly formed minerals;
- the precipitation of the new minerals (which implies that the components combine with each other and transit from the solution to the solid state) is accompanied by the solution sterilisation in the mineral formation zone. Precisely this sterilisation is responsible for the long upkeep of the high concentration gradient of the components in this zone compared to solutions of wall rocks and therefore the directed ingress of the components to the contact region. A gradual expansion of the escape region leads to a decrease of the gradient and decay of the process.
- the diffusion of any component at the side of wall rocks implies depletion of the pore solution in this components, i.e. the solution is no longer in equilibrium with the rock. The minerals start dissolving which contained the 'escaped' component. In the limit this dissolution may lead to complete leaching of the rock near the forming skarn column, which is often the case in experiment.
3. Zoning of ore deposition at geochemical barriers. In the runs where the specimen contained an ore material admixture the ore components diffused via granitoid pore solutions and precipitated in the contact region with limestone. Ore depositing at 300oC takes place directly at the limestone border, at 350-600oC at the borders of the simultaneously forming zones of the bimetasomatic skarn column (Ezhov, 1994). Zoning of the coskarn ore deposit of this type manifests itself in the concentration of galenite preferentially along the border with limestone, of sphalerite in the central column part, chalcopyrite and magnetite in the endocontact part. The deposition of sulphides and their zonal distribution is dictated by differences in solubility of ore minerals in pore solutions of each column zone.
4. Zoning of the distribution of scattered ore mineralization in silicate rocks. Zoning of this type is due to differences in the ore components migration rates when the precipitation of minerals occurs upon their combination with components of some minerals of the initial rocks. Diffusing sulphur combines with iron of dark granitoid minerals with the formation of scattered pyrite, a slower copper diffusion leads to a gradual replacement of pyrite by chalcopyrite (fig.1b).
5. Zoning of diffusional redistribution of the components. This one forms in ore layers at the borders of rocks different in compositions. The componental diffusion at the side of wall rocks causes the appearance of differences in the composition of pore solutions and, hence, the difference in the solubility of ore minerals at different sides of the layer. The latter predetermines the redistribution of the ore substance. In the runs the originally homogeneous mixture of sulphide minerals, placed between granodiorite-porphyry and quartz porphyry, separated to individual
39
zones of different composition over a short time period (fig.1c).
6. Zoning of ore minerals distribution in 'volumetric metasomatites'. Once the redox reaction with the participation of Fe2+ and S6+ is intensive, there can form non-zoned (volumetric) metasomatites of the skarn (or nonskarn) composition with a scattered sulphide mineralization (fig.1d). Zoning manifests itself in the space distribution of impregnations of various sulfides (pyrrhotine concentrated in the central part, cubanite at the periphery).
Fig.1. Development of the diffusion metasomatites of different types (structure schemes of samples after the runs). Temperatures within 450-460oC, P=1kb, solutions of NaCl and KCl of different concentrations.
1-6 starting components for preparing samples: 1-granodiorite (granodiorite-porphyry), 2- quartz porphyry, 3-limestone, 4-limestone with impurity of chalcopyrite elements compounds (Pb,Zn,Cu), 5- mixture of galenite, sphalerite, and chalcopyrite, 6 - FeO and FeSO4 mixture, 7-9-newly formed minerals: 7-metasomatic scarn columns of different compositions, 8- sulfides occurrence within scarn columns, 9 - scattered pyrite (a) and chalcopyrite impregnation (b) in a silicate rock, 10-zonal distribution of sulfides of initially homogeneous mixture of galenite, sphalerite and chalcopyrite, 11 - sulphide impregnation in 'volume' metasomatites. I-VI - types of zonal metasomatic transformations.
References:
#
Redkin Al.F. The estimation of f(o2) of the U3O8-UO3 × 0.33H2O assemblage using Ag-AgCl sensor procedure.key words [uranium oxide oxygen buffer hydrothermal experiment] Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, Moscow District, 142432, Russia ; Institute of the Geology of Ore Deposits, Petrography, Mineralogy and Geochemistry, Russian Academy of Sciences, 35 Staromonetny per., Moscow, 109017, Russia
U-O-H system is one of the well studied systems. The interest to uranium and its compounds relates to its using in an energy industry as a 'nontraditional fuel', though the first work on thermodynamic properties investigation dated to the beginning of the XX century [1]. Most of thermochemical investigations forming the basis of the representative handbook on thermodynamic properties of uranium oxides [2-4] refer to 1950-1980 years.
As an f element uranium can show valence from +2 to +6 in its compounds, but the states of +4, +5 [5] and +6 are most usual in natural minerals. This U property stimulates the variety of stable and unstable compounds [6]. Oxides, hydroxides and other U(VI) compounds being formed in anoxic conditions have a typical yellow or pale-yellow color, whereas black, dark-red and dark-green colors are typical for the oxides of lower degree of oxidation (from uraninite to pitchblende). This property facilitates the previous valence treatment of uranium compounds. The investigations of the geochemical condition of uraninite, nasturanium (or pitchblende) formation show that uraninite is stable in the presence of metallic Bi, Cu, magnetite, whereas for nasturanium ore deposit (O.D.) the condition close to bismut-bismutin (Bois-Noirs O.D. in France) and hematite-magnetite assemblages (uranium O.D. related with the Permian vulcanogenic-sedimentary rocks of case) are typical [7]. Native Cu is not a rarity at the nasturanium O.D. (Beaverlodge, Canada)[8]. Except that, cuprite (Cu2O) as well as tenorite (CuO) is not typical for endogenous uranium O.D. Native Bi by [9] is a satellite of uranium pitchblende. If proposed that during many billion years in deep of the Earth the equilibrium between coexisting phases with oxygen has been realized, then all the oxides of UO2+x composition, where x£ 0.92, were formed at f(O2) below the equilibrium f(O2) of Cu-Cu2O buffer. We [10] also established that hydroxides of U(VI) steadily form at f(O2) close to Cu-Cu2O in the temperature range from 300 to 500oC and water pressure of 1,000 bars. Since, these data have been in an obvious disagreement with the calculated ones, moreover Cu-Cu2O buffer used is accepted as slow working, a necessity of their confirmation by other procedures came up.
The Ag-AgCl sensor procedure [11] was undertaken to find the equilibrium f(O2) of the U3O8-UO3 × 0.33H2O assemblage. The mixture of U3O8 +UO3 × 0.33H2O with water was loaded into a big gold capsule. Two welded small thin-walled (0.01cm) platinum capsules with Ag, AgCl, 0.01mHCl (or H2O) were then placed into this Au capsule. The air of all the capsules was replaced by the
# This work was supported by grants of Russian Foundation for Basic Research 96-05-64709 and RFFI-NNIO-9605-00020 G.
40
pure argon before welding. The experiments were performed in air free (Ar media) autoclaves of 75-100 cm3 in volume. Pressure within the system was set by the measured volume of water in accordance with the known P-V-T relationship of H2O. The run duration was 14 days. The uncertainty in T and P were ± 5oC and ± 50-100 bars. The previous investigations [12] have shown that such an outfit of the run provided equilibrium O2 pressure within 3-5 days.
To describe the relationship between mHCl and f(O2), we used the experimental data of Korzhinskii [13]. At constant T and P it can be described by the linear equations log f(O2)=a+b × log mHCl with the room mean square (rms):
toC |
P, bars |
log f(O2)=a+b × log mHCl |
||
a |
b |
rms |
||
500 |
1.000 |
-23.989 |
-3.587 |
0.140 |
600 |
1.000 |
-18.668 |
-2.900 |
0.093 |
700 |
1.000 |
-16.009 |
-3.298 |
0.338 |
f(O2) values of the Ni-NiO, MnO-Mn3O4, Fe2O3-Fe3O4, Cu-Cu2O and Cu2O-CuO oxygen buffers calculated by Robie et al. [14].
The values of mHCl in 4 capsules with Ag-AgCl corresponding to U3O8-UO3 × 0.33H2O at 400oC and P=1,000 bars were measured as follows: 10-3.08, 10-2.92, 10-3.4 and 10-2.89 (average of log mHCl=-2.97). According to the table, the temperature dependence of f(O2) is of the form:
log f(O2)=20.93-26664/T (rms = 0.051, used 3 T) or
log f(O2)=15.12-22007/T (used 500 and 600oC only)
at 1,000 bar and mHCl=10-2.97. The value of log f(O2) of the U3O8-UO3.0.33H2O buffer thus estimated corresponds to -18.1± 0.6, when the Cu-Cu2O buffer gives -18.38 at 400oC and 1,000 bars.
The log mHCl values in 3 sensor capsules were -2.53, -2.51, -2.53 at 500oC and 1,000 bars, i.e. this corresponds to log f(O2) =-14.95 ± 0.4. The calculated log f(O2) value of Cu-Cu2O is found to be -15.00.
Unfortunately, there are not enough data on thermodynamic properties of UO3 ×
0.33H2O (or U3O8(OH)2) in the handbooks. Thus, we have restricted our calculations with 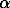 - and
- and 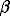 -UO2(OH)2 for which there are necessary data [4, 15]. The calculations showed that f(O2) of U3O8- UO2(OH)2 buffer occurs near fO2(Cu2O-CuO) at 25-100oC and has a tendency to grow into a more oxidative area at higher temperatures. The calculated values of f(O2) of UO2-U4O9 , U4O9-U3O8, U3O8-UO3, the other oxygen buffers and received data of the U3O8-UO3 ×
0.33H2O buffer (square symbol) are shown in the Figure. This Fig. was built on the basis of the thermodynamic data by Glushko [3]. The data of [4] as compared to those of [3] give disagreement in terms of log f(O2) from -0.53 to +0.37 at 700oC whereas at 25oC it consists only of -0.03 ¸
+0.08. The calculation shows that UO2 is stable at f(O2) corresponding to the Fe2O3-Fe3O4 buffer and is replaced by U4O9 in the vicinity of fO2(Cu-Cu2O). The U4O9 oxide should be stable at Cu-Cu2O, but U3O8 at Cu2O-CuO is stable in a wide range of temperatures and pressures. It is evident from the Fig. that the calculated data in the U-O system are in an obvious opposition with our experimental data. The analyses of So298(
-UO2(OH)2 for which there are necessary data [4, 15]. The calculations showed that f(O2) of U3O8- UO2(OH)2 buffer occurs near fO2(Cu2O-CuO) at 25-100oC and has a tendency to grow into a more oxidative area at higher temperatures. The calculated values of f(O2) of UO2-U4O9 , U4O9-U3O8, U3O8-UO3, the other oxygen buffers and received data of the U3O8-UO3 ×
0.33H2O buffer (square symbol) are shown in the Figure. This Fig. was built on the basis of the thermodynamic data by Glushko [3]. The data of [4] as compared to those of [3] give disagreement in terms of log f(O2) from -0.53 to +0.37 at 700oC whereas at 25oC it consists only of -0.03 ¸
+0.08. The calculation shows that UO2 is stable at f(O2) corresponding to the Fe2O3-Fe3O4 buffer and is replaced by U4O9 in the vicinity of fO2(Cu-Cu2O). The U4O9 oxide should be stable at Cu-Cu2O, but U3O8 at Cu2O-CuO is stable in a wide range of temperatures and pressures. It is evident from the Fig. that the calculated data in the U-O system are in an obvious opposition with our experimental data. The analyses of So298(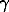 -UO3) suggest that the adopted value of 96.11 J ×
mol-1 ×
K-1 by [16, 3, 4] is somewhat small because it is far from the linear dependence of entropy on the composition in the range of U/O from 2.0 to 3.0. So298 (
-UO3) suggest that the adopted value of 96.11 J ×
mol-1 ×
K-1 by [16, 3, 4] is somewhat small because it is far from the linear dependence of entropy on the composition in the range of U/O from 2.0 to 3.0. So298 (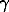 -UO3)=98.62 J ×
mol-1 ×
K-1 from [17] was used in [2]. However, such a disagreement between the experimental and calculated data (about 35-45 kJ in the reactions equalized to 1 of O2) cannot be caused by So298 only, but first of all by
-UO3)=98.62 J ×
mol-1 ×
K-1 from [17] was used in [2]. However, such a disagreement between the experimental and calculated data (about 35-45 kJ in the reactions equalized to 1 of O2) cannot be caused by So298 only, but first of all by  fHo298 .
fHo298 .
Fig. The values of f(O2) of the various oxygen buffers at total pressure of 1 kb: calculated (solid lines) and experimental (square symbols) data.
The author understands that the data presented are not enough to conclude that the thermodynamic properties of uranium oxides UO2, U4O9 , U3O8, UO3 have to be revised. The additional hydrothermal investigations are necessary to check f(O2) of the uranium oxides assemblages.
As the result of the investigations carried out, it is suggested that the equilibrium f(O2) of the U3O8-UO3 × 0.33H2O buffer assemblage approximately corresponds to f(O2) of Cu-Cu2O oxygen buffer at 400, 500oC and H2O pressure of 1,000 bars and consists of -18.1± 0.6 and -15.0 ± 0.4 in terms of log f(O2).
References:
41
Ezhov S.V. Thermodynamic modelling of the contact mineral formation.
key words [modelling skarn formation ore deposition stages]
A greatest number of the experiments concerned with a study of the contact process have been carried out under the conditions of pore solutions stagnation (without the ingress of a non-equilibrium solution capable of bringing quite mobile components into the mineral formation zone). The bimetasomatic process manifests itself in such cases as the interaction of the contacting rocks at the backgrounds of spatial redistribution of only those components which primarily occur in the initial rocks (Zaraiskii, 1989). This circumstance gives grounds for thermodynamic modeling in which case particular volumes of 'contacting' silicate and carbonate rocks, and some volume of a NaCl (or KCl) solution are included into the system, i.e., initially the solution contains no components which could be constituents of skarn minerals. The computer program of N.N.Akinfiev was used in the computations.
The studies of the following systems have yielded significant results.
1. The system granitoid-dolomite limestone. The silicate and carbonate rocks were in the volume ratio 2:1 (63.4 and 36.6%). The silicate rock incorporates quartz (16.1 vol.%), orthoclase (12.4 vol.%), plagioclase (35.1% where the fraction of albite is 1/3), and annite (35.4%). The accessory magnetite is present (1%). The second rock is represented by dolomitic limestone (25.6% dolomite). The calculation of the mineral equilibria enables one to follow the changes in the amounts of the initial minerals and the appearance of the new minerals as a function of temperature (Fig.1a). It is seen that dolomite is the first to disappear (beginning with 300oC) , as this takes place calcium goes to form additional amounts of calcite, and magnesium goes to form silicate minerals - first tremolite and at higher temperatures diopside. At 450oC quartz disappears , and there appear garnet and next wollastonite. The amount of ferric iron of the accessory magnetite limits the development of epidote.
The system granitoid-anhydrite-dolomitic limestone. The system differs from the previous one in the occurrence of anhydrite in the carbonate rock composition (17.6 vol%, with 24.7% dolomite and 57.6% calcite). The drastic change in the mineral formation behaviour as compared with system 1 is due to the redox reaction with the participation of sulphur and iron. The overall sulphur of the anhydrite reduces to enter the composition of the newly formed pyrite, the ferrous iron of biotite oxidises stipulating the occurrence of large amounts of epidote, hematite, and magnetite. The process goes throughout the temperature range investigated (300-600oC ) at the background of the 'normal' transformation of mineral skarn associations as a function of temperature (Fig.1b). The method enables one to study the transformation of the mineral associations not only in the 'progressive' (with increasing temperature) but, also, in the 'regressive' with decreasing temperature directions.
The decomposition of the skarn minerals under the regressive conditions is accompanied by a successive replacement of high-temperature associations by lower-temperature ones. The characteristic herewith is the appearance of quartz and calcilte. The obtained materials suggest that
1. Thermodynamic modeling using the model of 'sterile' solution (with respect to quite mobile components) describes adequately the skarn formation process, in particular, the successive replacement of mineral associations at progressive or regressive temperature variation.
2. Precipitation of ore minerals, with the inclusion of sulfides may combine with the skarn formation throughout the temperature range. The ore formation may be genetically related to the skarn formation via redox reactions with the participation of Fe and S.
Temperature decrease is accompanied by decomposition of skarn minerals to yield quartz, calcite, epidote,
42
actinolite which is usually treated as the manifestation of the acidic stage of the process. Whence one may conjecture that the acidic stage of mineral formation in skarns may have the autoreactive nature evolving without the ingress of new portions of hydrothermal solutions. Simultaneously with the regressive transformation of skarns the ore mineralization contained in them also transforms.
Zavarzina D.G. , Migdisov Art.A. , Alekhin A.V. Investigation of biogeochemical dissolution of fine dispersed sulfur in low temperature hydrothermal systems.
key words [sulfur microorganism desulfurella kamchatkiensis]
Lomonosov Moscow State University Geol. Dep.
In the recent decade microbiologist have described a large number of sulfur-reducing microorganisms which use the reduction of elementary sulfur to hydrogen sulfide as the principal energy supplying reaction. Among these is the recently discovered thermophile acetate-using sulfur reducer Desulfurella kamchtkiensis. As sulfur is one of the important components of thermal solutions and its regime largely determines the occurrence of the hydrothermal process, it was important to determine the role of bacteria of the new group in the geochemical sulfur circulation.
The goal of this work was to understand the influence of sulfur-reducing bacteria on the fine dispersed sulfur dissolution rate in low-temperature hydrothermal solutions. The problems to be elucidated in experiment were:
1) What does D. kamchtkiensis use as an electron acceptor: is it elementary sulfur or polysulfures?
43
2) What is the effect of D kamchtkiensis. on the dissolution rate of fine dispersed sulfur?
The concentration of hydrogen sulfide and dissolved sulfur in a solution was determined by the potentiometry method, making it possible to carry out the required measurements in the process of anaerobic culture growth. To solve the first part of experiment we performed a series of runs where different initial pressures of hydrogen sulfide and therefore different initial concentrations of polysulfanes in equilibrium with it were given.
The obtained curves of the yield of hydrogen sulfide being a D. kamchtkiensis metabolism product, have shown that the most favourable growth conditions were those under which the given initial concentrations of polysulfares and hydrogen sulfide were maximal.
This fact correlates with the curves of growth of D. kamchtkiensis and acetate consumption. The results of the run are consistent with the suggestion that D. kamchtkiensis uses as an electron acceptor polysulfanes rather than sulfur.
To solve the second problem we performed two runs, viz. with sulfur reducer and without it. In the first case a solution containing fine dispersed sulfur was introduced into the three-day D. kamchtkiensis culture. pH, of hydrogen sulfide with an Ag/Ag2S-electrode was measured, that of the dissolved sulfur with a platinum Eh-electrode. In the abiogenic run the starting conditions were analogous, but the run was conducted in the absence of the bacteria.
In the biogenic run in the first minutes after the introduction of fine dispersed sulfur the concentration of the dissolved sulfur decreased as a result of the polysulfanes formation. Several minutes after the formation of polysulfanes they began to decompose, and the concentration of the dissolved sulfur increased. During that event some part of polysulfanes was used by D. kamchtkiensis in the energy reaction. 2 hours after the beginning of the run the concentration of the dissolved sulfur started decreasing again which we interpret as a consequence of decreasing dispersity of sulfur due to dissolution of the fine dispersed fraction as most reactable. In 3 hours the concentration of sulfur stabilized.
In the abiogenic run after the introduction of fine dispersed sulfur the decrease of the concentration of the dissolved sulfur due to the formation of polysulfanes also occurred but as contrasted from the biogenic run the process took 2 hours and then there began a slow decomposition of polysulfanes accompanied by an increase of the dissolved sulfur concentration. This decomposition went on till the end of the observation.
The studies performed suggest that:
1. D. kamchtkiensis uses polysulfanes, being a well-soluble equilibrium form in the system So-H2S, as the electron acceptor.
2. The growth of D. kamchtkiensis favours the dissolution of fine dispersed sulfur shifting the chemical equilibrium towards the formation of polysulfanes according to the equation So + H2S =H2S2.
Yakovleva V.P., Migdisov Art.A. , and Alekhin Yu.V. Experimental study of molecular complex formation in the Sb2S3-H2S system by the solubility method.
key words [antimony hydrogen sulphide gas]
Modern studies of low-temperature volcanic emanations show that the significant transport of the ore substance can occur under these conditions. Hydrothermal systems are rather characteristic of the presence of hydrogen sulfide in the gas phase. It seems reasonable to assume that such an active complex-forming agent as hydrogen sulfide is capable of forming sulfide molecular complexes with metals not only in aqueous solutions, but also in the gas phase. Unfortunately, information about the solubility of sulfides in gaseous hydrogen sulfide is presently almost completely scarce. Therefore, we studied the solubility of antimonite in hydrogen sulfide, because this mineral is rather characteristic of low-temperature hydrothermal systems.
Experiments were carried out at 290oC in thin-walled lightened autoclaves by the method of separated phases. The pressure was specified by the amount of hydrogen sulfide, which was introduced by freezing on, and calculated from the PVT data. In the gas solution formed above antimonite in the one-component system, Sb2S3(g), SbS(g), and S8(g) species predominate, which are formed in the reaction:
Sb2S3(s) = Sb2S3(g) (1)
Sb2S3(s) = 2SbS(g) + 1/8S8(g) (2)
To separate effects related to the transport of antimony in the form of Sb2S3(g) and SbS(g), we carried out experiments in the Sb2S3-H2S-S and Sb2S3-H2S systems. In the first case, according to reaction (2), the formation of the SbS(g) species is suppressed, and the transfer of antimonite is determined by the form of Sb2S3 and its derivatives.
The experimental values of the solubility of antimonite in hydrogen sulfide in the Sb2S3-H2S-S system are presented in Fig. 1 (black points). It is remarkable that the amount of the dissolved Sb2S3 is proportional to the molar amount of the introduced hydrogen sulfide in the whole range of the parameters studied. A high degree of the solvation processes is evident, because if hydrogen sulfide behaves as an inert solvent, the amount of the transferred antimonite would be constant and reflected in Fig. 1 as a line parallel to the X axis.
This process in the general form can be described by the gas-phase stoichiometric reaction:
Sb2S3 + mH2S = Sb2S3 × (H2S)m (3),
where m is the solvate number.
The differentiation of the thermodynamic constant of this reaction with respect to pressure gives the ratio
(dlnX/dlnP)T = m - 1 - dlnZ/dlnP (4),
where X is the molar fraction of the transferred antimonite, P is the pressure in the experiment, and Z is the generalized coefficient of the nonideal character of the system, which takes into account both the nonideal character of the components and gas of mixing.
44
The dependence of the amount of the transferred antimonite on the amount of the introduced hydrogen sulfide is linear (Fig. 1). A conclusion that the molar fraction of the antimony complexes in the gaseous solutions of hydrogen sulfide is constant automatically follows from the linearity in the coordinates mol Sb2S3 - mol H2S. Thus, based on expression (4), the linearity of the dependence of lnX on lnP ((dlnX/dlnP)T = const) results in a conclusion that the effects related to the nonideal behavior of the gas mixture cannot be taken into account, and the slope angle ((dlnX/dlnP)T = 0) suggests the value of the solvate number as m = 1.
The data obtained for the Sb2S3-H2S system are presented in Fig. 1 (white points). Two main processes of the dissolvation of antimonite occur in the system: the solvation of Sb2S3(g) and the formation of the SbS(g) species and hydrogen polysulfide H2S2(g):
Sb2S3(s) + H2S(g) = Sb2S3 × H2S(g) (5)
Sb2S3(s) = 2SbS(g) + 1/8S8(g) (6)
H2S(g) + 1/8S8(g) = H2S2(g) (7)
The formation of hydrogen polysulfides in reaction (7) results in the shift of equilibrium (6). Based on the calculation from Veselovskii's data, our system can be well described by these reactions, and the calculated amount of SbS(g) coincides with the value obtained from our experimental data. Thus, the solubility in the Sb2S3-H2S system is described by the formation of two species SbS(g) and Sb2S3 × H2S(g) and is equal to 5.4 × 10-6.
Fig.1.
Yagova O.E. 1, Rusakov V.S. 1, Kuz'mina N.A.2, Bychkov A.M. 2 Mössbauer studies of the kinetics of the low-temperature synthesis of acmite under hydrothermal conditions.
key words [acmite hydrothermaql synthesis]
Lomonosov Moscow State University Phys. Dep.; Vernadsky Institute of Geochemistry and analytical Chemistry RAS Moscow
Investigations of the mechanisms and kinetics of the mineral formation processes are most important for experimental geochemistry. In particular, the mechanism of transformation of the original X-ray amorphous iron-bearing material to chain silicates appears to be interesting. Acmite NaFeSi2O6 - a mineral of the pyroxene group - is a suitable subject to study the crystallization processes of chain silicates as it readily crystallizes under the laboratory conditions from mixtures of the appropriate oxides and salts, glasses and gels, and is reliably identified by present-day physical methods. In nature the formation temperature of acmite ranges broadly from the values characteristic of crystallization of alkali magmas to much lower values characteristic of alkaline metasomatosis and diagenesis.
In this work the kinetics of acmite synthesis from gel under low temperature hydrothermal conditions was studied by Mössbauer spectroscopy methods. The initial material was dry gel of the composition Na2O × Fe2O3 × 8SiO2 . The synthesis was carried out at a temperature of 275oC and a pressure of saturated vapours. The synthesis time-period varied from 1h to 47days.
The M'ssbauer spectra of the samples were doublets of the paramagnetic type. In the shortest runs and in the ones longer than » 12d these are symmetric doublets with the values of isomeric shift and quadrupole shift characteristic of small particles of Fe2O3 and acmite, respectively. For the runs of 3 hour to several days long superposition of two partial spectra of gel and acmite was observed.
The figure illustrates the dependence of the relative intensity I of the partial spectrum of acmite on the synthesis time period ts . The crystallization of acmite begins 2.5h after the onset of the synthesis process and proceeds with the characteristic time of decrystallization of gel t =6.7h. The analysis of the values and the character of alteration of the hyperfine interaction parameters with the synthesis time (see the figure) suggests the following conclusions. The process of the low-temperature synthesis of acmite proceeds in several steps: first there forms the 'precursor phase', next acmite crystallizes from the 'precursor phase' and then crystals grow via the surface layer recrystallization. Only fine-disperse superparamagnetic particles of Fe2O3 measuring not greater than about 80 Å are present in the initial gel and the synthesis products.
45
At all steps of the formation of acmite in the process of crystallization the finest Fe2O3 particles participate first of all. The observed correlated dependencies of the isomeric shifts 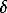 and quadrupole shifts
and quadrupole shifts  of the partial spectral components of gel and acmite of the synthesis time are associated with the increase of the mean particle size of the synthesis products. The obtained values of the widths of the partial Mössbauer spectra components lend support to the validity of the drawn conclusions.
of the partial spectral components of gel and acmite of the synthesis time are associated with the increase of the mean particle size of the synthesis products. The obtained values of the widths of the partial Mössbauer spectra components lend support to the validity of the drawn conclusions.
Kotelnikov A.R. , Orlova A.I. , Pet'kov V.I. , and Koval'skii A.M. Experimental study of solid (Na,K)Zr2(PO4)3 solutions by the method of ion-exchange equilibria with fluid at 450oC and P = 1 kbar .
key words [zirconium-phosphate fluid ion-exchange]
Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, Moscow Region, Russia; Nizhnii Novgorod State University, Nizhnii Novgorod, Russia; Moscow State University, Moscow, Russia
Ceramic materials based on zirconium-phosphates (general formula MeI, MeII (MeII,Zr)2(PO4)3, where MeI = Na, K, Rb, Cs, Mg, Ca, Sr, Ba; MeII = La...Lu, U, Pu...Am) are promising matrices for immobilization of radionuclides due to (1) wide limits of isomorphic substitutions; (2) high stability to leaching processes; and (3) stability toward radiation damage [1, 2]. To forecast the behavior of the NZP matrices in the Earth crust, one should know their thermodynamic properties and mechanism of cation-exchange reactions with the fluid. For this purpose, we carried out ion-exchange experiments in the NZP-fluid system under hydrothermal conditions.
Experiments were performed by the ampule method in high-pressure apparatuses with a cool seal and external heating. The accuracies of temperature and pressure regulation were +5oC and +50 bar, respectively. The duration of experiments was 30 to 40 days. The approach to the equilibrium isotherm was performed from two sides. The phase and chemical compositions of solid products were analyzed by the X-ray and microprobe methods, and solutions were examined by the AAS method. According to the results of the X-ray study, alkali zirconium-phosphates were the only phase in the solid products.
The sodium, potassium, and cesium distribution was studied in the fluid-(Na,K)Zr2(PO4)3-NZP phase system; experiments were carried out at 400-450oC and 1 kbar in 1M solutions of (NaCl + KCl) and (NaCl + CsCl).
We studied ion-exchange reactions of the following type:
NaZr2(PO4)3 + KCl(fl) = KZr2(PO4)3 + NaCl(fl) (1)
1. (Na,K)Zr2(PO4)3-fluid system. The results of studying the ion-exchange reaction are presented in Table 1 and Fig.1. It is seen that the potassium and sodium distribution between the NZP phase and fluid is not perfect. Potassium enriches the NZP phase as compared to the fluid in the whole range of compositions. The NZP composition in products of one experiment vary within 1-4 mol.%, which suggests that the ion-exchange reaction is complete and the equilibrium in the system is easily reached.
The dependence of the distribution coefficient (KD) on the solid solution composition was calculated from the experimental results:
lnKD = 0.0331 + 3.7·(XK)NZP (2)
Based on this dependence, we calculated the values of the Margulus model parameters: W1 = W2 = 1.109(30) kJ/mol.
2. (Na,Cs)Zr2(PO4)3-fluid system. The results of studying the ion-exchange reaction are presented in Table 2. Unlike the (Na,K)NZP-fluid system, the equilibrium was not reached in this system. Despite the considerable change in the compositions of both the NZP phase and fluid, the compositions of the products vary substantially (up to 100 mol.%). It can be assumed that in these experiments the recrystallization of the NZP phases occurs rather than the ion exchange. This can be related to a considerable deviation of this system of solid solutions from ideal one (due to a great difference between the radii of the isomorphic sodium and cesium cations and those of sodium and potassium).
As mentioned above, the NZP phases are potential matrices for immobilization of radionuclides. Therefore,
46
the study of exchange reactions in the NZP-fluid systems gives an information about their behavior upon prolonged existence in the Earth crust rocks, because heating of the matrix due to the decomposition of radionuclides activates hydrothermal processes in the matrix-solution-host rock system. The results of studying the reactions in the NZP-fluid systems showed that a heavier element enriches zirconium-phosphates relative to the coexisting solution. In the (Na,Cs)NZP-fluid system, reactions are difficult, they occur via recrystallization of zirconium-phosphates, and Cs remains predominantly in the solid phase. Based on the experimental data obtained, we conclude that the NZP ceramics can be efficiently used for immobilization of cesium radionuclides.
Table 1. Conditions and results of experiments on studying cation-exchange reactions in the zirconium-phosphate-fluid system at 450oC and P = 1 kbar1)
|
Entry no |
Weighed sample; mg of the NZP mixture |
Solution, mcl |
XKNZP |
Ex3) |
XKfl |
lnKD |
|
|
NaCl |
KCl |
||||||
|
4654 |
60 |
220 |
- |
0.23 |
0.01 |
0.110 |
0.882 |
|
4655 |
56 |
164 |
41 |
0.52 |
0.03 |
0.125 |
1.981 |
|
4657 |
60 |
154 |
66 |
0.69 |
0.04 |
0.146 |
2.535 |
|
4658 |
63 |
115 |
115 |
0.86 |
0.01 |
0.210 |
3.140 |
|
4659 |
48 |
70 |
105 |
0.93 |
0.04 |
0.231 |
3.795 |
|
4660 |
58 |
43 |
172 |
0.96 |
0.03 |
0.420 |
3.501 |
|
4661 |
44 |
- |
160 |
0.98 |
0.02 |
0.590 |
3.528 |
Note: 1) Duration of experiments was 39 days. 2) 1 molar solutions of (NaCl + KCl) were used. 3) Ex is the error of determination of the composition. 4) The NZP mixture is a mixture of NaZr2(PO4)3 and KZr2(PO4)3 in the 1 : 1 (wt/wt) ratio.
Table 2. Conditions and results of experiments on studying cation-exchange reactions in the zirconium-phosphate - fluid system at 400oC and P = 1 kbar1)
|
Entry no |
Weighed sample |
Solution, mcl |
XCsNZP |
Ex |
XCsfl |
lnKD |
|
|
NaCl |
CsCl |
||||||
|
4190 |
60 |
- |
335 |
0.231 |
0.14 |
0.77 |
-2.42 |
|
4191 |
60 |
84 |
250 |
0.0 |
- |
0.52 |
- |
|
4193 |
60 |
210 |
70 |
0.341 |
0.38 |
0.18 |
0.85 |
|
4195 |
60 |
240 |
80 |
0.380 |
0.08 |
0.35 |
0.13 |
|
4196 |
60 |
160 |
160 |
0.620 |
0.12 |
0.50 |
0.49 |
|
4197 |
60 |
80 |
240 |
0.735 |
0.17 |
0.65 |
0.40 |
Note:1) Duration of experiments was 30 days. 2) 1 molar solutions of (NaCl+CsCl) were used. 3) NaZP is NaZr2(PO4)3; CsZP is CsZr2(PO4)3.
References:
Kotelnikova Z.A. , Chepkaya N.A. , and Ivanov D.Yu. Simulation of trapping and post-trapped changes in fluid inclusions.
key words [fluid inclusion experiment]
Institute of Lithosphere, Russian Academy of Sciences, Moscow, Russia
The following assumptions are usually used for studying fluid inclusions (FI):
1. Fluid inclusions reflect adequately properties of mother media.
2. For superimposed processes, inclusions retain the initial densities and compositions.
We experimentally studied substantiation of these statements.
According to their genesis, FI are divided into two main classes: primary (syngenetic to the crystal-host) and secondary (appeared on welding of fractures). Mechanisms of their formation differ. Trapping of the primary FI was simulated during the hydrothermal crystal growth on seeding, and the secondary FI were modeled during fracture welding.
Synthetic secondary FI were obtained in quartz, calcite, fluorite, and sanidine. All of them corresponded in density and composition to the conditions of syntheses. However, the primary FI, which can trap fluids from the boundary near-crystal layer not corresponding to the total solutions, are usually most doubtful. The synchronic syn-
47
thesis of the primary and secondary FI carried out in solutions with different compositions and densities showed that the primary FI corresponded to experimental conditions. Under homogeneous conditions, the compositions and densities of primary and secondary inclusions coincide (taking into account the experimental accuracy). Therefore, it can be concluded that the effect of the processes in the boundary layer during FI trapping cannot be determined by standard thermobaric geochemical measurements.
Under heterogeneous conditions, scatter of homogenization temperatures and compositions is very high, which confirms heterogeneous trapping. Crystals did not grow above the interface. No low-dense inclusions were observed below the interface.
The study of the total compositions of the inclusions by gas chromatography and analysis of water extracts showed that some (within an order of magnitude) correspondence between the initial compositions and results of the analysis was observed for FI trapped under homogeneous conditions, while for FI of heterogeneous trapping, the data obtained can be considered only as the qualitative composition. We explain this fact by different welding abilities of the immiscible phases, owing to which the number of inclusions containing concentrated and denser solutions is disproportionately greater than that of low-dense inclusions.
A large complex of experimental studies was carried out for post-trapping changes in the inclusions. The minerals with the preliminarily studied FI were subjected to the metamorphosing action of fluids with different chemical and phase compositions for 14-86 days, after which the inclusions were studied once more. The experimental parameters were chosen in such a way that the temperature and pressure were either higher or lower than those of the growth of the crystal-host.
The following changes in FI were observed after the experiments. 1. Shape: FI became more isometric, with more developed faced shapes, tending to gain the shape of the negative crystal. 2. Density: depending on (a) experimental conditions, (b) growth parameters, and (c) properties of the crystal-host, the homogenization temperature could remain unchanged, the inclusion could extend or open (the difference between new and initial temperatures ranged from 2 to 80oC). 3. Composition: changes were observed in some inclusions (in both water-carbonate and water-salt), and the majority of compositions remained unchanged. Some FI changed both their density and composition.
A great attention was paid to the dislocation structure of the mineral-matrix and its relation to inclusions. It is shown that the density of dislocations around inclusions increases. For superimposed processes, the character of the dislocation structures changes: dislocation channels buckle, dislocation loops and rosettes appear. The dislocation environment around FI can be easily transformed and serves for matching of the lattice defects. Therefore, (when the strength does not exceed the yield limit), the higher the dislocation density, the more stable the inclusion. Heating results in the appearance of the microcleavage aureole around the inclusions, which increases the inclusion volume. When heating is continued and the internal pressure increases, the microcleavage structure is used as the leakage channel. When the dislocation channels get out of the crystal surface, they can be used for the mass exchange, which changes both the density and the composition of FI. We attempted to estimate quantitatively a relation between changes in the external parameters and inclusion sizes. For two groups of inclusions different in volume by an order of magnitude, new homogenization temperatures were measured after overheating by 100-150oC under hydrothermal conditions at different external pressures. Extrapolation of the obtained dependences to the moment of opening of the inclusions when  Thom = 0 gave the equation of the dependence of changing of new homogenization temperatures on the external pressure and sizes of the inclusion.
Thom = 0 gave the equation of the dependence of changing of new homogenization temperatures on the external pressure and sizes of the inclusion.
#
Plechov P.Yu. * * and Kotelnikov A.R. ** ** Synthesis of artificial melt inclusions in the KAlSi3O8 - NaAlSi3O8 system.key words [artificial melt inclusions]
*Chair of Petrology, Moscow State University, Moscow, Russia **Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, Moscow Region, Russia
The majority of real mechanisms of trapping melt inclusions by a mineral-host is considered in classic works by Roedder [1] and Lowerstern [2]. In this work, we consider possible mechanisms of trapping inclusions for experimental and natural objects and compared the synthesized melt inclusions with the natural ones. This study is required for estimation of errors of procedures for studying natural melt inclusions and understanding processes resulting in distortion of the composition of the mineral-forming medium in natural melt inclusions.
We carried out a series of experiments on the synthesis of melt inclusions in alkaline feldspars. Mixtures of albite (Ab) and potassium feldspar (Or) with different microadditives (TiO2, Ni2O3, Mn2O3, and Cr2O3) were used as the starting materials. The charge was heated to 900oC (approximately by 40-50oC higher than the liquidus temperature) and exposed under these conditions for 3 h (for complete melting and homogenization of the melt). Then the temperature was reduced to subliquidus, and the system was exposed for 3 days. Since microadditives in this system played a role of modifiers, the authors managed to follow different stages of the formation of crystals and melt inclusions in these crystals.
Trapping of melt inclusions in the central zone of the growing crystal. As seen in Fig.1, the beginning of the crystal growth of alkaline feldspar (Fsp) is characterized by a great amount of heterooriented crystallites surrounded by more general contours corresponding to the crystallographic contours of Fsp.
# The work was supported by the Russian Foundation for Basic Research, Project no. 96-05-64911
48

Fig.1. The initial stage of Fsp crystal growth from melt.
Conditions: Mix composition: (65wt% Ab+35 wt%Ort)+TiO2 +Ni2O3 +Mn2O3 +Cr2O3)-0.5 mg of each. Total weight of mix 150 mg. Fluid :25 mg of H2O; Run: 760oC. P=5.3 kbar, duration 3 hour, then T decrease to 720oC (P=5.1 kbar), then 2 days of waiting.
Fig.2. Melt inslusions trapping in the crystal core.
Conditions: Mix composition (65wt% Ab+35 wt%Ort). Total weight of mix 150 mg. Fluid: 25 mg H2O. Run: 760oC. P=5.3 kbar, 3 hour of duration, then T decrease to 720oC (P=5.1 kbar), 2 days of duration
|
N |
Si |
Al |
Na |
K |
|
KG2 |
68.74 |
19.51 |
6.29 |
4.83 |
|
KPL2 |
65.47 |
19.24 |
3.18 |
11.85 |
|
KPL3 |
65.14 |
18.78 |
2.98 |
12.55 |
|
KPL3 |
64.78 |
18.75 |
2.97 |
12.4 |
|
KPL4 |
65.09 |
18.56 |
2.71 |
12.99
|
Fig.3. Natural melt inclusions in the core of the plagioclase from Apakhonchich lava flow, Klyuchevskoy volcano, Kamchatka
49
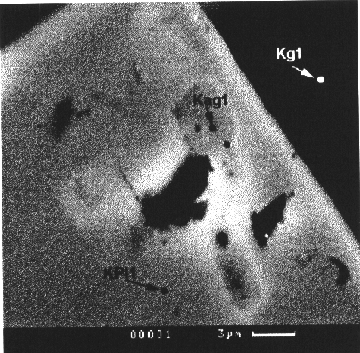
Fig.4. Areas with different electronic density and equal composition in the Fsp.
Conditions: Mix composition (65wt% Ab+35 wt%Ort). Total weight of mix 150 mg. Fluid: 25 mg H2O. Run: 760oC. P=5.3 kbar, 3 hour of waiting, then T decrease to 720oC (P=5.1 kbar), 2 days of waiting
|
N |
Si |
Al |
Na |
K |
|
KG5 |
69.41 |
19.54 |
6.63 |
4.29 |
|
KPL5 |
65.34 |
19.18 |
3.95 |
11.17 |
|
KPL6 |
64.98 |
19.26 |
3.14 |
11.85 |
Fig.5. Origin of the melt inclusions by crystallization of the internal areas of Fsp.
Conditions: Mix composition (65wt% Ab+35 wt%Ort). Total weight of mix 150 mg. Fluid: 25 mg H2O. Run: 760oC. P=5.3 kbar, 3 hour of waiting, then T decrease to 720oC (P=5.1 kbar), 2 days of waiting
|
N |
Si |
Al |
Na |
K |
|
Kag1 |
65.45 |
18.81 |
3.01 |
12.42 |
|
KG1 |
68.39 |
19.52 |
6.74 |
5.04 |
|
KPL1 |
65.23 |
19.16 |
3.30 |
12.16 |
Fig.6. Natural plagioclase from basalts (Apakhonchich lava flow, Klyuchevskoy volcano) with melt inclusions, which are distributed to zones of growth.
50
These crystallites were intergrown during the subsequent growth to form a core of the growing crystal. Since the crystallites were primarily oriented in different directions, this intergrowing is not always complete. This results in the formation of a "porous" central zone of the crystal saturated by melted inclusions (Fig.2). These "porous" central zones of crystals are rather abundant in natural crystals. For example, the plagioclase (Pl) grain from highly aluminous basalts of the Apakhonchich flow (Klyuchevskii volcano, Kamchatka), in which the central zone is saturated by partially crystallized melted inclusions, is presented in Fig. 3.
This mechanism of formation of melted inclusions assumes that the already existing crystals of the growing mineral are absent in the melt and corresponds to the beginning of crystallization of the given mineral in the magmatic system. This conclusion offers an additional criterion for interpretation of natural melt inclusions. Inclusions with similar morphology correspond to the earliest melt for the mineral under study and make it possible to determine reliably the physicochemical parameters of the beginning of crystallization of a given mineral phase.
The statement described above can be confirmed by the fact that the melted inclusions in the plagioclase grain in Fig. 3 (highly aluminous basalts of the Alakhonchich flow, Klyuchevskii volcano, Kamchatka) are most magnesial and least siliceous of more than 300 inclusions studied in 150 plagioclase grains from this flow.
Trapping of melted inclusions by growing crystal faces. In the study of the experimental material obtained, we described another mechanism of formation of melted inclusions. Fig. 4 presents the photograph of the Fsp grain obtained in secondary electrons on a Camscan-4DV electron microscope. It is well seen that different zones of the growing crystal possess different electron densities. The electron density depends on the physical density of a substance and on the average atomic number of the phase under analysis. As can be seen from the analyses presented in Table 1, different zones of this crystals do not differ in chemical composition. Thus, brightness of different zones of the crystal in the photograph (Fig.4) is related only to the phase density or, in the other words, to the degree of crystallinity of a substance in these zones, since the crystalline phase is always denser than the glass with the same composition. It can be seen in the photograph that this crystal grows by separate surfaces between which a space filled with a less dense substance with the same composition (Table 1) as the growing Fsp crystal remains.
During the further growth, the "glassy" zone of the crystal decreases in volume, growing additionally the Fsp structure. Since the initial density of this trapped zone was less than the Fsp density (shown above), cavities should be formed during the crystallization of this zone. The glassy inclusions formed in these zones are shown in photograph 5. The composition of these inclusions reflects the residual melt obtained upon overgrowing of the internal zone of the crystal rather than the composition of the mineral-forming melt. The inclusions formed by this method can be most likely attributed to zones of the crystal growth, uniformly distributed over these growth zones, and have comparatively small sizes.
Zones of the mineral-host growth saturated by a great number of fine melted inclusions (Fig.6) are often observed in natural crystals. The existence of the mechanism of formation of inclusions by overgrowing of the trapped noncrystalline zone does not imply that all inclusions with similar morphology do not correspond to the composition of the mineral-forming medium. However, to avoid errors of determination of the melt composition, one should study melted inclusions differing in morphological features and correlate each type of the inclusions to possible mechanisms of their formation.
Thus, under experimental conditions, we showed several specific mechanisms of formation of melt inclusions. The analysis of these mechanisms and comparison with natural objects gives an additional information on conditions of trapping natural melted inclusions, allows one to interpret correctly the results obtained and avoid errors related to distortion of phase ratios and compositions of the melt upon trapping of melt inclusions by natural crystals.
References:
51