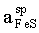
Mineral equilibria in silicate and ore systems
Fed'kin M.V., Osadchii E.G., and Kotova A.A. Measurements of FeS activities in the Zn-Fe-S-(O) system.
key words [sphalerite activity galvanic cell]
The FeS activity in the sphalerite solid solution Zn0.8Fe0.2S (sphalerite) was measured relative pyrrhotite (po) with the help of the high-temperature solid-state galvanic cell:
Pt, FeS(in sp), FeS2, Ag2S |AgI| FeS(po), FeS2,Ag2S, Pt (A)
AgI was used as a solid electrolyte with Ag+-conductivity. The measurements were performed at 750 K.
The following reactions proceed in the left and right half-cells of cell (A) respectively:
FeS(in sp) + Ag2S = FeS2 + 2Ag (I); (I);
K(I) = aAg2(I)/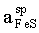
FeS(po) + Ag2S = FeS2 + 2Ag (II);
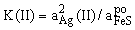(2)
Since equilibria (I) and (II) are independent of the gaseous phase, a galvanic cell with common gas space could be used. The electromotive force (EMF) of cell (A) only results from the difference in FeS activity between equilibria (I) and (II). The relationship between the EMF and FeS activities in the above reactions can be written as follows:
ln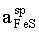
- ln
= 
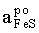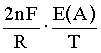(3)
where E(A) is EMF of cell (A), and n is the number of electrons transferred in the electrochemical process [n=1 in case of cell (A)]. This equation is the result of combination of mass-law equations for reactions (I) and (II) and the Nernst equation for cell (A).
Previously, the FeS activities in sphalerite solid solutions of four different compositions (10, 20, 30, and 40 mol % FeS) were experimentally measured in the temperature range 850-1020 K with a double-tube cell with separate gas space (Osadchii and Lunin, 1994):
Pt,FeS(in sp),Fe3O4,Ag,Ag2S |YSZ| FeS(po),Fe3O4,Ag,Ag2S,Pt (B)
where YSZ is Y2O3-stabilized ZrO2 (O2--conducting solid electrolyte). Pyrrhotite was used as a standard phase, and sulfur fugacity in both sample and reference systems was buffered by the Ag/Ag2S assemblage.
The application of cell (A) presented in this study expands the temperature range of the experimental data and enables the determination of the FeS activities at relatively low temperatures. It is also of great interest to compare the FeS activities in sphalerites participating in different solid-phase equilibria.
Equilibria with sphalerite are very sluggish at low temperatures. Thus, only one experimental data point was obtained as a result of a half-year run [E(A) = 17.94, T = 752 K], which corresponds to 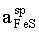= 0.902. This activity value was derived from equation (3). The FeS activity in pyrrhotite in equilibrium with pyrite (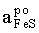=0.52) was estimated from Toulmin and Barton's data (1964).
The activity value obtained in cell (A) fits well to the extrapolated curve of FeS activities in sphalerite with 20 mol % FeS obtained in cell (B) at higher temperatures (see figure). This result confirms the satisfactory applicability of cells with common gas space based on the AgI-electrolyte to activity measurements in solid solutions and offers prospects for high-pressure experiments.
In this context, the experimental calibration of the sphalerite cosmobarometer (sp+tr+Fe) seems very promising. In estimation of pressure values by the sphalerite cosmobarometer, the equilibrium temperature of formation of the sp+tr+Fe assemblage is assumed to range within 500-550oC. According to many published data, below 500oC, diffusion becomes negligible, and no changes in sphalerite composition occur on further cooling. Cell (A) makes it possible to determine the FeS activity - pressure relationship in the sphalerite solid solution just in this temperature range.
References:
# This work was supported by the RFBR (Project N. 96-05-64311 and N. 98-05-64104)
41
#Alekseev V.A., Medvedeva L.S., Tatsii Yu.G., Bannykh L.N. Substitution mechanisms of albite to sanidine. 1. Compensation mechanism.
key words [albite sanidine substitution kinetics mechanism]Vernadsky Institute of Geochemistry and analytical Chemistry, RAS.
The runs concerned with the substitution reaction of albite to sanidine (Ab San) in a 0.1 m KHCO3 solution at 300oC, 88 bar and pH 9 involved 3 fractions of mixtures of ground minerals with different mean grain size (d) : 4.5, 16, and 73mm . The surface areas (m2) of albite (Sab) and sanidine (SSn) varied for each fraction. The runs were conducted in sealed platinum capsules in the presence of quartz that ensured a high concentration of silica (0.02m) in the solution, suppressing side reactions. The rate of the reaction in question ( r) (mol/kg/s) was measured from the slope of the kinetic curves in the coordinates Na concentration - time. The results of the runs are given in fig. 1. The straight line approximating these data fits the equation
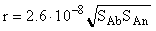(1)
In order to check how much this dependence agrees with the mechanism involving the equations of dissolution rate of primary albite (rAb) and precipitation rate of secondary sanidine (rSan) we have solved the following system of differential equations wherein variations in time (t) of molal concentration of Na, K, Al and Si in the solution are expressed via the rates and stoichiometry of the both reactions
dmNa /dt = rAb/M, (2)
dmK / dt = -rSan/M, (3)
dmAl / dt = (rAb- rSan)/M, (4)
dmSi / dt = 3 (rAb - rSan)/M, (5)
where M is the mass of water in the solution. The equation of the primary albite congruent dissolution rate has the form
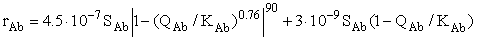(6)
Here Qab and Kab are the activity quotient and the equilibrium constant of the reaction (Kab = 3.4.10-13). This equation is a modified version of the equation derived by us earlier [1]. We have added the second term to correlate the results of the kinetic and equilibrium runs. Two terms correspond to two types of surface sites with a drastically different activity (regular and defect ones) The equation of the precipitation rate of sanidine has the form:
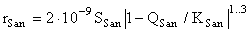(7)
where Qsan and Ksan are the activity quotient and the equilibrium constant of the sanidine congruent dissolution reaction (Ksan=7.9.10-14 [1]). The surface area of sanidine Ssan in this equation is represented by the sum of surface areas of seed crystals Ss and sanidine crystals nucleated on the albite surface [2].
Ssan= Ss + 0.017 Sabt0.43, (8)
where t is the time (sec). The coefficients in the eq (7) are obtained by the trial-and-error method while solving the system of differential equations (2)-(5) by the finite differences method, and they correspond to the case when the solution is in excellent agreement with the experimental data. The results of the calculations (curves A, B, and C in fig.1) are divided into 3 portions (corresponding to three fractions of minerals) with a somewhat smaller slope but the deviation from the experimental data is comparable with the inaccuracy of the r measurements. Modeling with the dramatically differeing values of Sab and Ssan ( 100 and 0.1 m2 and vice versa) has shown that even in these cases soon after the onset of the reaction rAb and rSan become close in value. Moreover, throughout the way to the equilibrium they differ insignificantly for the both cases as a result of which the times necessary to attain the equilibrium become much the same (fig.2). In the case A the low Ssan value is compensated by the shift of the reaction towards the region of strongly supersaturated solutions where rSan is higher. In the case B the low Sab value is compensated by the shift of the reaction towards the region of strongly undersaturated solutions where rAb is higher.
The reported kinetic features are a consequence of the compensation mechanism the gist of which consists in the mutual influence of rAb and rSan. The influence is by way of activity quotients of the congruent dissolution reactions of albite and sanidine:
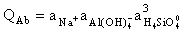(9)
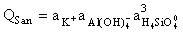(10)
They involve general activities of Al and Si particles i.e. the elements which enter into the equations of the both minerals. The following catenaries explane how an increase in the surface area of one mineral leads to an increase in the precipitation rate of the other:
SAb - rAb - QSan - rSan (11)
Ssan - rSan - Qsan-Qab - rAb (12)
The linkage here is the above mentioned activity quotients.
Fig.1. Dependence of lg r of the Ab San reaction on Lg Sab+lg Ssan.The symbols and the curves stand for the experimental and calculated data, respectively, derived for mineral grains of different sizes d. The open and filled symbols, and the solid and dashed curves correspond to the change in Sab at the constant Ssan value and vice versa. The straight line correspond to the eq. (1).
42
Fig.2. Relationship between the free energies of congruent dissolution reactions of albite and sanidine in the process of the Ab San reaction. The modeling results of the two cases with different Sab and Ssan values (m2) : 100 and 0.1 (curve A), 0.1 and 100 (curve B). The numbers show the time in hours since the onset of the reaction.
References:
Alekseev V.A., Medvedeva L.S., Tatsii Yu.G., Bannykh L.N. Substitution mechanism of albite to sanidine: 2. Replication mechanism.
V.I. Vernadsky Institute of Geochemistry and Analytical Chemistry.
key words [albite sanidine substitution kinetics mechanism]
Polished plates of albite and sanidine (of smaller size) closely adjacent to each other were used in the runs. After the hall a year runs the albite surfaces demonstrated clear impressions of the sanidine plates due to the more intensive proceeding of the substitution reaction of albite to sanidine within the impressions. The shapes of the impressions are suggestive of two ways of pseudomorphous substitution (fig.1b, 1c). The differences between them are most probably due to inhomogeneous distribution along different crystallographic directions in albite of structural defects being active dissolution sites. The presence of the sanidine plate could stimulate that process in accord with the compensation mechanism [1]. It remains to be solved why the action of this mechanism (judging from the sharpness of the impressions) is confined to the region measuring fractions of millimeter. Precisely this kinetic feature ensures the transmission of genetic information on location of defects in a mineral-precursor in the process of pseudomorphic substitution.
Fig.1. Replication mechanism of the substitution of albite (Ab) to sanidine (San). a - initial position of the plates at 300oC and pH 9 in 0.1m KHCO3 solution; b,c - substitution of two types: b- migration of the flat front of the sanidine surface into the albite depth; c- formation of tunnel dissolution pores in albite and the growth of sanidine dendrites in these pores.
Fig.2. Change in the rate of the substitution reaction of albite to sanidine with the changing distance L between the minerals. The L value was given in three ways (see text) and calculated from the eqs.(1) (squares), (2) (rhombs), and (3) (triangles). The triangles apices directed downwards or upwards show the direction of Al transfer. The solid line corresponds to the eq.(4). The dashed line corresponds to the reaction rate in the absence of seed crystals of sanidine.
In order to define the form of the dependence of the reaction rate ( r ) on the distance between the minerals (L) and to understand the nature of this dependence, we have performed additional runs with ground mineral fractions. The L value was given in three ways: 1) by a change of the mineral grain size in their mixture, 2) by rarefying the mixture of albite and sanidine grains with quartz grains, 3) by placing a quartz layer of an appropriate thickness between the albite and sanidine layer. Quartz acted here as an inert rarefier. The runs were conducted at constant surface areas of albite and sanidine equal to 0.28 and 1.1 m2/kg solution.
43
The calculations of L were performed using the following equations with allowance for the above described techniques.
L1 = d/3, (1)
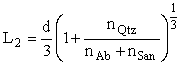(2)
L3 =LQtz + 1/2Lab+1/2Lsan. (3),
here d is the mean grain diameter, n Qtz, nAb, and nSan are the masses of quartz, albite, and sanidine graines; LQtz, Lab, and Lsan are lager thickness of the same minerals.
The results of the runs break down into two portions (fig.2). The horizontal portion on the lower right bear witness to the absence of the dependence for L<1 mm. The r value in this portion is close to the reaction rate in the runs where seed crystals of sanidine were absent (dashed line). The sloping portion on the left indicates an increase of r (mol/kg/sec) with the decreasing L(m) according to the equation
r = 1.4.10-10/L0.42. (4)
We shall consider this dependence in terms of two most recognized hypotheses regarding the stage that controls the reaction rate: diffusional and kinetic. Such a stage is believed to be the diffusion of the dissolved components and elementary reactions on the surface, respectively.
The diffusional hypothesis, as contrasted from the kinetic one, calls for the possibility of the dependence of r on L. Once the distance exceeds the total thickness of the solution diffusional layers near the minerals, its further increase does not lead to a reaction rate decrease any longer since the diffusional distance does not change: a more rapid convective mass transfer occurs between the layers.
We have analysed other criteria for the difference in the both hypotheses: the shape of the kinetic curves, the effect of the solution stirring, the activation energy magnitude, the surface relief of the reacting minerals, the gradients of the elemental concentrations in the solution. It has been found that all the remaining criteria confidentially evidence in favour of the kinetic hypothesis. In terms of this hypothesis one could suppose that between albite and sanidine in our runs there arise surface attraction forces sufficiently great to cause the observable effect. But the action of the surface forces manifests itself only as far as the distance of first microns. This is by 3 orders less than the albite-to-sanidine distance to which the accelerating effect of the sanidine surface on the feldspathization of albite was manifested.
A more actual explanation to the observable dependence can be a slow diffusion of sanidine particles of colloidal size but not of dissolved particles as mentioned afore. Said sanidine particles could form in the solution volume as a result of homogeneous nucleation, then diffuse towards seed crystals of sanidine and fix at their surface. The case in point is microblock growth [2]. It follows from the Einstein- Smoluchouski equation that the diffusion coefficient D is inversely proportional to the diameter of particles d
D = RT/(3
Nd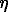
) (5),
here R is the gas constant, T is the absolute temperature, N is the Avogadro constant, h is the viscosity of the medium. This implies that large particles should diffuse slower than the small ones. For example, in order that the diffusion should slow down so that it will be the stage controlling the reaction rate, the size of the diffusing particles must be of the order of 0.1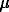 
m.
The importance of the problem considered is that if the microblock growth is the phenomenon typical for the substitution reactions of minerals then the present-day theories of mineral growth from true solutions based on surface geometry are inapplicable to these reactions.
References:
#Baranova N.N., Zotov A.V., Bannykh L.N.1 Stability of gold sulphide species (AuHSo(aq)) and Au(HS)2(aq) at 300, 350oC and 500 bars: experimental study.
key words [gold solubility sulphide species]
Methods. The solubility of metallic gold have been measured at 300, 350oC and 500 bars in water, HCl (0.0002-0.2 m) and NaOH(0.05 m) solutions with H2S concentration of 0.1m. Experiments were carried out in titanium autoclaves. In order to prevent the H2S oxidation the argon was bubbled through solution in an autoclave before sealing. Thioacetic acid amid was used as a source of H2S in 300oC experiments. It was introduced into the autoclave as a weighed solid substance, but hydrolysed under heating:
CH3CSNH2(s) + 2H2O(l) = CH3COONH4(aq) + H2S(g)
For 350oC experiments, hydrogen sulphide solutions were prepared by saturating the acid solutions and water with H2S gas at 1 bar directly in the autoclave. A known amount of metallic aluminium was introduced in the autoclave to evolve hydrogen. Hydrogen pressure in several controlling runs was measured immediately after quenching. These pressure values were in good agreement with those calculated from the reaction of aluminium with water.
Duration of the experiments was 4 to 14 days. After water quenching, total gold concentration was measured by flameless AAS.
# This work was supported by the RFBR (Project N. 97-05-65385)
44
The pH, mHS- and mH2s(aq) values were calculated with the computer code GIBBS (Shvarov, 1992) using the thermodynamic properties of HClo from Tagirov et al (1997) and those for other aqueous species from SUPCRT 92 (Johnson et al., 1992).
Ammonia and acetate ions are formed by hydrolysis of thioacetic acid amid. Ammonia complexes of gold are known to be stable only at very high concentration of NH4NO3 (10m) at 25oC (Skibsted and Bjerrum, 1974). Up to date there is no any information on the stability of gold acetate complexes. During the calculations the possible contribution of ammonia and acetate complexes to total content was neglected.
Results. Experimental data are shown in Fig.1 as a function of calculated pH. Solubility values obtained in this study correspond to total sulphide concentration of 0.1 m, and hydrogen fugacity of 105 and 46 bars at 300 and 350oC, respectively. Fig.1 demonstrates that the AuHSo is the dominate gold species in the solutions of acid pH<3, whereas Au(HS)2 complex became important in low acid and near neutral solutions.
Table. The logarithms of the standard constants of the reactions (1,2) at infinite dilution.
| ToC | logKo(1) | logKo(2) |
| 300 | -5.02+0.25 | -0.25+0.20 |
| 350 | -5.30+0.20 | 0.29+0.30 |
The calculated equilibrium constants for the reactions:
Au(s) + H2S(aq) = AuHSo(aq) + 0.5 H2(g) (1)
Au(s) + H2S(aq) + HS-(aq) = AuHS-2(aq) + 0.5 H2(g) (2)
at 300, 350oC and 500 bars are presented in the Table.
Fig.1. Measured (the symbols) and calculated (the thick lines) gold solubility as a function of pH. The concentrations of gold species ( the thin lines) are calculated using the constants from Table.
Fig.2. Logarithm of equilibrium constants for the reaction (1) as a function of reciprocal temperature at 500 bars. The symbols represent experimental data taken from the references given in the figure.
logKo(1) from Table are shown in Fig.2 together with literature data. It is seen from this figure that logKo(1) values determined in the present study are in good agreement with data of Gibert et al. (in press) and Hayashi and Ohmoto (1991). However, the logKo(2) values (Table 1) are 1-1.5 units higher than that proposed by Shenberger and Barnes (1989); Benning and Seward (1996). The values of Ko(2) may be calculated more precisely using the new values of the first dissociation constant of H2S (Suleimenov and Seward, 1997).
#Sinyakova E.F. Determination of partition coefficients of Pt and light PGE between the phases of the Fe-Ni-S system at 900, 800 and 600oC.
key words [platinum monosulphide melt partition]
(e-mail: sulfide@uiggm.nsc.ru)
The partition of Pt and light PGE (Pd, Rh, Ru) between monosulfide solid solution (mss) and sulfide liquid (L) and their distribution between Fe-Ni sulfide phases during subsolidus crystallization has been investigated in a moderate sulfur part of the Fe-Ni-S system at 900 to 600oC. The FeS-Ni3S2 join with S-content changing from 50 to 40 at.% and two joins with 48 and 51 at.%S are used as macrosystems. The charges of the Fe-Ni-sulfides with the addition of 1 wt.% of Pt, Pd, Rh and Ru, were synthesized using an ampoule method. The samples were melted, slowly cooled (5o/hour) and then annealed at 900, 800 and 600oC. Hexagonal pyrrhotite was used as a fs2 indicator in all runs. The chemical composition of phases was determined using a Camebax electron microprobe. The PGE detection limits were estimated to be 0.02 at.%.
# This work was supported partly by the Russian-French project through grant of RFBR-CNRS N 98-05-22020 and by the RFBR grant N. 98-05-65314
45
Table 1. The average contents of PGE (in at.%) in the coexisting mss, liquid and PGE-alloys depending on fs2 at 900oC.
Section |
FeS-Ni3S2(49-46at.%S) |
48at.%S |
51at%S |
|
Ni/Ni+Fe |
0.1 |
0.2-0.4 |
0.4-0.65 |
>0.65 |
lgfs2 |
-6.5 |
-6.5 -4.5 |
-4.5 -2.4 |
>-2.4 |
Pt |
Pt0.44Fe0.43Ni0.13 |
Pt0.51Fe0.38Ni0.11 |
0.5 in L |
0.2 in S-mss |
|
0.04 in L |
0.15 in L |
or Pt0.65Fe0.30 Ni0.05 |
up to 3 in L |
Pd |
no data |
0.015 in mss |
0.05 in mss |
0.15 in S-mss |
0.55 in L |
0.5 - 1.3 in L |
1.9-6.5 in L |
||
Rh |
Fe0.51Rh0.29Ni0.20 |
0.15 in mss |
0.6 in mss |
0.74 in S-mss |
0.02 in mss,0.86 in L |
0.4 - 1.0 in L |
0.5 in L |
0.15 in L |
|
Ru |
Ru0.60Fe0.35Ni0.05 |
0.5 in mss |
0.9 in mss |
2.3 in S-mss |
0.08 in mss,0.14 in L |
0.2 in L |
0.15 in L |
0.02 in L |
Table 2. Experimental results for metal partition coefficients mss / liquid at 900oC
lgfs2 |
<-6.5 | 6.5-4.5 |
4.5-2.4 |
>-2.4 |
Pt |
< 0.01 |
< 0.01 |
< 0.01 |
0.04+0.01 |
Pd |
no data |
0.025+0.005 |
0.045+0.025 |
0.045+0.025 |
Rh |
0.02 |
0.35+0.15 |
1.5+0.5 |
4.9 |
Ru |
0.6 |
1.75+0.75 |
5+1 |
35+5 |
Tables 1, 2 illustrate the relationship between the partition coefficients of metals for mss/sulfide liquid and S-fugacity, depending on the starting S-content in the system and the Ni/Ni+Fe ratios at 900oC. It should be noted that in our experiments nickel prefers sulfide liquid rather than mss, while iron enriches mss rather than liquid. The partition coefficients for Ni vary from 0.2 to 0.9 and depend on the Ni/Ni+Fe ratio in the initial charges, while iron has the partition coefficients of 1.57± 0.12 under different conditions.
Pt shows the minimum affinity to sulfur in comparison to light PGE. It crystallizes from Fe-rich sulfide melt in the form of tetraferroplatinum Pt(Fe,Ni) together with Fe-rich mss at low S-fugacity of FeS-Ni3S2 section (lgfS2 = -4.5) or in the form of isoferroplatinum Pt3(Fe,Ni) together with Fe(and S)-rich mss at high fs2 of the section with 51 at.% S (at lgfs2 from –3 up to –2.4). At crystallization of Ni-rich melts, Pt is preferentially enriched in sulfide liquid rather than mss.
Pd is concentrated preferably into sulfide liquid with respect to crystallizing mss. The Me/S ratio of this liquid corresponds to (Ni,Fe,Pd)3-XS2+X. The Pd-contents of the liquid and mss increase with increasing sulfur fugacity in the system.
The distribution of Rh between the phases depends strongly on the fs2 in the system. The intermetallic phase ferrorhodium (FeRh) is formed only in maximum Fe-rich compositions of the FeS-Ni3S2 section together with Ni-pyrrhotite containing up to 2.1 at.% Ni at low sulfur fugacity (lgfs2<-6.5). Under this conditions Rh partitions between FeRh and sulfide liquid. At the increase of lgfs2 up to –5 it partitions between the Fe-mss and liquid, favoring the liquid. The Rh behavior changes at high S-fugacity (lgfs2>-3) in the Ni-rich compositions of the system (Ni/Ni+Fe>0.5), where it enters mss and liquid proportionally or it enriches mss rather than sulfide liquid.
Ruthenium is preferably enriched in mss under various conditions investigated. Its partition coefficients for the mss/liquid range from 1 to 6 at the lgfs2 variation between –6.5 and –2.4. Under the conditions of higher fs2 Ru partitions preferentially in S-rich mss in comparison to the liquid and has the partition coefficient of about 35. Ru gives alloy phase only under the conditions, similar to those where the Rh-alloy phase is formed.
The decrease of temperature leads to appearance of mss associations with hzss (heazlewoodite solid solution (FexNi 1-x)3+-YS2) at 800 and with pentlandite (Pn) at 600îÑ. A specific feature of Pt behavior at these temperatures is its isolation as independent minerals: tetraferroplatinum, isoferroplatinum and cooperite. The conditions of their existence are determined by S-fugacity as well. The behavior of light PGE differs from those for Pt because of their distribution between the main sulfide phases. At 800oC light PGE preferentially concentrate in mss and hzss solid solutions. Pd prefers to be dispersed in hzss, in the lgfs2 range from –6.8 up to –3. At increasing sulfur fugacity, Pd partitions between mss and hzss, or concentrates in S-rich mss. At 600oC, it passes into pentlandite, which forms as a result of peritectic reaction between hzss and mss. The association of sulfide phase (Pd,Ni,Fe)S with Ni-rich mss appears at lgfS2 > -6.4 and of (Pd,Fe,Ni)16S7 with Fe-rich mss at the lgfs2 nearly –7.5 (section with 51 at.% S). Rh and Ru demonstrate the high affinity to sulfur and accumulate only in sulphide solid solutions (in mss at high temperatures as well as in mss and hzss at moderate ones). Under the same conditions, Rh enters mss and hzss proportionally while Ru prefers to be in mss. Below 600°C, pentlandite becomes the principal bearer of this elements with formation of p-phase type containing up to 4 at.% Rh and up to 5.4 at.% Ru.
46
The present experimental data provide a possibility to trace the dynamic of concentration behavior of light PGE from mss+liquid-equilibrium up to pentlandite appearance. It is shown, that the partition coefficients for PGE depend on S-fugacity, i.e. S-content in the system and Ni/Ni+Fe ratio. It is recognized that Pt is a component with metallic properties because of its early crystallization from Fe-Ni-sulfide melts in the form of intermetallic phases. The Pt-tendency to form intermetallic phases is preserved at temperature decrease up to the appearance of pentlandite associations. Light PGE are rather chalcophile, because they prefer sulfide phases to intermetallic at various steps of crystallization of Fe-Ni-sulfide melt. Pd prefers Ni-rich sulfide phases. It separates into the Ni-rich liquid to a maximum degree at 900oC and as temperature further decreases it prefers Hzss, Pn, the S-rich mss and its proper sulfides. Rh behavior is greatly dictated by a change of the above factors. During high-temperature stage of crystallization of the Fe-rich melt, Rh prefers liquid as compared to mss. The more Ni-rich melts under the conditions of greater fs2 separate Rh into forming mss rather than into liquid. As temperature decreases, Rh tends to be distributed between the mss and hzss or between mss and Pn proportionally. Ru enriches the mss being in equilibrium with the liquid, hzss or Pn. The obtained experimental data may provide the quantitative ground for the hypothesis of fractional crystallization of sulfide ore melts.
#Pal'yanova G.A., Konnikov E.G., and Kolonin G.R. Thermodynamic analysis of a possible effect of water and carbonic acid on stability of pyrrhotite under pre-melting conditions.
2 Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, Moscow Region
key words [ pyrrhotite water carbon dioxide interaction ]
The thermodynamic calculations of the phase stability in FeS-Ni-O, FeS-Ni-H2O, and FeS-Ni-H2O-CO2 systems in the 1000-1160oC temperature range and pressure of 1000 bar were calculated by the Selektor-S program (developed by I. G. Karpov and K.V.Chudnenko) using the thermodynamic data available from the databases c-sprons and g-sprons, which are added new data from paper (Robie, Hemingway, 1995). The probability of the formation of the following solid phases and gases at the aforementioned PT parameters was taken into account in the calculations: FeO, Fe3O4, Fe, FeS, Ni, NiO, SO2, H2S, S2, H2, O2, CO2, and CH4. The real ratios of pyrrhotite, water and carbonic acid in the experiments performed by one of the authors under similar thermodynamic conditions were also taken into account. Unlike the experiments, troilite was accepted as the starting iron monosulfide, and the molar fraction of nickel with respect to troilite was equal to 0.001. The calculation of the FeS-Ni-O system was performed when 0.00005 mol O2 was additionally introduced.
As can be seen from the calculated results presented in table, pyrrhotite in the presence H2O and H2O + CO2 decompose partially to form magnetite. Among gases along with water and carbonic acid, H2, H2S, S2, and SO2 are stable under these PT conditions. It also follows from the data in table and Fig. 1 that the molar fraction of magnetite increases as the amount of the aqueous fluid in the system and temperature increase. The carbonic fluid also favours the decomposition of pyrrhotite to form magnetite, but to a lower extent. The oxygen fugacity increases distinctly, which is evidently a reason for the partial oxidation of iron in pyrrhotite. Oxygen from the aqueous and water-carbonate fluids is also consumed in the oxidation process, which is indicated by a decrease in the concentrations of H2O and CO2 and a simultaneous increase in sulfur-containing gas phases (Fig.2), whose sulfur is liberated from pyrrhotite when iron is transferred to magnetite. Hydrogen released in the oxidation of iron with water also partially binds sulfur to form H2S.
Fig.1. The mole abundance of magnetite formed during interaction of pyrrhotite with water and water-carbon dioxide fluid at different temperatures; the amount of fluids is in wt%
# This work was supported by the RFBR (Project N. 96-05-64714)
47
Fig.2. The gas phase composition (wt%) in the system ''pyrrhotite + H2O + CO2'' vs temperature
Table. Amount of magnetite (molar fractions) and composition of the gas mixture (wt.%) formed during the interaction of pyrrhotite with aqueous and water-carbonic acid fluid (H2O : CO2 = 1 : 1) at P = 1000 atm and buffer NNO
Starting compounds |
Products of interaction |
|||||||||||
| ToC | FeS | H2O | CO2 | Magnetite | H2O | H2 | H2S | S2 | SO2 | CO2 | CH4 | -lgfO2 |
| 1160 | 0.9 | 0.488 0.244 |
0 0.1 |
0.016 0.008 |
76.56 38.97 |
1.39 0.77 |
10.23 5.08 |
2.28 1.33 |
9.53 5.29 |
- 48.56 |
- 0 |
6.84 6.91 |
| 1080 | 0.9 | 0.488 0.244 |
0 0.1 |
0.013 0.006 |
81.96 41.61 |
0.99 0.54 |
9.00 4.45 |
1.41 0.83 |
6.63 3.68 |
- 48.88 |
- 0 |
7.67 7.74 |
| 1000 | 0.9 | 0.488 0.244 |
0 0.1 |
0.010 0.005 |
86.37 43.74 |
0.68 0.37 |
7.77 3.84 |
0.82 0.48 |
4.36 2.43 |
- 49.14 |
- 0 |
8.62 8.68 |
| 1160 | 0.8 | 0.976 0.488 |
0 0.2 |
0.032 0.017 |
76.56 38.97 |
1.39 0.77 |
10.23 5.08 |
2.28 1.33 |
9.53 5.29 |
- 48.56 |
- 0 |
6.84 6.91 |
| 1080 | 0.8 | 0.976 0.488 |
0 0.2 |
0.025 0.013 |
81.96 41.61 |
0.99 0.54 |
9.00 4.45 |
1.41 0.83 |
6.63 3.68 |
- 48.88 |
- 0 |
7.67 7.74 |
| 1000 | 0.8 | 0.976 0.488 |
0 0.2 |
0.019 0.010 |
86.37 43.74 |
0.68 0.37 |
7.77 3.84 |
0.82 0.48 |
4.36 2.43 |
- 49.14 |
- 0 |
8.62 8.68 |
| 1160 | 0.7 | 1.464 0.732 |
0 0.3 |
0.050 0.025 |
76.56 38.97 |
1.39 0.77 |
10.23 5.08 |
2.28 1.33 |
9.53 5.29 |
- 48.56 |
- 0 |
6.84 6.91 |
| 1080 | 0.7 | 1.464 0.732 |
0 0.3 |
0.038 0.019 |
81.96 41.61 |
0.99 0.54 |
9.00 4.45 |
1.41 0.83 |
6.63 3.68 |
- 48.88 |
- 0 |
7.67 7.74 |
| 1000 | 0.7 | 1.464 0.732 |
0 0.3 |
0.029 0.015 |
86.37 43.74 |
0.68 0.37 |
7.77 3.84 |
0.82 0.48 |
4.36 2.43 |
- 49.14 |
- 0 |
8.62 8.68 |
48