Hydrothermal processes, fluid systems, metasomatism
#Konnikov E.G. Influence of water-carbonate fluid on the melting temperature of pyrrhotite.
key words [influence pyrrhotite melt carbon-dioxide]
# This work was supported by the RFBR (Project N. 97-05-64714)
28
Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, Moscow Region
A series (16) experiments on studying the influence of CO2 on the melting temperature of iron monosulfide was performed. To compare these experiments with those previously performed in the Po--H2O system, they are carried out at similar thermodynamic parameters, namely P = 1000 atm, T = 1000-1150oC, and fO2 was monitored by the NNO buffer. The Fe0.94S powder of artificially synthesized pyrrhotite was used as the blend. The content of fluid varied from 5 to 30 wt.% of the weight of pyrrhotite, and it was obtained by the thermal decomposition of oxalic acid H2C2O4.2H2O resulting in the formation of water-carbonate mixture with the ratio of components 1 : 1.
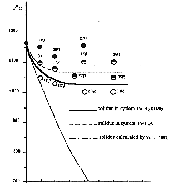
The experiments showed that when iron monosulfide is melted with the CO2 + H2O mixture, the temperature of its solidus decreases by 120-130oC as compared to the "dry" solidus of pyrrholite with the same composition at the concentration of a water-carbonate mixture of 15-20 wt.% (see figure).
The further increases in the fraction of this fluid does not lead to a decrease in the melting temperature of pyrrhotite. The quenching products of the melted phase contains, along with pyrrhotite, a new phase magnetite, which forms graphic concretions with iron monosulfide. The amount of magnetite increases proportionally to an increase in the content of the water-carbonate mixture in the system initial for melting, which allows one to relate the decrease in the melting temperature of pyrrhotite to the oxidizing effect of the fluid. This conclusion is confirmed by similarity of the experimental melting temperatures of the pyrrhotite-fluid system to the calculated solidus temperatures of quenching graphic concretions of pyrrhotite and magnetite according to the Shreder equation and thermodynamic studies of Po + H2O + CO2 by the Selektor-S program (developed by G. I. Karpov and K. V. Chudnenko) performed by G. A. Pal'yanov in JGGM SB RAS (Novosibirsk).
Since the decrease in the melting temperature of pyrrhotite with the water-carbonate fluid is 30-40oC higher than that under similar conditions of melting with neat H2O (Konnikov, 1997), we may conclude that CO2 also decreases the melting temperature of sulfides, unlike silicate systems, whose solidus temperatures increase in the presence of carbonic acid.
Tikhomirova V.I., Akhmedzhanova G.M., Chichagov A.V., and Samokhvalova O.L. Hydrothermal synthesis of aurostibite (AuSb2) and sperrylite (PtAs2).
key words [aurostibite sperrylite hydrothermal synthesis ]
Under natural conditions, sperrylite and aurostibite are encountered as individual minerals on contacts with melts of noble metals in ultrabasic rocks, being the result of the high-temperature evolution of the magmatic process. Therefore, the synthesis of these compounds from elements requires high temperatures and, in addition, the melting process should be performed in closed furnaces with an inert atmosphere preventing evaporation and oxidation of the components, especially in the case of arsenic. In the phase diagrams of the Au-Sb and Pt-As systems, the melting temperature for aurostibite is 460oC, and that for sperrylite is 1510oC.
On the other hand, the authors of [1] emphasize the role of hydrothermal solutions, especially enriched in volatiles, in the formation of several intermetallides of noble metals at specific stages of the ore process. Third, in the practice of electrochemical studies during reduction of arsenic compounds on the platinum or gold electrodes at the corresponding reduction potentials, surface compounds of arsenic are formed, which is detected by the potential shift of their subsequent anode oxidation in curves I- in the method of inversion voltammetry [2].
in the method of inversion voltammetry [2].
Therefore, to develop model conditions of hydrothermal synthesis, we created the reduction medium in situ by the introduction of metallic powdered aluminum in aqueous solutions of dilute hydrochloric acid (0.01-0.1 N), which were placed in autoclaves of the VT-8 titanium alloy. The following reaction with water occurs at 300oC and 500 atm:
2Al + 4H2O = 2Al(OOH) + 3H2 (1)
which makes it possible to calculate the stoichiometric hydrogen release, its fugacity, and fugacity with respect to oxygen in order to compare which natural buffers are modeled in such a way.
In experiments, platinum or gold plates were hanged up in the upper part of the autoclave, and crystals of arsenic or antimony in the form of metal were placed in a special container. Prior to experiments, dissolved oxygen was removed from solutions of hydrochloric acid (0.01 and 0.1 N) by bubbling of an inert gas.
This statement of experiments allowed us to observe surface compounds of platinum with arsenic and those of gold with antimony on the platinum and gold (in particular series of experiments) surface. These compounds are stable in air and rather dense, which allowed their analysis by X-ray phase and X-ray spectral methods with a defocused probe. They were identified as sperrylite (PtAs2) and aurostibite (AuSb2) from reflections of the X-ray phase analysis.
29
Fig.1.
Fig.2.
Fig.3.
To understand the mechanism of the synthesis, let us consider the redox conditions in the experiment and concentrations of the components. It is known that at the experimental parameters (300oC and 500 bar), H3AsO3 (by the data in [4]) and Sb(OH)3 [5] are the predominant soluble forms of arsenic and antimony in the sulfide-free system. In a weakly acidic medium of HCl (0.01 and 0.1 N) the concentration of arsenic is n.10-2 M in the solution in equilibrium with metallic arsenic and concentration of antimony is approximately the same (10-3 M) at the strongly reductive medium with the hydrogen fugacity of 132 bar (logfH2 = 2.12).
The corresponding value of the oxygen fugacity is logfO2 = -47.7. The calculation was performed with the figures of the SUPCRT-92 database at 300oC and 500 bar. For this oxygen fugacity [4], arsine can be in equilibrium with metallic arsenic.
The thermodynamic calculation from the same database for the possible reaction of high-temperature hydrolysis with partition:
As + 3H2O = AsH3(aq) + H3AsO3(aq) (2)
gives Kequiv = 10-16.5 for 300oC and 500 bar.
This value of the equilibrium constant of reaction (2) makes improbable the considerable concentrations of arsine in the solution, if there are no additional catalytic effects [6]. This arsine concentration is sufficient if the solubility products of the arsenides formed are rather low. Platinum potential, if calculated as hydrogen electrode at 300oC and given hydrogen fugacity, is (-0.354V) rel. n. hydrogen electrode. At this the reduction of three valence arsenic or antimony from the solution as well as catalytic decay of arsine on the surface leading to sperrylite formation by the reaction: Pt + 2AsHzaq +1.5O2 = PtAs2 + 3H2O. The fact that the growth of the compounds forming depends on the sublayer structure counts in favour of the last catalytic mechanism. But this is the subject for further investigations. In solving the problems related to the role of the sublayer crystal structure where epitaxial films of a new compound may grow, great possibilities are provided by the software 'CrystPic', which in terms of the system 'Mincryst' [6] allows measure the lengths of intertatomic bonds in the lattice, distinguish plane fragments.
30
Fig.1 shows the general view of the cell of sperrylite crystallizing within the pyrrite structural type, the same as aurostibite. Figs.2 and 3 give different projections of sperrylite for the plane fragments with nkl (III) and (200). The comparison of real X-ray patterns with reflexes from ideal structures can give the picture of mineral growth in the real geochemical conditions.
References:
#Korzninskaya V.S., Zaraisky G.P. Calcium to - manganese ratio in a chloride fluid in equilibrium with scheelite-hubnerite association at T=300-600oC, P=1 kbar.
key words[scheelite hubnerite fluid experiment]
The scheelite-hubnerite equilibrium in chloride solutions has been experimentally studied at temperatures 300,400, 500 and 600oC, pressure 1 kbar, and oxygen fugacity controlled by solid Ni-NiO and Fe-FeO buffers.
The experimental technique is analogous to that described earlier for the scheelite-ferberite equilibrium [1]. The initial concentration of CaCl2 and MnCl2 was varied broadly from 10-4 to 1 mole/kg H2O in order to provide approaching the equilibrium from 'above' and 'below' in the range of different concentrations. The duration of the runs was from 16 to 8 days. After the runs were completed, the solutions were quenched to room temperature for 5-7 min under a pressure. The solution being examined was separated from the mineral charge with a filter after the run. Calcium in the solution was determined on an atomic-absorption spectrophotometer AAS (Carl Zeiss Iena), and manganese on a spectrometer Spekol-11 using potassium metaperoiodate (KJO4) [2]. The examined reaction can be written as
CaWO4 + MnCl2(aq) = MnWO4 + CaCl2(aq) (1)
Scheelite hubnerite
In experiment solid CaWO4 and MnWO4, synthesised by us under hydrothermal conditions, in amounts of 15 mg each, and aqueous chloride solutions (CaCl2, and MnCl2) of a certain concentration in amounts of 250-450 mg, depending on the temperature, were placed together in a hermetically sealed gold capsule at a preset oxygen fugacity controlled with an inner buffer. The amount of the buffer was 500 mg, and its volume exceeded that of the mineral charge by many times. The equilibrium position was registered only in the case where both scheelite and hubnerite were present in the run products. In individual runs only one mineral was a charge constituent. As a rule, this is characteristic of solutions having a high initial concentration of one of the components (0.1-1 m) at a low concentration of the other which is attributed to a deficit in the buffer capacity of the solid charge required to maintain the equilibrium mCaCl2:mMnCl2 in the solution.
The results of the runs throughout the temperature and solution concentration ranges studied are illustrated in the diagram for two oxygen buffers Ni-NiO (shaded figures) and Fe-FeO (unshaded figures). The uncertainty region due to spread in experimental points is maximally 0.2-0.5 as great as the logarithmic value of the concentrations. As seen from the diagram there is a positive dependence of the scheelite-for hubnerite substitution reaction on the temperature. The effect of fO2 variation (within Ni-NiO and Fe-FeO buffers) on the equilibrium position is in sufficient.
Under the assumption that the activities of the solid phases are unity and the preferential occurrence of the dissolved forms of calcium and manganese at high temperatures are neutral chloride complexes CaCl2o and MnCl2o, one can write the following approximated relationship for the thermodynamic and concentrational equilibrium constants of the reaction (1):
 (2)
(2)
where mCaCl2(aq) and mMnCl2(aq) correspond to m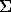 Ca and m
Ca and m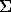 Mn, measured after the run in quenched solution.
Mn, measured after the run in quenched solution.
Fig.1. Ca-to-Mn concentrations ratio in the fluid in equilibrium with the hubnerite-scheelite association for temperatures 300-600oC for Ni-NiO and Fe-FeO buffers.
# This work was supported by the RFBR (Project N. 97-05-64709)
31
Fig.2 Temperature dependence of the hubnerite-scheellite equilibrium constant
The dependence of the equilibrium constant of the scheelite-hubnerite reaction on the temperature has been plotted (see fig.2). For plotting this diagram we used mean values of the constants calculated from the experimental data obtained throughout the range of chloride concentrations at 300, 400, 500, and 600oC. The temperature dependence is expressed by the equation of the form
Lg Kp = 2729/T, K 3.2940 (+ 0.1504) (3)
where shown in brackets is the averaged error of the lgKp determination for the studied temperature range (300-600oC) and for the both buffers.
Table 1 gives the Ca/(Ca+Mn) values for the solution in equilibrium with the scheelite-hubnerite association under the pressure 1 kbar, (our experimental data and the scarce results of the authors [3,4]).
The fluid composition was computed using the GIBBS algorithm (Ju.V. Schvarov) in conformity with the experimental conditions. The computation has made it possible to evaluate the free energy of hubnerite (MnWO4) (see table 2) from the independent equilibria.
CaWO4 + Mn2+ = MnWO4 + Ca2+ (4)
CaWO4 + MnCl+ = MnWO4 + CaCl (5)
CaWO4 + MnCl20 = MnWO4 + CaCl2 (6)
Table 1. 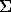 Ca/
Ca/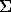 (Ca+Mn) values in the solution in equilibrium with scheelite-hubnerite associations at P=1 kbar from the data of different authors.
(Ca+Mn) values in the solution in equilibrium with scheelite-hubnerite associations at P=1 kbar from the data of different authors.
ToC |
|
||
Our data |
Uchida et al., 1989 |
Baumer et al., 1985 |
|
Hub |
Hub |
Hub |
|
300 |
0.96 |
- |
- |
400 |
0.89 |
0.64 |
- |
500 |
0.61 |
- |
- |
600 |
0.37 |
0.32 |
0.33 |
Table 2. Thermodynamic properties of hubnerite (MnWO4), P=1 kbar
Mineral |
Thermodynamic constant |
Temperature |
||
300oC |
400oC |
500oC |
||
Hubnerite |
LgK1 |
2.774 |
2.604 |
0.377 |
LgK2 |
0.551 |
0.374 |
-1.583 |
|
lgK3 |
4.002 |
3.680 |
1.334 |
|
-Gf,t kcal/mol |
305.636 (+ 0.005) |
311.680 (+ 0.003) |
311.075 (+ 0.005) |
|
where: lgK1 = lgmCa2+ /lgmMn2+ for the equilibrium
CaWO4 + Mn2+=MnWO4+Ca2+
lgK2 = lgmCaCl+ /lgmMnCl+ for the equilibrium
CaWO4 + MnCl+=MnWO4+CaCl+
lgK3 = lgmCaCl20 /lgmMnCl20 for the equilibrium
CaWO4 + MnCl20=MnWO4+MnCl20
References:
#Dadze T.P., Akhmedzhanova G.M., Kashirtseva G.A. Solubility of gold in sulfide-containing aqueous solutions at T = 300oC.
key words[gold solubility fluid sulphide]
In this work, we present the data on the experimental determination of solubility of gold at T = 300oC, P = 300 atm, Psat=85 atm, and pHstart.sol. = 7.4, which (Ph) was achieved by the addition of a solution of NaOH with a low concentration. The concentration of H2S varies in a wide range from 5.10-2 to 0.7 m/l. The pH value of the solution with the content of 0.05 m H2S measured after quenching was 4.15, and for a solution with 0.7 m H2S, it was 4.0, and that calculated by the "Gibbs" program (Shvarov, 1982) for the system Au-S-Na-H-O at experimental parameters does not virtually change with the concentration H2S from 0.05 to 0.7 m and equals 5.5.
The experiments were carried out in titanium 20 cm3 autoclaves. A gold (99.99) plate with a size of 10.5.0.1 mm was hanged on an obturator in the upper part of the autoclave. Thioacetamide (CH3CSNH2) was used as the H2S source. In aqueous solutions, it is slowly (or rapidly in the presence of acids and alkalis) hydrolyzed to yield H2S.
# This work was supported by the RFBR (Project N. 97-05-64646)
32
Fig. 1. Dependence of the solubility of gold on the concentration of H2S at 300oC by experimental data.
Fig. 2. Dependence of the solubility of Au on the concentration of H2S at 300oC: 1 - Psat; 2 - 300 atm (our data); 3- Psat (Wood et al., 1987); 4 - Psat (Hayashi and Ohmoto, 1991).
The duration of experiments was from 3 weeks to 1 month. Autoclaves were quenched with a cold running water for 5-7 min. Autoclaves with the content of H2S higher than 0.5 m were cooled with a water-ice mixture to prevent splashing out of the solution because of excessive pressure due to the gas released. Gold was analytically determined from the hydrochloric medium after the quantitative collection of gold transferred to the solution during the experiment by the atomic-absorption method in the acetylene-air flame on an AAS-N instrument at the wavelength of 242.8 nm.
In the present time, the most important form of gold transfer under hydrothermal conditions in a wide pH range (2-8.5) is the hydrosulfide complex Au(HS)-2 formed in the reaction:
Au + H2S(l) + HS- = Au(HS)-2 + 1/2H2(g) (1)
On the other hand, the formation of complexes Au(HS)o [Seward, 1973; Renders, Seward, 1989] and HAu(HS)o2 [Wood et al., 1987; Hayashi, Ohmoto, 1991] is assumed in acidic solutions:
Au + H2S(l) = Au(HS)o + 1/2H2(g) (2)
Au + 2H2S(l) = HAu(HS)o2 + 1/2H2(g) (3)
The results of our studies are presented in Fig. 1 in coordinates log mH2S log mAu. It is seen that the distinct dependence of the solubility of gold on the H2S concentration is obtained; the gold concentration in the solution increases as the H2S content increases. At 300oC, this dependence is expressed by the first-power equations:
lg mAu = -2.65116 + 1.48774.lgmH2S +0.004
(P=85 atm)
lg mAu = -3.27197 + 1.45035.lgmH2S +0.17
(P=300 atm)
The error was calculated by the least-squares method, the calculation covers 95%, 87% of all experimental points. The slope factors of the curves obtained in our curves equal to 1.48, 1.45 suggest that dissolvation of gold under conditions of our experiment with formation of two compexes by the reaction:
2Au + 3H2S(l) + HS- = Au(HS) -2 + HAu(HS)o2 + H2(g)
The results of our studies compared to the data calculated by the "Gibbs" program [Shvarov, 1982] from the equilibrium constants of reaction (3) using the data of [Wood et al., 1987; Hayashi, Ohmoto, 1991] are shown in Fig. 2 in coordinates log mH2S lg mAu. Calculated value of oxygen fugacity at the experimental parameters practically does not change (log fO2 = -34).
Thus, the results of the experimental studies confirm that the solubility of gold depends on the concentration of H2S in the system and occurs in weakly acidic solutions with the formation of the neutral HAu(HS)o2 and Au(HS)-2 complexes.
References:
33
#Abramov S.S. Thermodynamic modelling of stability of biotite (annite-phlogopite) in association with feldspar, magnetite, fayalite, pyrrhotine, and ilmenite in a C-O-H-S-F- fluid within 427-1027oC.
key words [biotite fluid stability]
Isopleths of annite has been calculated for the reactions
Ann = Kfs + Mag + H2 (R1)
2Ann + 3Qtz = 2Kfs + 3 Fay + 2H2O (R2)
xAnn + 1.5S2 + xKfs + 3Poss (R3)
Ann + 0.75O2 = Kfs + 1.5 Hem (Ilm) + H2O (R4)
in equilibrium with C-O-H-S-F fluid (fig.1,2).
A new algorithm has been proposed for the calculation of the compositions of the C-O-H-S-F (Cl) gas mixture saturated and undersaturated in graphite. As contrasted from ref. [1] where the system of equations models the two-phase graphite-fluid equilibrium, in this work it is made up so as to calculate homogeneous fluid reactions. This solution is then modified for graphite-fluid, fluid-arbitrary mineral association equilibria. The proposed algorithm can be used to calculate oxygen fugacities in the reactions rock-COHSF fluid that involves 19 gas particles. The thermodynamic data for the fluid components were borrowed from ref. [2]. The fugacity coefficients for H2O and H2 were calculated from [1,3] those for O2, CO2, CO, CH4, COS , SO2, S2, H2S from [4]. The fugacity calculations for the remaining components were based on the ideal gas model. The thermodynamic constants of annite were calculated using the experimental data of ref. [5]. The calculations were performed by the model of biotite solid solution according to [6] supplemented by the dependence of (Fe2/Fe3+Fe2) in biotite on fH2 in the fluid [7]. The isopleths of annite in equilibria with graphite, feldspar, fayalite, quartz and/or pyrrhotine in the T-fO2 space have a pronounced thermal stability maximum (fig.2) complying with the equilibrium with the graphite-saturated COHSF fluid having a maximal molar fraction of water [8].
Fig.1. Isopleths of annite (xann = 0.9, 0.6, 0.3) in reactions R1 and R2 and COH fluid.
Fig.2. Isopleths of annite (xann=0.9, 0.6, 0.3) in reactions R1 and R2 and COH fluid in equilibrium with graphite.
References:
##Akinfiev N.N. Thermodynamic description of dissolved nonelectrolytes in a broad range of the parameters of state.
key words [dissolved nonelectrolite thermodynamic properties calculation]
An approach has been proposed for the description of thermodynamic properties of aqueous nonelectrolytes (Ar, H2S, CO2). The approach is based on the 'precise' multiparametric Hill equation [1] for solvent and the formalism closely resembling the virial equation of state. So, the
# This work was supported by the RFBR (Project N. 98-05-64052)
## This work was supported by the RFBR (Project N. 98-05-64234)
34
standard chemical potential of a dissolved particle at the given temperature T and pressure P is written in the form
 ,
,
where 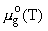 is the chemical potential of the corresponding pure gas under standard pressure,
is the chemical potential of the corresponding pure gas under standard pressure, 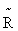 = 1.9872 cal/(mol.K) is the universal gas constant, f1o and
= 1.9872 cal/(mol.K) is the universal gas constant, f1o and  1o are the fugacity and density of a pure solvent (H2O), and
1o are the fugacity and density of a pure solvent (H2O), and  B
B = B12-B1 is the difference between the virial coefficients characterizing the interactions nonelectrolyte H2O and H2O-H2O. By differentiating this equation with respect to pressure and temperature, we obtain the expression for limiting molal thermodynamic characteristics of the dissolved component:
= B12-B1 is the difference between the virial coefficients characterizing the interactions nonelectrolyte H2O and H2O-H2O. By differentiating this equation with respect to pressure and temperature, we obtain the expression for limiting molal thermodynamic characteristics of the dissolved component:
volume 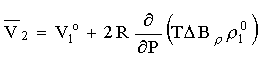
enthropy 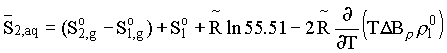 and specific heat
and specific heat 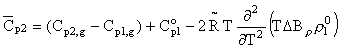
Here the index 'i' is pertinent to the solvent at the pressure and temperature, and the index 'g' is pertinent to the dissolved component in the state of ideal gas at the same temperature and standard pressure.
To describe the temperature dependence of  B
B three-parameter equation of the form
three-parameter equation of the form 
 is proposed.
is proposed.
The empiric parameters  1,
1,  2,
2,  3 can be reconstructed from the experimental data for the Henry gas constant in the subcritical temperature region. These parameters are given in the table.
3 can be reconstructed from the experimental data for the Henry gas constant in the subcritical temperature region. These parameters are given in the table.
| Gas |  1 1 |  2 2 |  3.102 3.102 |
| Ar | 2.27132 | 0.86 | -1.50352 |
| H2S | 1.5000 | 0.55 | -0.4 |
| CO2 | 1.76612 | 0.75 | -1.23586 |
So the knowledge of the thermodynamic characteristics of pure gas together with the three parameters of the model  1,
1,  2,
2,  3, enables one to describe the complete set of thermodynamic properties of a dissolved component (chemical potential, enthropy, molar volume, and specific heat) in a broad range of temperatures (0-500oC) and pressures (1-2000 bar) involving the near-critical region. As an illustration the figures give the calculated (lines) and experimental (dots) values of various thermodynamic properties of dissolved hydrogen sulphide.
3, enables one to describe the complete set of thermodynamic properties of a dissolved component (chemical potential, enthropy, molar volume, and specific heat) in a broad range of temperatures (0-500oC) and pressures (1-2000 bar) involving the near-critical region. As an illustration the figures give the calculated (lines) and experimental (dots) values of various thermodynamic properties of dissolved hydrogen sulphide.
Reference:
35
Gorbunov V.Yu. Modelling of redox state of sulfur in hydrothermal solutions.
key words [pitch blende sulfur oxidation calculation]
V. I. Vernadskii Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences
In the present time, it is established that the formation of pitchblende ores in almost all deposits in the world occurred at the temperature close to 200oC. This indicates to the internal (for uranium-bearing solutions) temperature reason for ore deposition. Mineralogical studies show that sulfides, sulfo salts are deposited along with pitchblende, and carbonates (ankerite, calcite) are often present.
The experimental works of S. D. Malinin and N. I. Khitarov (1965) and then studies of R. P. Rafal'skii (1985) showed that the lower limit of reduction of sulfate sulfur to sulfide sulfur is 200oC in near-neutral solutions and 250oC in acidic solutions. According to the experimental data (Giggenbach, 1977), at temperatures lower than 200oC, oxidation of sulfide sulfur is strongly suppressed and occurs not to SO42-, but to the intermediate forms of oxidation of sulfur between S2- and S0.
To estimate the effect of the kinetic factor on the redox interaction of different forms of sulfur, the thermodynamic modeling of the process was performed at 200oC under hydrothermal solutions in the system corresponding to the natural hydrothermal uranium-molybdenum system.
The main task of the modeling performed was the consideration of possibilities of changing valence states of sulfur to form all known forms of occurrence of this element in solutions and minerals and elucidation of conditions of existence of sulfur in the sulfide and disulfide forms only. The amount of sulfur, which was in solution in the sulfate form, was replaced by artificial anions with the physicochemical properties similar to those of the forms of sulfuric acid in solution. This was performed to retain complex formation and acidity in the solutions. These anions had no effect on the redox conditions in the system. The choice of the state of the system at which this replacement was performed is caused by the maximum amount of the sulfate ion within the stability field of molybdenite.
The results of the theoretical experiments show that the following occurs when the mechanism of oxidation of sulfide sulfur is changed (sulfide/sulfate by sulfide/disulfide):
- a sharp increase in the stability field of pyrite and molybdenite;
- a shift of the redox parameters of the system to a more reduced region.
The estimation of possibilities of formation of anhydrite in equilibrium with calcite in a similar system showed:
- when S2- is oxidized to S6+, anhydrite stable in association with pyrite and magnetite should be formed in equilibrium with calcite.
The presented results of mineralogical experimental and thermodynamic studies indicate that in natural hydrothermal (including uranium-bearing) solutions at temperatures close to 200oC and lower, the formation of the sulfate ion is almost ceased. Sulfide sulfur is oxidized only to S- due to the kinetic peculiarities of the oxidation reactions.
The suggested mechanism of redox reactions of sulfur compounds explains the natural phenomena at the certain stage of the hydrothermal process (200oC and lower) by:
- formation of pseudomorphoses of pitchblende by sulfides;
- deposition of pitchblende in association with disulfides in any rocks in the absence of strong reducing agents;
- a higher content of uranium in ores in regions of development of strong reducing agents, because the buffer action of sulfate sulfur is eliminated;
- formation of ferrous molybdenite;
- deposition of sulfo salts of Ag, As, Sb.
#
Komarov I.A., Melchakova L.V., Ogorodova L.P., Zhuravlev M.I. Experimental thermochemical study of freezing of pore solutions in disperse rocks.key words [pore solution freezing] Moscow State University
Based on a complex analysis of defrosting thermograms, calorimetric studies, and determination of thermophysical parameters of rocks containing Na and K chloride solutions, we discovered a thermal effect that we assigned to the process of cryohydrate formation in disperse rocks [1,2]. Later the existence of this effect was confirmed by NMR studies of the system.
In this work we have carried out a quantitative estimation of cryohydrate formation processes. We used a differential scanning calorimeter (DSC) 'Mettler TA-2000B' in the temperature range from +50 to 100oC, the heating and cooling rates varied from 0.1 to 2-5L/min, the samples (both soils and solutions) were compressed into aluminium crucible, the charges were varied from 30 mg (in small crucibles) to 140mg (in large crucibles). The rocks of disturbed construction, i.e. sands, kaolin, Na-montmorillonite, hydromicaceous clay, containing NaCl and KCl solutions, and, also sea salt and NaCl solutions of various concentrations themselves were studied.
Two endothermal effects were documented on differential thermal curves upon heating NaCl, KCl, and sea salt solutions from 100 to +20oC. The first effect was observed at temperatures close to 0oC, the second one was observed near the eutectic temperature = -21oC for NaCl and 11oC for KCl) (fig.1a).
As the temperature is decreased from 100 to +20oC the solutions get supercooled as a result of which the temperature of the first effect shifts by 10-20oC (freezing point), and that of the second effect by 20-25oC (cryohydrate formation temperature) (fig.1b).
The effect of cryohydrate formation was also observed in wet salinated specimens of sand and kaolin, but it is absent in Na-montmorillonite and hydromicaceous clay (fig.2), which may be related to a strong energy effect of the developed specific surface on a pore solution (S=600m2/g).
The values of freezing heats of salt solutions of various concentrations measured by the DSC vary from 320-330 J/g for small concentrations (5 g/l and 32.3g/l) to 220-250 J/l for strong concentrations (273 g/l) for all the investigated types of salinations.
# This work was supported by the RFBR (Project N. 98-05-64864)
36
Fig.1. DTA curve for NaCl aqueous solution at heating (a) and freezing (b).
Fig.2. Characteristic DTA curves of kaolinite clay in the heating (1) and freezing (2) cycle.
References:
#Komarov I.A., Tol'berg S.A. Thermodynamic model for estimation of freezing temperature and rock moisture composition from sorption isotherms and solubility polytherms.
key words [freezing temeprature moisture in rock] Moscow State University
No unique approach exists presently for the description of various categories of moisture in rocks. There are, however, partly universal models to be proposed.
The principal assumptions used in deriving the formula (1) are as follows: ice that forms in pores liberates and occurs under normal pressure, the freezing rates are such that large ice crystals tend to form in pores, and in salt-rich rocks ice crystals force salt ions out into water films; the values of differential wetting heats, adsorption and dissolution are temperature independent; the energy influence of a specific active surface of rocks and of dissolved ions proceeds in an additive manner; the specific heat of the pore moisture for saltless and salt-containing rocks are taken both for supercooled water and analogous salt solutions in a volume, respectively.
Given that the water state in the liquid phase is chosen as standard, the principal formula for the freezing temperature estimation will be written in the form
 (1)
(1)
where a is the activity;  =To-Tf; Tf is the freezing temperature; To=273.15K; Ta is the rock temperature; L is the phase transition heat; R is the universal gas constant; [Hio-Hi] is the enthalpy difference, taken depending on the equilibrium type, as the differential wetting heat (adsorption, dissolution), the parameters
=To-Tf; Tf is the freezing temperature; To=273.15K; Ta is the rock temperature; L is the phase transition heat; R is the universal gas constant; [Hio-Hi] is the enthalpy difference, taken depending on the equilibrium type, as the differential wetting heat (adsorption, dissolution), the parameters  ,
,  ,
, 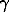 for the adsorption equilibrium are found from specific heat of ice and supercooled water presented as series with respect to temperature, as proposed by Low P.E., Anderson D.M., Hoekstra P., and in the case of chemical equilibrium with respect to specific heat of ice and solutions with account taken of the dependence of specific heat on the concentration and type of salt.
for the adsorption equilibrium are found from specific heat of ice and supercooled water presented as series with respect to temperature, as proposed by Low P.E., Anderson D.M., Hoekstra P., and in the case of chemical equilibrium with respect to specific heat of ice and solutions with account taken of the dependence of specific heat on the concentration and type of salt.
Calculation from the adsorption equilibrium data. The phase equilibrium parameters were found by taking the values of differential heat adsorption and chemical potential from sorption isotherms for kaolinite and Na-montmorrilonite clay at various moistures. Θ was then calculated from (1) and the unfrozen water content (W) vs the temperature curves were plotted (fig.1). The curves were compared with the experimental data for those rocks. A satisfactory agreement was obtained.
Fig.1. Comparison of the experimental values (Wu) for samples of Na-montmorillonite (1) and kaolinite (2) clays with the calculated data.
# This work was supported by the RFBR (Project N. 98-05-64864)
37
Calculation from the solubility polytherms. The freezing temperatures were estimated for sand samples enriched in NaCl and Na2SO4 which have a qualitatively different behaviour depending on the concentration. For the corresponding salts and their molar concentrations the values were found from the reference data: for differential dissolution heats; for solvent activity with account of ionic force.
Using these estimates we then evaluated the freezing temperature using a two-step procedure (at the first step the freezing temperature of sand is estimated at a zero ionic concentration, at the second it is estimated at a current concentration). The comparison of the calculated and experimental data, illustrated in fig.2, has shown their satisfactory agreement.
Fig.2. Comparison of the experimental freezing temperature values (tf), salt-rich Na2SO4 and NaCl with the calculated data.
# Malinin S.D., Kurovskaya N.A.Principal regularities of mineral solubility in chloride fluids under the parameters of homogeneous and heterogeneous states of fluids.
key words [mineral solubility chloride fluid]
Vernadsky Institute of Geochemistry and Analytical Chemistry, RAS 117975 Moscow Kosygin Str., 19
An extremal scantiness and scatter in the available data on mineral solubility in fluids have impelled the authors to conducting systematic studies of mineral solubility in water-chloride solutions under the parameters of the fluid state. Over several years the authors were concerned with experimental studies of the system CaF2(k) NaCl-CaCl2-H2O and CaWO4(k) NaCl- CaCl2- H2O at temperatures 400-800oC, pressures 0.5-2 kbar, with the concentrations of individual chlorides and their mixtures from0.05 to 34.7 mole/kg H2O in the regions of homogeneous and heterogeneous fluid states [1-5].
The solubility studies were carried out by a capsule technique using a weight loss method, the runs were performed in a two-chamber high pressure cell provided with an external heater and a rapid isobaric quenching system.
The results of the studies are reported here.
The following regularities have been established for the homogeneous state of the chloride fluids in question.
1. Solubility of the both minerals grows drastically with the chloride concentration, the dependence being stronger in CaCl2 solution despite the effect of the common calcium ion. Combined with the total high solubility, this fact attests the complex formation in the systems.
2. The dependence of solubility on the chloride concentration in a logarithmic scale is linear in the first approximation. For the solubility of CaF2 in NaCl solutions at 800oC and 2 kbar the linearity is found in the range of NaCl concentrations from 0.2 to 0.35 mole/kg H2O. The slope of the isotherms remains herewith constant within 500-800oC for NaCl and CaCl2 solutions alike.
3. The diagrams of the both systems are close in appearance despite the significantly different chemical nature of the minerals. The isotherms slope stability within 500-800oC gives evidence for the invariability of the composition of dissolved particles in the temperatural range.
4. The solubility data have been used to identify particles of the dissolved mineral substance by a method of fitting on the base of a number of assumptions. The forms (Na2WO4NaCl)o and (CaWO4CaCl2)o have been proposed for the system with scheelite, and (NaFNaCl)o (CaF2CaCl2)o for the system with fluorite. The approach employed does not enable one to solve uniquely the problem of estimation of particular form of particles, but it enables one to estimate the type of particles, in this case neutral in the charge, multiple-mixed in the composition.
The following regularities have been established for the mineral solubility in heterogeneous fluids at 600-800oC and 0.5-2 kbar.
1. At the fluid decomposition in the system with NaCl, as a result of decompression, the mineral solubility changes in a jump-like manner (by approximately one order of magnitude), that is stipulated by the specific feature of mineral solubility in fluids, namely, by the drastic dependence of the solubility on the concentration of NaCl in a fluid. At 800oC the effect of the solubility jump is more pronounced than at 600oC.
2. As the concentration of NaCl is changed, in the heterogeneous region under the isobaric conditions the decompression of the phases and the solubility of fluorite are quantitatively described by the equation of the rule of the gravity center which is manifested in the proportional dependence of solubility on the fraction of the liquid phase in the heterogeneous system and gives evidence for the hydrolytic stability of NaCl solutions. This makes it possible to quantitatively estimate the mineral solubility in different parts of the system both in the heterogeneous and homogeneous regions (near the interphase boundary) based on minimal experimental data.
3. Studies of fluorite solubility in CaCl2 and CaCl2+NaCl solutions at 600oC and 0.5-2 kbar establish no relationship between the supposed phase transition and fluorite solubility which is attributed to deep hydrolysis in these systems.
4. The major criterion of manifestation of the effect of solubility increase under the phase decomposition is the character of the solubility dependence on the salt compo-
# This work was supported by the RFBR (Project N. 97-05-64036)
38
nent concentration in the fluid. The realization of the effect necessitates that the solubility should increase in proportion with the degree of the salt component concentration value higher than unity, the effect being manifested the stronger the higher is the degree.
The obtained results are beyond the scope of particular systems and are suggestive of a general conception of regularities of mineral solubility in supercritical solutions. Based on the general regularities of mineral solubility in fluids, we can propose the following factors for mineral deposition from solutions:
1. Simple cooling of a mineral saturated solution.
2. Isothermal dilution of a saturated solution with water.
3. Combined case dilution of a solution with subsequent cooling.
4. Change in the solution composition: extraction of Ca2+ from a solution (replacement by Na).
Decompression leading to the fluid heterogenization cannot be a deposition factor, as it was commonly believed. On the contrary this process increases the solvent action of a fluid and contributes to stabilization of the dissolved mineral substance.
References:
Petukhov P.A. Thermodynamic contents of models of solid solutions based on experiments on phase equilibrium and their agreement with other data.
Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, 142432 Moscow Region
key words [thermodynamic model solid solution]
The development of thermodynamic models from data on phase equilibria between solid solutions is based on equality of chemical potentials of the components for co-existing phase compositions. Experimental data compare points of compositions for which this equality is fulfilled, and the values of chemical potentials themselves are unknown, only their equality in these points is determined, i.e., the model is based on relative data.
In the general case, this is a quite correct mathematical model that has the thermodynamic form, but values of thermodynamic parameters obtained by the model are expressed in the inherent calculation scale. Of course, this model can be used for studying equilibria of the phase studied (for example, to determine the temperature or pressure of the mineral formation process from the co-existing compositions), but its use for obtaining quantitative values of thermodynamic properties (for example, for calculation of reactions with other phases) is not substantiated.
To develop a model with the quantitative thermodynamic content, one should synthesize a model based on the agreement of data on phase equilibria with those of thermochemical and crystallochemical studies. Efficient agreement requires, first, that the model form would provide a sufficient flexibility and, second, it would assume the direct accordance with the very wide range of studies. In particular, for agreement with data of low-temperature calorimetry, it is desirable that the model form assume a correct extrapolation to the low-temperature region.
In the case of decomposition of a solid solution, the very popular models of solid solutions, which represent thermodynamic functions of mixing in the form of third-power polynomials of the components of the solution composition, relate rigidly data on phase ratios to quantitative values of the excessive energy of mixing of the solid solution. The necessary flexibility of the model can be achieved by the supplement of the polynomials with terms with higher powers. This procedure is described in detail in [1]. The values of excessive enthalpy (He), entropy (Se), and volume (Ve) are usually calculated by these polynomials for the specified composition of the solution, and based on these data, the excessive energy of mixing (Ge) is calculated for the specified temperature (T) and pressure (P):
Ge = He TSe +PVe
Formally, in this expression the excessive enthalpy has a sense of the excessive enthalpy at T = 0 K, and the excessive entropy has a sense of the configuration entropy, but in fact this model works correctly in some specified temperature range and does not assume extrapolation to zero values of temperature; therefore, the formal sense of these parameters is fictitious.
Somewhat different form of the model can be suggested.
Based on the following:
1) the excessive isobaric heat capacity (Cp) approaching T = 0 K tends to zero;
2) the temperature dependence of the excessive heat capacity can have a maximum and allow inversion; we can present the temperature dependence of the excessive heat capacity in the form of a fractional function with two parameters (A, B):
Cp = AT/(e2B +T 2)
and using this function and the configuration entropy (Scon) (in the case of successive agreement of experimental data with the model, this value can be expected to be not fictitious.), we can determine the other excessive thermodynamic parameters:
T T
He = ∫o Cpdt, Se= ∫o Cp/T dt, Ge = He-T(Scon + Se) + PVe
The approaches supposed were successfully approbated for modeling of the three-component solution of feldspars based on the agreement of experimental data of different characters. The B parameter was accepted to be constant, and the A, Scon, and Ve values were determined by the parameters of the fourth-power polynomials on the components of the solution composition by the procedure described in [1].
Reference:
39
#Vigasina M.F., Orlov R.Yu., Shabatina A.V., Dadze T.P. Raman spectroscopy study of antimony complexes in a sulfide-alkaline solution.
key words [antimony complexes solution Raman spectrocopy] Moscow State Unibersity
The problem of transfer of ore components, specifically of gold, has drawn attention to thiocomplexes of antimony. S.A.Wood studied water solutions of thioantimonate by the Raman spectroscopy method (S.A.Wood, 1989) He examined the dissolution of antimonite (Sb2S3) at room temperature in a 1m Na2S water solution, the concentration of Sb being from 0.005 to 0.1 m/l.
We have studied this system at temperatures to 130oC, Sb concentration from 0.005 to 0.1 m/l and Na2S concentrations from 0.1 to 0.8 m/l. The reactants were placed into a microautoclave (0.6 ml in volume) fabricated from a melted quartz or sapphire monoblock. The spectrum was recorded with an optical multichannel analyser.
At every concentration of antimony the spectrum demonstrates at least two RS lines the intensive well polarized 367 cm-1 line and the depolarized 378 cm-1 line. At Na2S concentrations in excess of 0.5 m/l the third 350 cm-1 line is sometimes observed. Besides, pure Na2S solution is characterized by the weak 316 cm-1 line.
S.Wood observed four lines at frequencies 380, 369, 350, and 314 cm-1 which he totally assigned to a vibrational spectrum of a Sb2S4-2 dimer. In doing so he was erroneous in the determination of the degree of depolarization of the 380 cm-1 line and in the assignment of the 314 cm-1 frequency vibrations to the thiocomplex.
Based on those results and his own quantum chemical calculations J.Tossell assigned the 380 cm-1 and 369 cm-1 frequencies to vibrations of H2SbS3- and HSbS3-2 groups, and the 350 cm-1 and 314 cm-1 frequencies to vibrations of a H2Sb2S4 dimer (J.A.Tossell, 1994).
At the same time there are Raman spectra of Na3SbS4 salt and its water solution (W.Mikenda, A.Preisinger, 1980) containing the polarized 367 cm-1 line and the depolarized 380cm-1 line which, most probably, correspond to vibrations of a SbS4-3 group or its protonic forms.
According to our quantum chemical calculation (program GAMESS) the SbS4-3 complex of symmetry Td is characterized by the vibrational frequencies: 139 cm-1 (E), 187cm-1 (F2), 334 cm-1 (A), and 360 cm-1 (F2). So, the frequency of a polarized RS line (type A) ought to be lower than that of a depolarized line (type F2) which, precisely, is observed in experiment. The calculated interatomic distances Sb-S=2.32Å agree with those known for a salt Na3SbS4 (Von H.A.Graf, H.Schafer, 1976). The calculated atomic charges (according to Malliken) equal: Sb=(+1.164); S=(-1.041).
Fig. Raman spectra of thioantimonate-ion in a water Na2S solution: a) S.Wood , [Na2S]=1.0 m/l, [Sb]=0.1m/l; b) the authors, [Na2S]=0.18 m/l, [Sb]=0.05 m/l; p=polarized, dp-depolarized spectral components, s-solvent line.
Conclusions. The Raman spectrum observable at every concentration of Na2S and Sb (367 and 378 cm-1 lines) corresponds to the SbS4-3 complex, and only the irregularly observable 350 cm-1 line is, possibly, related with a more complicated complex. In conclusion it will be recalled that there in nature silver thioantimonate (5) billingsleite Ag7SbS6.
References:
# This work was supported by the RFBR (Project N. 95-05-14560)
40