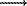 Z (k1)
Z (k1)Genetic petrology and mineralogy
Egorov D.G. Computer modeling of origin of ferruginous quartzites from the Kola Peninsula in terms of the theory of self-organization.
key words [metamorphic differentiation calculation]
Geologic and isotopic - geochemical information, petrochemical mass-balance recalculations and calculations using a method of Gibbs free energy minimization show that ferruginous quartzites from the iron ore formation of the Kola gain-loss were derived from the stress-shear metamorphism of primary highly ferruginous basic vulkanites in situ, the gain-loss of the substance being of inferior significance in scales of the ore-bearing Kola series as a whole.
Metamorphic differentiation is the process restricted in its manifestation by diffusion rates of the components. As shown in a number of the works by V.E.Panin, a combination of stress and shear can lead to the transition of the substance to the atom-vacancy state (AVS) with a drastic increase of the diffusion rates (up to ten orders of magnitude). This promotes the occurrence of the metamorphic differentiation processes at scale levels up to hundreds of meters.
A simplest model of the process in question is as follows: in the zones traversed by a fluid flux iron oxidizes with the formation of magnetite; accordingly, ferrous iron becomes deficient and therefore starts diffusing from the regions surrounding the active zone; the rest of the rock-forming elements, in accord with the mass-balance, are forced out and lost, in doing so aluminium as the most inert element in the metamorphometasomatic process deposits in the direct vicinity of the forming ore bodies and forms alumosilicate gneisses framing ferruginous quartzites lens. The fluid is, herewith, regarded not as a transport agent (the solid-phase process of the substance to the AVS is being assumed) but as an oxidant for ferruginous minerals.
In this case, more intricate synergetic effects associated with a nonlinear interaction of the components in the system are possible. We have performed a numerical modeling of the system describing redistribution of iron with its extraction from ferrosilicate (Fs) and redeposition in the form of magnetite (Mt). We shall designate all the complexes incorporating the block [Fe2+2Fe3+] as X [Fe2+2Fe3+] as Y, Fe2+ as Z, Fe3+ as R.
Given below is the model scheme of the reactions; the kinetic constants of the direct and reverse (if there is such in the scheme) reactions, respectively:
Fs 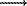 Z (k1)
Z (k1)
Z  R (k2 k3)
R (k2 k3)
Z+R  Y (k4 k5)
Y (k4 k5)
Y+R  (k6 k7)
(k6 k7)
X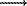 Mt (k8)
Mt (k8)
X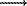 3R (k9)
3R (k9)
Mt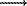 Z+2R (k10)
Z+2R (k10)
Assuming that all the complex formation reactions are equilibrium ones, we shall write the following kinetic equations (for the reactions occurring on the mineral surface the kinetics is proportional to the degree 2/3-the surface-to-volume ratio):
dM/dt = [k8*ZR2 - k10]Mt2/3
dFs/dt= -k1Fs2/3
dZ/dt = k1Fs2/3 – k2Z + k3R k9*ZR2 - [k8*ZR2 - k10]Mt2/3 +
+ Dfe2 Z u(
Z u(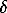 Z/
Z/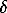 x)
x)
dR/dt = k2Z - k3R + k9*ZR2 - 2[k8*ZR2 - k10]Mt2/3 + Dfe2 R -
R -
- u(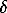 R/
R/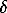 x), where k8* = (k4/k5)(k6/k7)k8; k9* = (k4/k5)(k6/k7)k9.
x), where k8* = (k4/k5)(k6/k7)k8; k9* = (k4/k5)(k6/k7)k9.
The system in question was numerically studied in one- and two-dimensional versions. As the process evolves, the stationary periodic structure of R and Z concentrations forms from the initially homogeneous distribution of all the variables that leads to the wave-like character of distribution of the magnetite being formed.
Galiunin R.V. Axiomatics of geology.
key words [fractal chaos crystal]
The highest level of formalization of every scientific domain is connected with its axiomatic construction. It offers a possibility for further development of science in a purely mathematical way. The gist of the axiomatic method is that out of all reliably established facts several, desirably simplest ones, be distinguished wherefrom the greatest number of the known phenomena should logically follow.
Most processes in geology are reduced to the fact that a discrete component (solid, liquid, gas) chaotically lying in the Earth's crust transits to the liquid state (melt, solution), then this component migrates to subsequently concentrate as a deposit [1]. The discrete component distribution is formalized by the Delaunay systems, i.e., aggregates of points that satisfy two conditions: r- discreteness and R-coverage [2,3]. The first condition does not allow the points to lie too dense, the second to lie too sparse, i.e. the points distribute approximately uniformly in space. Each Delanay system correlates unambiguously with graph whose apices are all the points of the system. The algorithm to construct such a graph is termed Delaunay's triangulation. A mathematical modeling of geologic processes, e.g., magma solidification processes, leads to Delaunay's triangulation [2].
59
Discrete components can move by any of the laws of motion. If the function defining this law is smooth, then according to the theorem of analytical continuation along any as small as one wishes portion of its trajectory, all the trajectory is unambiguously restored. If the law of motion has a fractal character, then, automatically, there appear attractors which may be regarded as the regions of the discrete component concentration (deposits).
Concentrations of such type occur until the components begin to interact with each other, i.e., when the discreteness radius r approximately equalizes with the coverage radius R. The approximation of this process leads only to the ideal crystal, that is, to the formation consisting of equal particles equally surrounded by all the other such particles. Such formations possess Fedorov's symmetry groups. They can arise in all spaces of constant curvature: euclidic, spheric, hyperbolic (Lobachevsky space). Spheric crystals are fullerenes, hyperbolic ones are quasicrystals.
So, naturally, only two extremal practically unattainable stable states of the discrete substance can exist: chaos and ideal crystal [2]. All the states of the discrete substance observable in practice are intermediate between these two. So, the driving force of not only geologic process but of all the processes leading to the substance concentration is crystallization, and the end destiny of the Earth and of the Universe as a whole is to be crystal. From chaos to crystal - such is the gist of evolution. But to be the crystal the Earth has to select such Fedorov group and to arrange all the atoms of the Periodic Table in such positions that each atomic sort should occupy its correct system. To this end, the Earth's life cycle should be approximately 100 billions years with the energy influx received by the Earth presently being retained. There are ideas that the solid part of the Earth's core is crystalline [4] ( the Earth is an autoclave to the solution-melt crystal growth), white dwarfs (stars) are crystals composed of atoms with the lowest stable electrons, neutron stars are crystals composed of nucleons, black holes are quark crystals. It has been found that the gravity centers of 420 supergalaxies discovered by the present time lie lattice-like [5].
If the global transfer of the substance in geological processes has a fractal character, then fractals themselves can be mathematical models of such deposits. In particular Tulia's fractals can serve as 2D mathematical model of the deposits where the motion of the particles which form them follows Mandelbrot's equation. In the case that this motion is sinusoidal, the deposits will have the form of Antonyuk's [6] and Galiulin's [7] fractals. The complexity of the deposit boundaries is characterized by their fractal dimensionality. As a consequence of the scale invariance of fractals one can find rock samples on the deposit boundaries that copy the deposits.
Magmatic, metasomatic, hydrothermal- each of these processes evolves according to its own scenario, but all these processes possess, also, scale invariance, complexity of the boundaries, attractors and repellers, i.e., all the features of fractals. It should be also mentioned that intuitively geologists have long understood the fractality of the processes they are concerned with, for example that intrusives are repellers for gold atoms whereas fractures are attractors, etc.
So, the processes of formation of mineral resources in the Earth's crust can be characterized by two axioms:
1. Chaotically distributed component transits to the fluid-dynamic state;
2. The laws of motion of a component are nonlinear.
All the rest is consequences of these two axioms.
Fig.Galiulin's fractal.
References:
60