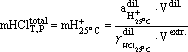The solubility of baddeleyite (ZrO2) and zircon (ZrSiO4)

Solubility of baddeleyite (ZrO₂) and zircon (ZrSiO₄)
in aqueous hydrochloric solutions at elevated T and P parameters
Korzhinskaya V.S.^#

Institute of Experimental Mineralogy
Russian Academy of Sciences 142432 Chernogolovka Moscow distr., Russia

^{#The work has been sponsored by the RFBR (Grant N 97-05-65826, 99-05-64106, Grant of the leading research schools 96-16-98333)

Information on the stability of zirconium compounds is very important for understanding geochemical behaviour of such minerals as baddeleyite and zircon in hydrothermal processes. It is still to be answered why zircon is uncommon to hydrothermal conditions of formation of rare metal and other deposits which are accompanied by considerable wall rock alterations. As is known, zircon is found only in rocks associated with alkaline metasomatism. The problem can be tackled through experimental studies on solubility of zircon and baddeleyite, on the dependence of their stability on temperature, pressure, pH and composition of the active solution under hydrothermal conditions.
Presently, the information on the behaviour of zirconium in solutions at elevated T-P parameters is scarce, and the available data obtained for water solutions pertain to normal conditions. Due to high charge, small radius and comparatively small ionisation potential zirconium ions in a solution tend to hydrolysis and complexing with anions of organic and inorganic acids. Therefore, because of complexity and peculiarity of chemical behaviour of zirconium compounds in water solutions the problem of forms of existence of ions in them has not been conclusively solved [36-37].
According to Nazarenko et. al.(1979) and Savin et. al.(1974) [26, 33] such hydrocomplexes of zirconium as Zr⁺⁴, Zr(OH)⁺³, Zr(OH)₂⁺², Zr(OH)₃⁺, Zr(OH)₄ exist, depending on pH, in a solution under normal conditions. The system ZrO₂-HNO₃-H₂O was studied by Sazhina et. al., (1982) at T=25^oC in the range of nitric acid concentration 10.8-53.7 wt % and 26.3-9.18 wt % ZrO₂ [31]. It was shown that under those conditions the concentration of zirconium in a nitric acid solution decreased with growing acid concentration. A minimum solubility value was in the range of 45-50 wt pct. HNO₃.
Karlysheva et. al.(1982 ) [13] studied zirconium complexing with CO₃-ions . They investigated the interaction of zirconium oxychloride (ZrOCl₂) with Na₂CO₃ in water solutions using IR spectroscopy and pH-metry to find that a Zr(OH)₂(CO₃)₂^-2 complex forms at pH=7. The complex decomposed with decreasing pH to form Zr(OH)₄ at pH=1.8. At greater length the complexing of zirconium in hydrocarbonate solutions was studied by Samchuk and Dorofey (1983 ) [32] for the system Zr(OH)₄-HCO₃-H₂O at 25^oC. The authors showed that the presence of hydrocarbonate-ions increased the solubility of Zr(OH)₄ by 2-3 orders of magnitude as compared with water. It was concluded that hydrobicarbonate complexes were one of the forms of zirconium migration in natural waters.
The problem of the influence of physicochemical mineral formation conditions on the deposition of zircon and baddeleyite in ore bodies has not, however, been solved because some thermodynamic constants of these two minerals and of zirconium particles in a hydrothermal fluid are unknown or unreliable. Therefore, direct experimental studies of mineral solubility at elevated T-P parameters are of primary importance.
In this report we give the results of a study of baddeleyite and zircon solubility in a supercritical HCl fluid in a broad range of temperatures and concentrations.
Methods and experimental techniques
Solubility studies of zirconium minerals were performed by capsule and buffer techniques.
Solubility of baddeleyite in a HCl fluid was studied by a capsule technique with a further analysis of the composition of quenched solution and solid phase in a hydrothermal high pressure apparatus [12]. The experimental temperatures ranged from 400 to 600^oC, pressures from 1 to 2 kbar, muriatic acid concentrations from 10^-2 to 4 mole/kg H₂O. The measurement accuracy was not lower than +5^oC for the temperature and +25 bar for the pressure. The runs were conducted in platinum tubes (10x0.2x50 mm) whereinto a mineral charge (30mg) was placed. Both chemical reagent ZrO₂ (high purity grade) in the form of crystalline substance (crystal sizes 15-30 μm) and synthetic baddeleyite grown by us under hydrothermal conditions at T=400-500^oC and P=1 kbar from ZrCl₄ were used as the mineral charge. Muriatic acid solutions of preset concentration were prepared from ficsanal? by diluting them with bidistilled water. HCl concentrated solutions were prepared from HCl conc. (high purity grade).
The runs concerned with the effect of salt loading (NaCl) on the solubility of baddeleyite were carried out at T=500^oC, P=1 kbar and HCl concentrations: 0.01; 0.1, and 1 mole/kg H₂O. The concentration of NaCl was 0.1; 0.5; 1 and 2 mole/ kg H₂O. The amount of the solution in capsules was constant ( 1ml ).
The charged capsule was sealed and held under static conditions at chosen T-P. After quenching the capsule was opened and its contents was washed out with distilled water, acidified with HCl, into a test tube. The solution was then separated from the mineral charge with the aid of a filter. Zirconium in the solution was determined photocalorimetrically at an apparatus SPECOL using an arsenazo III indicator [1]. Inasmuch as an equilibrium concentration of zirconium in the solution was always much lower than the concentration of hydrochloric acid, the values of the latter after the run were taken to be equal to its values before the run. The composition of solid products were examined in a polarizing microscope and by X-ray diffraction. Always, after the run , baddeleyite was the only solid phase.

9
Baddeleyite reached an equilibrium after 5-14 days which was found by special runs of different durations for T=400, 50, 600^oC, P=1 kbar, and 1m HCl. As seen from the diagram in fig.1, for 400^oC in the beginning, in the first 2-4 days, the concentration of zirconium in the fluid becomes greater that the equilibrium value, and it gradually decreases down to the equilibrium value in the course of 10-14 days. This phenomenon is observed in studies of other minerals, from example in the works of Korzhinskiy (1987), Kudrin (1985) [17, 19]. It can be attributed to different rates of the direct and reverse reactions of dissolution and precipitation.
We studied the solubility of zircon in the system ZrO₂-SiO₂-H₂O-HCl in the temperature range 400-600^oC, at P=1 kbar and HCl concentrations from 1.8 to 0.02 mole/kg H₂O using a buffer technique enabling the maintenance of HÑl^o constant activity at given T and P conditions [6]. The buffer was a solid Ag-AgCl mixture in combination with various redox buffer (Ni-NiO; Co-CoO; Fe₃O₄-Fe₂O₃). In our runs we used a modified method enabling us to approach an equilibrium from two sides [15]. Fig.2 represents schematically the charging of capsules. The procedure was as follows: four platinum capsules measuring 3x0.1x50 mm and 4^.0.1^.40 mm were located in the same working volume of constant T, P, and chemical potential of hydrogen. Two of the capsules (3 mm) acted as fixing agents of HCl^o activity and contained a solid buffering mixture Ag-AgCl and a H₂O-HCl solution of various initial concentrations. The two other capsules (4 mm) contained the same Ag-AgCl buffer, zircon-quartz association and ZrCl₄^aq of various initial concentrations. The hermetically sealed platinum capsules were located in a large gold capsule (10x0.2x50 mm) together with an oxygen solid buffer. There into a required amount of distilled water was filled after which the gold capsule was hermetically sealed and placed into a hydrothermal vessel to perform a run at the given T and P parameters until an equilibrium was reached. The duration of the runs varied from 10 days for 600^oC to 30 days for 400^oC [3, 8, 16]. Such a procedure made it possible to control simultaneously in all the four platinum capsules the hydrogen fugacity and, accordingly, an equilibrium concentration of HCl^o, an in the capsules, containing the zircon + quartz charge, an equilibrium concentration of Zr^aq at the given T,P parameters. The equilibrium in the system was considered to be reached when the concentration of HCl^o in the two platinum capsules, containing only the Ag-AgCl buffer, differed by no greater than +0.06 log.un., and the concentrations of zirconium in the fluid in the other two capsules differed by no greater than +0.07 log.un. mZr^aq. After the run the concentration of HCl was defined from the pH value of the quenched solution taken from the capsules containing only the Ag-AgCl buffer. To that purpose 0.1 ml quenched solution was taken with a calibrated pipet (0.1 + 0.0005 ml) and diluted with bidistilled water (1 ml). The measured pH value was recalculated using the following equilibrium:

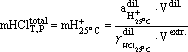(1)
were V^dil., a_H⁺_25^oC^dil., g
_HCl25^oC^dil., are the volume, the hydrogen ion activity, and the coefficient of HCl activity, respectively, pertinent to the diluted solution [2]; V^extr. is the volume of the extracted quenched solution. The concentration of zirconium in the solution from the other two capsules was measured photocalorimetrically with arsenazo III.

Fig.1. Charging of capsules, schematic. 1 - sealed gold capsules; 2-3 - platinum capsules with buffers Ag-AgCl+H₂O and Ag-AgCl+HCl+H₂O; 4-5 - platinum capsules with buffers Ag-AgCl + Zrc+Q+H₂O and Ag-AgCl+Zrc+Q+ZrCl₄aq; 6 - MOx-MOy (redox couple) buffer.

Fig.2. Results of kinetic runs in the system ZrO₂-H₂O-HCl at T=400-600^oC and P=1 kbar (m_HCl=1 mole/kg H₂O)

10
Table 1. Conditions and results of the baddeleyite solubility study in the system ZrO₂-H₂O-HCl ( capsule technique)

Sample number
m_HCl mole/kg H₂O
lgmHCl
aH⁺
+γ
-lgK_dHCl^o
mHCl^o mole/kg H₂O
-lgmHCl^o
-lgmZraq

T=400^oC P=1kbar t=14d V_H2O=1.443

1
0.01
2.000
5.91E-03
0.7946
-1.867
2.57E-03
2.590
4.074

2
0.1
1.000
4.38E-02
0.6298

5.62E-02
1.251
4.012

3
0.2
0.699
4.17E-02
0.5783

0.128
0.893
3.885

4
0.4
0.398
6.20E-02
0.5285

0.283
0.549
4.068

5
0.65
0.187
8.12E-02
0.4953

0.486
0.313
4.022

6
0.8
9.69E-02
9.11E-02
0.4817

0.611
0.214
3.975

7
1.0
0
0.1029
0.4675

0.780
0.108
3.683

8
2.0
-0.301
0.1496
0.4263

1.649
-0.217
2.157

9
4.0
-0.602
0.2163
0.3901

3.446
-0.537
0.969

10
H₂0

4.890

T=400^oC P=2kbar t=14d V_H2O=1.261

1
0.01
2.000
7.64E-03
0.8172
-1.052
6.54E-04
3.183
3.990

2
0.1
1.000
4.77E-02
0.6416

2.56E-02
1.591
4.050

3
0.2
0.699
7.77E-02
0.5880

6.79E-02
1.168
3.955

4
0.4
0.398
0.1233
0.5386

0.171
0.767
4.420

5
0.65
0.187
0.1682
0.5072

0.318
0.497
3.830

6
0.8
9.69E-02
0.1915
0.4947

0.413
0.384
3.720

7
1.0
0
0.2198
0.4819

0.544
0.265
3.728

8
2.0
-0.301
0.3335
0.4460

1.252
-0.098
2.030

9
4.0
-0.602
0.4987
0.4161

2.801
-0.447
0.811

T=500^oC P=1kbar t=7d V_H2O=1.892

1
0.01
2.000
7.18E-04
0.8765
4.251
9.18E-03
2.037
4.712

2
0.1
1.000
2.33E-03
0.7877

9.70E-02
1.013
4.583

3
0.2
0.699
3.31E-03
0.7524

0.196
0.709
4.542

4
0.4
0.398
4.70E-03
0.7125

0.393
0.405
4.375

5
0.65
0.187
6.00E-03
0.6819

0.641
0.193
4.710

6
0.8
9.69E-02
6.70E-03
0.6681

0.790
0.102
4.171

7
1.0
0
7.40E-03
0.6529

0.988
0.005
4.112

8
2.0
-0.301
1.06E-02
0.6030

1.982
-0.297
3.855

9
4.0
-0.602
1.49E-02
0.5496

3.973
-0.599
2.759

10
H20

5.430

T=500^oC P=2kbar t=7d V_H2O=1.446

1
0.01
2.000
3.70E-03
0.8319
2.624
5.61E-03
2.251
4.618

2
0.1
1.000
1.38E-02
0.7089

8.10E-02
1.094
4.631

3
0.2
0.699
2.01E-02
0.6661

0.170
0.770
4.420

4
0.4
0.398
2.90E-02
0.6215

0.353
0.452
4.367

5
0.65
0.187
3.73E-02
0.5897

0.587
0.232
4.657

6
0.8
9.69E-02
4.16E-02
0.5760

0.728
0.138
3.955

7
1.0
0
4.67E-02
0.5614

0.917
0.038
4.061

8
2.0
-0.301
6.67E-02
0.5167

1.871
-0.272
2.822

9
4.0
-0.602
9.50E-02
0.4739

3.799
-0.580
1.953

T=600^oC P=1kbar t=7d V_H2O=2.673

1
0.01
2.000
3.48E-05
0.9531
6.915
9.96E-03
2.002
4.656

2
0.1
1.000
1.10E-04
0.9173

9.99E-02
1.001
4.486

3
0.2
0.699
1.56E-04
0.9021

0.200
0.699
4.502

4
0.4
0.398
2.20E-04
0.8842

0.400
0.398
4.520

5
0.65
0.187
2.81E-04
0.8699

0.650
0.187
4.395

6
0.8
0.097
3.12E-04
0.8632

0.800
0.097
4.310

7
1.0
0
3.49E-04
0.8557

0.99996
0
4.301

8
2.0
-0.301
4.93E-04
0.8298

1.9994
-0.301
4.063

9
4.0
-0.602
6.97E-04
0.7997

3.9991
-0.602
2.968

10
H₂0

5.050

T=600^oC P=2kbar t=7d V_H2O=1.694

1
0.01
2.000
7.97E-04
0.8927
4.156
9.11E-03
2.041
4.881

2
0.1
1.000
2.60E-03
0.8154

9.68E-02
1.014
4.827

3
0.2
0.699
3.69E-03
0.7847

0.195
0.709
4.799

4
0.4
0.398
5.24E-03
0.7500

0.393
0.406
4.739

5
0.65
0.187
6.69E-03
0.7232

0.641
0.193
4.604

6
0.8
0.097
7.43E-03
0.7112

0.789
0.103
4.517

7
1.0
0
8.31E-03
0.6979

0.988
5.21E-03
4.357

8
2.0
-0.301
1.18E-02
0.6542

1.982
-0.297
3.162

9
4.0
-0.602
1.67E-02
0.6071

3.973
-0.599
2.321

11
The zircon-quartz association is a mixture of zircon and quartz minerals (40 mg). We used synthetic quartz furnace-preheated to 900^oC and cooled in cold distilled water. The monolith cracked to pieces which were ground to powder (30 μm particles) in an agate mortar. Synthetic ZrSiO₄ of tetragonal syngony with the grain size of 10-15 μm, produced by us under hydrothermal conditions, was used as the mineral zircon [11].

Results and discussion
Solubility of baddeleyite. The experimental results on the baddeleyite solubility in the system ZrO₂-H₂O-HCl are given in table 1. The bulk concentrations of HCl in the fluid after the run were recalculated with respect to the concentration of the associated HCl^o using the data on the dissociation constants of hydrochloric acid, borrowed from the work by Frantz and Marshall (1984) [7]. The activity coefficients for ionic particles were calculated from the second-order Debye-Huckel equation [10].
Figs. 3a,3b gives the logarithmic dependence between the concentration of the associated HCl^o and the concentration of zirconium in equilibrium with baddeleyite for temperatures 400, 500, and 600^oC and pressure P = 1kbar (fig.3a) and 2 kbar (fig.3b). All the isotherms demonstrate the same picture, namely, their slopes do not remain constant as the concentration of hydrochloric acid grows. In water and in the region of low HCl concentrations (HCl concentration Ð
0.2 m ) the solubility of baddeleyite is, practically, independent of the HCl^o concentration. The dominant equilibrium in this region, like in water, is believed to be as follows:
ZrO₂ + 2H₂O = Zr(OH)_4^o (2)
with the equilibrium constant
K_p = mZr(OH)_4^o (3)
The solubility of baddeleyite is insignificant in this region and, as seen from table 1, makes up: for 400^o - 1.28^.10^-5, for 500^o - 3.72^.10^-6, and for 600^oC 8.90^.10^-6 mole/kg H₂O.
The general principles of experimental data treatment aimed at identification of particles, formed in the solution, involve the comparison of theoretically expected slopes of solubility isotherms as a function of chlorides concentration from a number of hypothetic reactions of mineral dissolution with experimentally established slopes, and a further selection of reactions in accordance with the criterion of best fit of the theoretical and experimental slopes. In this scheme it is supposed that associated neutral particles dominate in the solution because the study was carried out at high temperatures and using high concentrations of hydrochloric acid. Based on this method and using the information Mwakio (1985), Nazarenko et.al.(1979) [23, 26], on the state of zirconium ions in water solutions at 25^o and 80^oC , one can suppose that at T=400-600^oC and P=1 kbar Zr(OH)_4^o, Zr(OH)₃Cl^o, Zr(OH)₂Cl_2^o, Zr(OH)Cl_3^o, and ZrCl_4^o were dominant particles in the solution.
In the range of hydrochloric acid concentrations 0,2-0,8 mole/kg H₂O the slope of isotherms which reflect the relationship between the associated HCl^o and Zr_aq , dissolved in the fluid, is not constant. This may be associated with a change of zirconium complexes in the solution simultaneously. The following equilibria can exist, theoretically, in this region
ZrO₂ + HCl^o = Zr(OH)₃Cl^o (4)
ZrO₂ + 2HCl^o = Zr(OH)₂Cl_2^o (5)
ZrO₂ + 3HCl^o = Zr(OH)Cl_3^o (6)
Their equilibrium constants have the form:
K_p = mZr(OH)₃Cl^o/mHCl^o (7)
K_p = mZr(OH)₂Cl_2^o/m²HCl^o (8)
K_p = mZr(OH)Cl_3^o/m³HCl^o (9)
In the region of concentrated hydrochloric solution (mHCl³
0,8 mole/kg H₂O) the solubility of baddeleyite drastically increases by 2-4 orders of magnitude. In this region (dlog mZr_aq/dlog mHCl)=4 and the dominant equilibrium in this region will be the following one
ZrO₂ + 4HCl^o = ZrCl_4^o + 2H₂O (10)
with the equilibrium constant:
K_p = mZrCl_4^o/m⁴HCl^o (11)
Table 2 giver the calculated values of the equilibrium constants (2,4,5,6,10).
Comparison of the baddeleyite solubility data obtained at different temperatures and constant pressure and hydrochloric acid concentration shows that the concentration of zirconium in the solution decreases with growing temperature. For example, at P=2 kbar for the diluted region (m_HCl=0,01 m) the solubility of baddeleyite is 8.91^.10^-5 at 400^o; 2.34^.10^-5 at 500^o, and 1.49^.10^-5 at 600^oC. In the concentrated region (m_HCl=4 m) the concentration of zirconium in the solution is 1.55^.10^-1 at 400^o; 1.11^.10^-2 at 500^o; and 1.78^.10^-3 at 600^oC. It should be mentioned that such a behavior is observable for other chloride salts as well in studies of hydrolysis reactions [8,9,28].

12

Table 2. Equilibrium constants of the reactions, controlling the baddeleyite solubility

Reaction
-lgK_p

400^o
500^o
600^o

ZrO₂ + 2H₂O =Zr(OH)₄^o
4.89+0.120
5.43+0.025
5.05+0.14

ZrO₂ + HCl^o + H₂O = Zr(OH)₃Cl^o
3.60+0.021
4.16+0.070
4.30+0.061

ZrO₂ + 2HCl^o =Zr(OH)₂Cl₂^o
3.48+0.033
4.40+0.042
4.61+0.045

ZrO₂ + 3HCl^o =Zr(OH)Cl₃^o
3.39+0.012
4.76+0.019
5.00+0.031

ZrO₂ + 4HCl^o =ZrCl₄^o+ H₂O
3.32+0.017
5.16+0.025
5.48+0.030

However, as seen from fig.3a, at P=1 kbar, this dependence in the diluted region of HCl concentrations is different, and an equilibrium concentration of zirconium is higher at T=600^oC than at T=500^oC. At m_HCl = 0.01 m the concentration of zirconium in the solution is 1.94^.10^-5 at 500^oC and 2.21^.10^-5 mole/kg H₂O at 600^oC. A pressure growth from 1 to 2 kbar, temperature and HCl concentration being constant, leads to an increase of mZr^aq. The role of pressure is, however, less significant.

Fig.3. (a,b) - Solubility of baddeleyite in HCl solutions at T=400-600^oC.
Table 3. Conditions and results of the baddeleyite solubility study in the system ZrO₂-H₂O-HCl (technique involving a Ag-AgCl buffer)

Initial solution
pH
-lgmHCl total
mHCl^o mol/kg H₂O
-lgmHCl^o
-lgmZr^aq
-lgH⁺
+γ
aH⁺

T=500^oC P=1kbar t=15d V_H2O=1.892 Co-CoO-Ag-AgCl-H₂O-HCl

H₂O
1.34
0.08
0.8215
0.0854
-
1.991
0.6655
6.79E-03

1.5mHCl
1.33
0.09
0.8028
0.0954
-
1.997
0.6671
6.71E-03

H2O
-
-

3.990

0.1mZrCl₄
-
-

4.069

T=500^oC P=1kbar t=15d V_H2O=1.892 Ni-NiO-Ag-AgO-H₂O-HCl

H₂O
1.61
0.33
0.4552
0.3418
-
2.143
0.7036
5.06E-03

1mHCl
1.60
0.34
0.4499
0.3468
-
2.147
0.7043
5.03E-03

H₂O
-
-

4.362

0.1mZrCl₄

4.296

In fig.3a (shaded squares) and table 3 are given the data on the solubility of baddeleyite at T=500^oC and 1 kbar obtained with the use of Ag-AgCl buffer in combination with oxygen buffers Co-CoO and Ni-NiO. As seen from fig.3a the solubility values of baddeleyite obtained by the capsule technique and by using buffer are in good agreement, the differences do not exceed 0.05 log un.

13

Fig.4 illustrates the results of three series of runs on baddeleyite solubility in mixed HCl+NaCl solutions at T=500^oC and P=1 kbar. As seen from the diagram, with the initial HCl concentration of 0,1 and 0,01m the concentration of zirconium in the solution is lower throughout than in the absence of electrolyte. This may be attributed to partial dissociation of hydroxochloride complexes of zirconium due to addition into the solution of extra chlorine ion that decreases an equilibrium zirconium concentration. At mHCl=1 mole/kg H₂O the adding of NaCl increases the solubility of baddeleyite that is attributed to the formation of undissociated complex of zirconium with sodium. Analogous results were obtained in cassiterite solubility studies at the same T and P parameters in HCl+NaCl solutions performed by Kovalenko et. al. (1986) [18].

Fig.4. Solubility of baddeleyite in HCl+NaCl solutions at T=500^oC and P=1 kbar.
Fig.5. Solubility of zircon in a water solution of HCl at 400, 500, 600^oC and P=1 kbar in the presence of quartz.

Fig.6. Concentrations of zirconium and silicon in a solution in equilibrium with baddeleyite-zircon and zircon-quartz associations at T=600^oC, P=1 kbar, mHCl=1 mole/kg H₂O. 1 - experimental data; 2 – calculations from thermodynamic data.
Fig.7. Alterations of the amount of equilibrium SiO₂aq in a solution vs the temperature for a baddeleyite-zircon association.
Solubility of zircon. Incongruent solubility of zircon with the formation of quartz can be represented in the form of equilibrium:
ZrSiO₄+ xHCl^o_aq= SiO₂ + Zr(OH)_4-nCl_n^oaq + (x-2) H₂O

Zrc Q (12)
The equilibrium constant of this reaction is as follows:
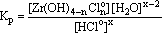(13)
Under the assumption that the behavior of uncharged particles in the fluid is ideal and the activity of water is close to unity, this constant can be written as
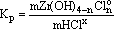(14)
where m is the molality (mole/kg H₂O). As suggested by the equilibrium (14), the solubility of zircon depends solely on the activity of associated HCl in the solution at given T,P conditions. By analogy with the baddeleyite solubility study, the gross HCl concentration values were recalculated with respect to the concentration of undissociated HCl^o, and zirconium dissolved in the fluid phase was in the associated forms.

14

The initial conditions and the experimental results are given in table 4. Fig.5 shows the relationship between the concentration of zirconium in hydrothermal solution and the concentration of associated HCl^o in equilibrium with the zircon-quartz association at different temperatures and P=1 kbar. As seen from the diagram, the equilibrium concentrations of zirconium in the fluid with the constant HCl^o concentration decrease with temperature. All the three isotherms have the same slope, i.e., the ratio (d log mZr_aq/d log mHCl) =1. One can assume that under these conditions Zr(OH)₃Cl^o is the dominant complex for which an equilibrium is written as
ZrSiO₄ + HCl^o + H₂O = Zr(OH)₃Cl^o + SiO₂solid (15)
Table 4. Conditions and results of the zircon solubility study in the system ZrO₂-SiO₂-H₂O-HCl (P=1 kbar)

Sample name
T, ^oC
During
Initial solution
pH in diluted solution
Equilibrium values of -lgm_HCl
Equilibrium values of -lgm_{Zr aq}
-lgmHCl^o
+γ
aH⁺
lgK

Co-CoO-Ag-AgCl-H₂O-HCl

Zr-33(1)
400
30
H₂O
1.91
0.33
-
0.472
0.5176
6.76E-02
1.505

Zr-33(2)
400
30
1.5 m HCl
1.97
0.37
-
0.517
0.5240
6.42E-02

Zr-33(3)
400
30
0.1 m ZrCl₄
-
-
1.98
-
-
-

Zr-33(4)
400
30
H₂O
-
-
2.02
-
-
-

Zr-51(1)
500
14
H₂O
1.30
0.12
-
0.126
0.6717
6.48E-02
2.255

Zr-51(2)
500
14
1.5 m HCl
1.38
0.11
-
0.116
0.6701
6.56E-02

Zr-51(3)
500
14
H₂O
-
-
2.40
-
-
-

Zr-51(4)
500
14
0.1 m ZrCl₄
-
-
2.36
-
-
-

Zr-147(1)
600
12
H₂O
1.96
-0.27
-
-0.269
0.8327
4.76E-03
2.590

Zr-147(2)
600
12
2m HCl
1.98
-0/23
-
-0.229
0.8363
4.54E-03

Zr-147(3)
600
12
H₂O
-
-
2.31
-
-
-

Zr-147(4)
600
12
0.1 m ZrCl₄
-
-
2.37
-
-
-

Ni-NiO-Ag-AgCl-H₂O-HCl

Zr-24(1)
400
30
H₂O
1.78
0.60
-
0.7785
0.5616
4.75E-02
1.495

Zr-24(2)
400
30
1 m HCl
1.74
0.54
-
0.7097
0.5517
5.14E-02

Zr-24(3)
400
30
H₂O
-
-
2.26
-
-
-

Zr-24(4)
400
30
0.1 m ZrCl₄
-
-
2.22
-
-
-

Zr-50(1)
500
14
H₂O
1.68
0.38
-
0.3871
0.7100
4.80E-03
2.270

Zr-50(2)
500
14
1 m HCl
1.67
0.37
-
0.3770
0.7086
4.85E-03

Zr-50(3)
500
14
H₂O
-
-
2.63
-
-
-

Zr-50(4)
500
14
0.1 m ZrCl₄
-
-
2.68
-
-
-

Zr-150(1)
600
14
H₂O
1.60
0.18
-
0.1802
0.8694
2.83E-04
2.555

Zr-150(2)
600
14
2m HCl
1.61
0.16
-
0.1602
0.8679
2.89E-04

Zr-150(3)
600
14
H₂O
-
-
2.70
-
-
-

Zr-150(4)
600
14
0.1 m ZrCl₄
-
-
2.75
-
-
-

Fe₃O₄- Fe₂O₃-Ag-AgCl-H₂O-HCl

Zr-143(1)
400
30
H₂O
2.80
1.38
-
1.2773
0.6949
1.59E-02
1.300

Zr-143 (2)
400
30
2 m HCl
2.94
1.39
-
1.7403
0.6966
1.57E-02

Zr-143 (3)
400
30
H₂O
-
-
3.03
-
-
-

Zr-143 (4)
400
30
0.1 m ZrCl₄
-
-
3.-4
-
-
-

Zr-141 (1)
500
18
H₂O
2.57
1.13
-
1.1449
0.8017
2.01E-03
2.245

Zr-141 (2)
500
18
2 m HCl
2.60
1.20
-
1.2160
0.8088
1.85E-03

Zr-141 (3)
500
18
H₂O
-
-
3.39
-
-
-

Zr-141 (4)
500
18
0.1 m ZrCl₄
-
-
3.46
-
-
-

Zr-140 (1)
600
14
H₂O
2.54
1.03
-
1.0305
0.9187
1.06E-04
2.570

Zr-140 (2)
600
14
1m HCl
2.52
1.02
-
1.0205
0.9183
1.07E-04

Zr-140 (3)
600
14
H₂O
-
-
3.57
-
-
-

Zr-140 (4)
600
14
0.1 m ZrCl₄
-
-
3.62
-
-
-

It has to be mentioned that at T=400^oC in the range of low HCl concentrations ( in the presence of a hematite-magnetite buffer) the slope of the curve is not 45^o. It can be assumed that under these conditions along with Zr(OH)₃Cl^o there are other zirconium chloride complexes in the solution.
Comparison of the solubility data for zircon and baddeleyite at the same T-P-mHCl conditions has shown that the concentration of zirconium in the solution in equilibrium with a zircon-quartz association is by 1-1.5 order of magnitude higher against an equilibrium with baddeleyite. This is in contradiction with thermodynamic data since the activity of zirconium in dioxide has to be higher than in salt. To understand this phenomenon we carried out additional runs with baddeleyite-zircon and zircon-quartz associations at T=400-600^oC, P=1 kbar in H₂O-HCl solutions ( in the absence of an Ag-AgCl buffer) using the capsule technique. After the run the quenched solutions were

15

analysed for the concentration of H₄SiO₄. The results are listed in table 5. Fig.6 gives the data reflecting the equilibrium concentrations of zirconium in the solution with baddeleyite-zircon and zircon-quartz associations at T=600^oC, P=1 kbar, and mHCl=1M. The data were obtained by different techniques. Three fields are distinguished on the diagram, corresponding to: I stability of baddeleyite; II stability of zircon; III stability of zircon-quartz association. The stability field of baddeleyite is separated from the field of zircon with the line corresponding to the equilibrium:
ZrO₂ + H₄SiO_4^o = ZrSiO₄ + 2H₂O (16)
The fields of zircon and zircon-quartz association are separated with the line, corresponding to the solubility of quartz. It has been found that a baddeleyite-zircon equilibrium is reached at log mH₄SiO_4^o = (-2.41 ¸
-2.47), herewith log mZr_aq = -4.20¸
-4.40. According to the data of McKenzie and Helgeson (1984 )[22], the concentration of SiO_2aq in equilibrium with quartz for the given T-P parameters is 1.35 log un. In this case in the system H₂O-HCl (without Ag-AgCl buffer) the experimentally defined concentration of zirconium in the solution in equilibrium with zircon-quartz association is 5.32 log un., but it is 2.78 log un. in the presence of the Ag-AgCl buffer. Fig.6 gives, also, the theoretical values of zirconium concentration in the solution, calculated from the thermodynamic equilibrium data (15). The calculation procedure was as follows.
The thermodynamic data for zircon were corrected from equilibrium (16), using the experimental data on the concentration of silicon in the solution in equilibrium with zircon and baddeleyite.
Free Gibbs energies of a Zr(OH)₃Cl^o particle were calculated from our experimental data on baddeleyite solubility according to equilibrium (4) (see above).
Concentrations of zirconium in the solution in equilibrium with zircon-quartz association were calculated in accordance with eq.(15). The thermodynamic data for minerals and particles, used in the calculations, are listed in tables 6 and 7.
Comparison of the calculated and experimental (without Ag-AgCl buffer) data on zirconium concentration in the solution shows a fair agreement. The difference is no greater than 0.1 log.un. But where the Ag-AgCl buffer technique is employed the value for the same association is log mZr_aq=- 2.78. The difference may be due to the formation of complicated heteropolynuclear complexes of zirconium with silicon in the presence of silver which acts as a catalyst and, probably, stabilizes these complexes. The analogous picture of formation of heteropolynuclear tin-silicon complexes was observed in solubility studies of SnO₂ [27]. It has to be mentioned that when baddeleyite solubility was studied with the Ag-AgCl buffer technique, in the absence of quartz in the system, no increase of zirconium concentration in the solution was observed.
The values of free Gibbs energy for zircon and baddeleyite were reconciled from equilibrium (16) using our experimental data on the concentration of silicon in the solution in equilibrium with baddeleyite-zircon association and on the concentration of zirconium in the solution in equilibrium with zircon-quartz association. The thermodynamic data for baddeleyite were borrowed from the work by Kelley (1960) [14], and for a H₄SiO₄ particle from the work by Walther and Helgeson (1977) [38], listed in table 7. The diagram of fig.7 gives in the coordinates T-logmH₄SiO₄ the concentrations of equilibrium H₄SiO_4aq, calculated from the thermodynamic data of various authors and our experimental data for the temperature range of 400-600^oC at P=1 kbar. As suggested by an analysis of the diagram, our experimental data on equilibrium concentrations of H₄SiO_4^o agree best with the calculated values obtained using thermodynamics for zircon and baddeleyite by Schuiling (1976), Matveev et. al.(1983) [34, 21]. The differences are no greater than 0,15 log un., which corresponds to 0.5-0.6 kcal/mole for the free Gibbs energy of zircon.
The obtained experimental data combined with the thermodynamic properties of the complexes enable more rigorous estimations of forms of zirconium transport in natural waters. Based on the existing ideas of the parameters of hydrothermal mineral formation , one can admit that temperatures 400-600^oC at which we conducted runs on zircon and baddeleyite solubility are allowable both for acidic and alkaline metasomatites. The pressure P=1 kbar corresponds to optimal pressure for these formations but there are, indeed, higher and lower pressures. As for the composition of the acted hydrothermal solution, it is somewhat different for acidic and alkaline metasomatites.
According to the data on gas-liquid inclusions, the temperature range of acidic metasomatites (involving such formations as greisens, represented by quartz and muscovite; secondary quartzites, represented by quartz and andalusite, quartz and pyrophillite; quartz-feldspathic metasomatites, represented by quartz, orthoclase and hematite) spans 300 - 550^oC, and the concentration of chlorides in a fluid can reach 20-40 wt pct which corresponds to their molar fraction of 0.1 - 0.2 [24]. For alkaline metasomatites ( including such formations as albitites, represented by albite, chlorite, algirite, riebeckite and others) the composition of the acted solution is characterized by lower chloride concentration and by the presence of hydrocarbonate-chloride-sodium component [20]. A distinctive feature of the process of acidic metasomatoses is the regime of increased chlorinity of the acted solution. According to the experimental data of Poop and Frantz(1980) [29] the concentration of hydrochloric acid in the hydrothermal process at the stage of acidic metasomatosis cannot exceed 10^-3 – 10^-2 mole/ kg H₂O even at very high chloride concentrations.
So, based on our experimental data we can conclude that a significant increase of solubility of baddeleyite and zircon (see above) is observed only in HCl solutions with the concentration mHCl 0,8 mole/kg H₂O, and prior to this concentration the content of zirconium in the solution is approximately 10^-5 mole/kg H₂O. As seen from the analysis, such high concentrations of HCl are absolutely unreal for hydrothermal postmagmatic processes, therefore transport of zirconium in the form of hydroxochloride complexes of zirconium is quite improbable at the stage of acidic metasomatosis. This is also supported by retrograde solubility of zircon and baddeleyite in a fluid in the temperature range 400 - 600^oC and by a weak influence of additional saline loading in the form of NaCl on an equilibrium concentration of zirconium in a solution.

16

Table 5. Conditions and results of experimental study on baddeleyite-zircon and zircon-quartz associations in hydrothermal solution at P=1 kbar

Initial solution
Final solution

Charge, mg
T, ^oC
During t, days
mHCl mole/
kgH₂O
-lgmHCl^o
-lgmSiO₂ ^aq
-lgmZr ^aq
lgK
Phase composi-
tion

ZrO₂
ZrSiO₄
SiO₂

16.4
-
6.0
600
12
1mHCl
0.119
-
4.783

Zrc+Bd
Zrc+Bd+Q
Zrc+Bd+Q
Zrc+Bd+Q
Zrc+Bd+Q
Zrc+Bd+Q
Zrc+Bd+Q
Zrc+Bd
Zrc+Bd
Zrc+Bd

16.4
-
8.0
600
12
1mHCl
0.119
-
4.741

16.4
-
8.5
600
12
1mHCl
0.119
1.962
3.857

16.4
-
9.0
600
12
1mHCl
0.119
1.660
3.898

16.4
-
9.5
600
12
1mHCl
0.119
1.484
4.302

16.4
-
10.0
600
12
1mHCl
0.119
1.359
4.662

16.4
-
14.0
600
12
1mHCl
0.119
-
4.862

20.0
20.0
-
600
10
0.01mHCl
2.07
2.468
4.608
2.47

20.0
20.0
-
600
10
0.01mHCl
2.07
2.414
4.835
2.41

20.0
20.0
-
600
10
1mHCl
0.119
-
4.586

-
20.0
20.0
600
10
1mHCl
0.119
-
5.32
-5.20
Zrc+Q
Zrc+Bd
Zrc+Bd
Zrc+Bd
Zrc+Bd

20.0
20.0
-
400
24
0.01mHCl
2.59
3.272
-
3.27

20.0
20.0
-
400
24
0.01mHCl
2.59
3.324
-

3.32

20.0
20.0
-
500
12
0.01mHCl
2.11
2.760
-
2.76
20.0
20.0
-
500
12
0.01mHCl
2.11
2.703
-
2.70

Table 6. Available thermodynamic data for ZrO₂ and ZrSiO₄

-ΔH^o₂₉₈ kcal/mol
-ΔG^o₂₉₈ kcal/mole
S^o₂₉₈cal/(mole Grad)
C^o₂₉₈ cal/(mol. Grad)
a
b
c
T, interval (K)
Refe-
rence

ZrO₂

-
-
-
13.39
16.64
1.80
-3.36
298-1478
[4]
263.04
249.27
12.12
13.40
16.64
1.80
-3.36
298-1478
[23]

262.978
-
12.04
13.37
68.329
9.081
-13.438
298-1445
[32]

262.3
248.505
12.04
13.41
90.70
4.388
-8.133
298-1478
[27]

ZrSiO₄

-
459.02
-
-
-
-
-
-
[31]
-
-
-
23.55
31.48
3.92
8.08
298-1800
[4]
488.050
460.325
-
-
-
-
-
1300-1400
[20]
485.994
458.626
20.08
13.41
-
-
-
-
[27]
484.0
456.684
20.2
12.56
31.48
3.92
8.08
298-1800
[14]
475.7
448.4
20.2
12.56
31.48
3.92
8.08
298-1800
[23]
486.138
458.891
20.086
-
-
-
-
-
[32]

Table 7. Free Gibbs energies of formation of minerals and particles in a solution(P=1kbar).

Mineral
Formula
mol.volume cal/bar
-ΔG_f^o kcal/mol
Reference

400^oC
500^oC
600^oC

Bd
ZrO₂
0.5055
232.177
227.699
223.251
[14]

Zrc
ZrSiO₄
0.9383
426.944
417.709
408.886
Authors data

Q
SiO₂
0.5423
188.334
184.047
179.808
[35]

Zr(OH)₄^o

304.407
288.429
276.856
Authors data

Zr(OH)₃Cl^o

283.560
271.431
259.492
Authors data

Zr(OH)₂Cl₂^o

259.560
248.113
237.316
Authors data

Zr(OH)Cl₃^o

235.548
225.042
214.620
Authors data

ZrCl₄^o

211.291
201.618
191.605
Authors data

H₄SiO₄^o

268.653
257.782
247.075
[35]

HCl^o

18.719
17.661
15.727
[7]

H₂O

42.807
39.571
36.435
[5]

Conclusions. The principal results obtained on solubility of baddeleyite in a HCl fluid under high T-P conditions are the following:
Solubility of baddeleyite in pure water and diluted solutions of hydrochloric acid is insignificant and is, practically, independent on the concentration of HCl to 0,2 m. The dominant complex in this concentration region of HCl is Zr(OH)_4^o. In the concentration region of HCl higher than 0,2 m the solubility of baddeleyite increases drastically and the dominant complexes are mixed hydroxochloride complexes of zirconium of the type Zr(OH)_4-nCl_n^o, where 'n' varies from 0 to 4. The dominant complex in the concentrated region (mHCl 0.8 m) is ZrCl_4^o.
The solubility of baddeleyite at a constant concentration of HCl decreases with temperature. The effect of pressure on the solubility of baddeleyite is insignificant.
The principal results obtained on the solubility of zircon in the presence of quartz are the following:
The concentration of zirconium in a solution in equilibrium with a zircon-quartz association in the presence of a Ag-AgCl buffer is higher than in equilibrium with baddeleyite under the same T-P and mHCl conditions. This is due to the formation of heteropolynuclear complexes of zirconium with silicon in the presence of silver.

17

The concentration of zirconium in a solution in equilibrium with a zircon-quartz association decreases with temperature.
The values of free Gibbs energies are refined for zircon by using the experimental data on the concentration of H₄SiO_4^o in a solution in equilibrium with a zircon-quartz association.
The transport of zirconium and its deposition at the hydrothermal mineral formation stage occurs in solutions of increased alkalinihy with the participation of hydrocarbonate chloride-sodium solutions. The occurrence of sodium ions, hydrocarbonate anions in the acted solution at the stage of alkaline metasomatosis is responsible for clear rare-metal mineralization.
References:

Busev A.I., Tiptsova V.G., Ivanov V.M. (1978) Manual on analytical Chemistry of Rare Elements. // . M., Khimiya, pp.161-162 (In Rus.)

Chemist`s Guide Ed. B.P.Nicolskii (1964.) // M- L:Khimiya, v.3,1005 p.(In Rus.)

Chou I-M., Eugster H.P. (1977) Solubility of Mt in supercritical chloride solution - Amer.J.Sci., v.277, N10, pp.1067-1072.

Coughlin J.P., King E.G. (1950) High-temperature heat contents of some zirconium containing substances. // J. Amer. Chem. Soc., v.72, p.2262.

Fischer J.R., Zen E.A. (1971) Thermochemical calculations from hydrothermal phase equilibrium data and the free energy of H₂O // Amer. J. Sci., v.270, p.p.297-314.

Frantz J.D., Eugster H.P. (1973) Acid-base buffers: use of Ag-AgCl in the experimental control of solution equilibria at elevated pressures and temperatures // Amer. J. Sci.,, v.273, N3, pp.268-286.

Frantz J.D., Marshall W.L. (1984) Electrical conductances and ionization constants of salt, acids and bases in supercritical aqueous fluids: I.Hydrochloric acid from 100-700^oC and at pressures to 4000 bars // Amer. J. Sci., v.284, pp.651-667.

Frantz J.D., Popp R.K. (1979) Mineral-solution equilibria.I.An experimental study of completing and thermodynamic properties of aqueous MgCl₂ in the system MgO-SiO₂-H₂O-HCl - Geochim. et Cosmochim. Acta, v.43, N8, pp.1223-1239.

Gunter W.D., Eugster H.P. (1978) Wollastonite solubility and free energy of supercritical aqueous CaCl₂ // Contrib.Mineral. Petrol.,v.66, N3, p.p.1777-1790.

Helgeson H.C., Kirkham D.H., Flowers T.C. (1981) Theoretical prediction of thermodynamic behavior of aqueous electrolytes at high pressures and temperatures. IV.Calculation of activity coefficients, osmotic coefficients apparent molal and standart relative partial molal properties to 600^oC and 5 kbar // Amer. J. Sci., v.281, N10, p.p.1249-1516.

Ivanov I.P., Korzhinskaya V.S. (1983) Method for synthesis of zirconium silicate Auth.cert.N1021109, USSR. (In Rus.)

Ivanov I.P., Likhoidov G.G., Plusnina L.P., Chernyshova G.N., Ryzhkov S.M., Dmitrenko L.T. (1979) Modernized hydrothermal apparatus for an investigation of mineral equilibria // Geochimiya, , N11, p.1668. (In Rus.)

Karlysheva K.F., Chumakova L.S., Malinko L.A., Sheka I.A. (1982) Interaction of zirconium and hafnium oxichlorides with sodium carbonate In a solution // Russian Journal of Inorganic Chemistry, v.27, N11, p.2793.(In Rus.)

Kelley K.K. (1960) Contributions to the data on theoretical metallurgy.XIII. High-temperature heat contents, heat capacity and entropy data for the elements and inorganic compounds // U.S. Bur. Miner.Bull., v.584, p.232.

Korzhinskaya V.S., Ivanov I.P. (1988) Experimental study of incongruent solubility of zircon in the system ZrO₂-SiO₂-H₂O-HCl at T=400-600^oC and P=1 kbar // Doklady Acad. Nauk USSR, v.299, N4, pp.970-973.

Korzhinskiy M.A. (1981) Investigation of a Ag-AgCl buffer in the region of low m
H₂ values //Outline of phys.-chem. Petrology, M., Nauka, pp.41-51. (In rus.)

Korzhinskiy M.A. (1987) The solubility of corundum in an HCl fluid and forms taken by Al. // Geochemistry International, v.24, N11, pp.105-109.

Kovalenko N.I., Ryzhenko B.N., Barsukov V.L., Klintsova A.P.,Velyukhanova T.K., Volynets M.P. and Kitayeva L.P. (1986) The solubility of cassiterite in HCl and HCl+NaCl(KCl) solutions at 500^oC and 1000 atm under fixed redox conditions. //Geochemistry International, v.23, N7, pp.66-78.

Kudrin A.V. (1985) The solubility of tugarinovite MoO₂ in aqueous solutions at elevated temperatures. // Geochemistry International, v.22, N9, pp.126-137.

Makarova T.I.,Sidorov Ju.I.,Naumov V.B. (1984) Formation conditions for ferruginous minerals in uranium-bearing alkali metasomatites // Geochim.,N1,, pp.70-83. (In rus.)

Matveev G.M., Zhuravlev A.K., Yudina T.V. (1983) Thermodynamic properties of zircomium silicate crystals at elevated temperatures // Izv. Acad. Nauk SSR, series "Inorganic materials", v.19, N1, p.163.

McKenzie W.F., Helgeson H.C. (1984) Estimation of the dielectric constant of H₂O from experimental solubilities of quartz and calculation of the thermodynamic properties of aqueous species to 900^oC at 2 kbar // Geochim. Cosmochim. Acta, v.48, pp.2167-2177.

Mwakio P.T. (1985) The kinetics of dissolution of zircon (ZrSiO₄) // Geochim. Cosmochim. Acta, v.49, N2, pp.453-458.

Naumov V.B., Naumov G.B. (1980) Mineralizing fluids and physicochemical regularities of their evolution // Geochim.,N10, pp.1450-1460. (In rus.)

Naumov G.B., Ryzhenko B.N., Khodakovskii I.L. (1971) Thermodynamic values manual. // M., Atomisdat, p.239.

Nazarenko V.A., Antonovich V.P., Nevskaya E.M. (1979) Hydrolysis of metal ions in diluted solutions //. M., Atomisdat, , pp.101-103. (In rus.)

Nekrasov I.Ja. (1976) Phase ratio in tin-bearing system. // M., Nauka, pp.44-48.

Popp R.K., Frantz J.D. (1979) Mineral solution equilibria. II.An experimental study of mineral solubilities and the thermodynamic properties of aqueous CaCl₂ in the system CaO-SiO₂-H₂O-HCl. // Geochim. Cosmochim. Acta, v.43, N11, pp.1777-1790.

Popp R.K., Frantz J.D. (1980) Mineral solution equilibria-III. The system Na₂O-Al₂O₃-SiO₂-H₂O-HCl // Geochim. Cosmochim. Acta, v.44,N7, pp.1029-1037.

Robie R.A., Hemingwau B.S., Fisher J.R. (1978) Thermodynamic properties of minerals and related substances at 298.15K (25^oC) and 1 bar (10^.5 pascals) // Geol. surv., Bull., Wash., N1259, p.456.

Sazhina V.A., Kolenkova M.A., Saf`yanova N.A., Popova A.I. (1982) On solid phases in the system ZrO₂-HNO₃-H₂O // ZhNKh, v.27, N1, pp.223-226.

Samchuk A.I., Dorofey E.N. (1983) Complexing of zirconium in hydrocarbonate solutions. // Geochim., N8, p.p.236-244.(In rus.)-

Savvin S.B., Dedkova V.P., Dzhashi D.O. et al. (1974) Investigation of the composition and structure of complexes in the system fluoride-zirconium-arsenazoIII // Zh AKh, v.34, N2, pp.300-307.

Schuiling R.D., Vergouwen L., Rijst H. (1976) Gibbs energies of zircon formation (ZrSiO₄), thorite (ThSiO₄) and phenacite(Be₂SiO₄) // Amer. Min., v.62, N1-2, pp.166-168.

Thermodynamic properties of individual substances (1981) Manual. // M., Nauka, book 1,2,4, v.2,3, pp.237,110.(In rus.).

Vasil`ev V.P., Lytkin A.I. (1976) Standard enthalpy of zirconium(IV) ion formation in a water solution // Zh NKh, , N10, p.2610.(In rus.)

Vasil`ev V.P., Kochergina L.A., Lytkin A.I. (1974) Standard isobaric potential of Zr⁺⁴ ion formation in a water solution. //Zh NKh, , N19, pp.2998-2999.

Walther J.V., Helgeson H.C. (1977) Calculation of the thermodynamic properties of aqueous silica and the solubility of quartz and its polymorph at high pressures and temperatures. // Amer. J. Sci., v.277, pp. 1315-1351.

18

Preface
Contents
Next}

Sample number	m_HCl mole/kg H₂O	lgmHCl	aH⁺	+γ	-lgK_dHCl^o	mHCl^o mole/kg H₂O	-lgmHCl^o	-lgmZraq
T=400^oC P=1kbar t=14d V_H2O=1.443
1	0.01	2.000	5.91E-03	0.7946	-1.867	2.57E-03	2.590	4.074
2	0.1	1.000	4.38E-02	0.6298		5.62E-02	1.251	4.012
3	0.2	0.699	4.17E-02	0.5783		0.128	0.893	3.885
4	0.4	0.398	6.20E-02	0.5285		0.283	0.549	4.068
5	0.65	0.187	8.12E-02	0.4953		0.486	0.313	4.022
6	0.8	9.69E-02	9.11E-02	0.4817		0.611	0.214	3.975
7	1.0	0	0.1029	0.4675		0.780	0.108	3.683
8	2.0	-0.301	0.1496	0.4263		1.649	-0.217	2.157
9	4.0	-0.602	0.2163	0.3901		3.446	-0.537	0.969
10	H₂0							4.890
T=400^oC P=2kbar t=14d V_H2O=1.261
1	0.01	2.000	7.64E-03	0.8172	-1.052	6.54E-04	3.183	3.990
2	0.1	1.000	4.77E-02	0.6416		2.56E-02	1.591	4.050
3	0.2	0.699	7.77E-02	0.5880		6.79E-02	1.168	3.955
4	0.4	0.398	0.1233	0.5386		0.171	0.767	4.420
5	0.65	0.187	0.1682	0.5072		0.318	0.497	3.830
6	0.8	9.69E-02	0.1915	0.4947		0.413	0.384	3.720
7	1.0	0	0.2198	0.4819		0.544	0.265	3.728
8	2.0	-0.301	0.3335	0.4460		1.252	-0.098	2.030
9	4.0	-0.602	0.4987	0.4161		2.801	-0.447	0.811
T=500^oC P=1kbar t=7d V_H2O=1.892
1	0.01	2.000	7.18E-04	0.8765	4.251	9.18E-03	2.037	4.712
2	0.1	1.000	2.33E-03	0.7877		9.70E-02	1.013	4.583
3	0.2	0.699	3.31E-03	0.7524		0.196	0.709	4.542
4	0.4	0.398	4.70E-03	0.7125		0.393	0.405	4.375
5	0.65	0.187	6.00E-03	0.6819		0.641	0.193	4.710
6	0.8	9.69E-02	6.70E-03	0.6681		0.790	0.102	4.171
7	1.0	0	7.40E-03	0.6529		0.988	0.005	4.112
8	2.0	-0.301	1.06E-02	0.6030		1.982	-0.297	3.855
9	4.0	-0.602	1.49E-02	0.5496		3.973	-0.599	2.759
10	H20							5.430
T=500^oC P=2kbar t=7d V_H2O=1.446
1	0.01	2.000	3.70E-03	0.8319	2.624	5.61E-03	2.251	4.618
2	0.1	1.000	1.38E-02	0.7089		8.10E-02	1.094	4.631
3	0.2	0.699	2.01E-02	0.6661		0.170	0.770	4.420
4	0.4	0.398	2.90E-02	0.6215		0.353	0.452	4.367
5	0.65	0.187	3.73E-02	0.5897		0.587	0.232	4.657
6	0.8	9.69E-02	4.16E-02	0.5760		0.728	0.138	3.955
7	1.0	0	4.67E-02	0.5614		0.917	0.038	4.061
8	2.0	-0.301	6.67E-02	0.5167		1.871	-0.272	2.822
9	4.0	-0.602	9.50E-02	0.4739		3.799	-0.580	1.953
T=600^oC P=1kbar t=7d V_H2O=2.673
1	0.01	2.000	3.48E-05	0.9531	6.915	9.96E-03	2.002	4.656
2	0.1	1.000	1.10E-04	0.9173		9.99E-02	1.001	4.486
3	0.2	0.699	1.56E-04	0.9021		0.200	0.699	4.502
4	0.4	0.398	2.20E-04	0.8842		0.400	0.398	4.520
5	0.65	0.187	2.81E-04	0.8699		0.650	0.187	4.395
6	0.8	0.097	3.12E-04	0.8632		0.800	0.097	4.310
7	1.0	0	3.49E-04	0.8557		0.99996	0	4.301
8	2.0	-0.301	4.93E-04	0.8298		1.9994	-0.301	4.063
9	4.0	-0.602	6.97E-04	0.7997		3.9991	-0.602	2.968
10	H₂0							5.050
T=600^oC P=2kbar t=7d V_H2O=1.694
1	0.01	2.000	7.97E-04	0.8927	4.156	9.11E-03	2.041	4.881
2	0.1	1.000	2.60E-03	0.8154		9.68E-02	1.014	4.827
3	0.2	0.699	3.69E-03	0.7847		0.195	0.709	4.799
4	0.4	0.398	5.24E-03	0.7500		0.393	0.406	4.739
5	0.65	0.187	6.69E-03	0.7232		0.641	0.193	4.604
6	0.8	0.097	7.43E-03	0.7112		0.789	0.103	4.517
7	1.0	0	8.31E-03	0.6979		0.988	5.21E-03	4.357
8	2.0	-0.301	1.18E-02	0.6542		1.982	-0.297	3.162
9	4.0	-0.602	1.67E-02	0.6071		3.973	-0.599	2.321

Reaction	-lgK_p
Reaction	400^o	500^o	600^o
ZrO₂ + 2H₂O =Zr(OH)₄^o	4.89+0.120	5.43+0.025	5.05+0.14
ZrO₂ + HCl^o + H₂O = Zr(OH)₃Cl^o	3.60+0.021	4.16+0.070	4.30+0.061
ZrO₂ + 2HCl^o =Zr(OH)₂Cl₂^o	3.48+0.033	4.40+0.042	4.61+0.045
ZrO₂ + 3HCl^o =Zr(OH)Cl₃^o	3.39+0.012	4.76+0.019	5.00+0.031
ZrO₂ + 4HCl^o =ZrCl₄^o+ H₂O	3.32+0.017	5.16+0.025	5.48+0.030

H₂O	1.34	0.08	0.8215	0.0854	-	1.991	0.6655	6.79E-03
1.5mHCl	1.33	0.09	0.8028	0.0954	-	1.997	0.6671	6.71E-03
H2O	-	-			3.990
0.1mZrCl₄	-	-			4.069

H₂O	1.61	0.33	0.4552	0.3418	-	2.143	0.7036	5.06E-03
1mHCl	1.60	0.34	0.4499	0.3468	-	2.147	0.7043	5.03E-03
H₂O	-	-			4.362
0.1mZrCl₄				4.296

Sample name	T, ^oC	During	Initial solution	pH in diluted solution	Equilibrium values of -lgm_HCl	Equilibrium values of -lgm_{Zr aq}	-lgmHCl^o	+γ	aH⁺	lgK
Co-CoO-Ag-AgCl-H₂O-HCl
Zr-33(1)	400	30	H₂O	1.91	0.33	-	0.472	0.5176	6.76E-02	1.505
Zr-33(2)	400	30	1.5 m HCl	1.97	0.37	-	0.517	0.5240	6.42E-02
Zr-33(3)	400	30	0.1 m ZrCl₄	-	-	1.98	-	-	-
Zr-33(4)	400	30	H₂O	-	-	2.02	-	-	-
Zr-51(1)	500	14	H₂O	1.30	0.12	-	0.126	0.6717	6.48E-02	2.255
Zr-51(2)	500	14	1.5 m HCl	1.38	0.11	-	0.116	0.6701	6.56E-02
Zr-51(3)	500	14	H₂O	-	-	2.40	-	-	-
Zr-51(4)	500	14	0.1 m ZrCl₄	-	-	2.36	-	-	-
Zr-147(1)	600	12	H₂O	1.96	-0.27	-	-0.269	0.8327	4.76E-03	2.590
Zr-147(2)	600	12	2m HCl	1.98	-0/23	-	-0.229	0.8363	4.54E-03
Zr-147(3)	600	12	H₂O	-	-	2.31	-	-	-
Zr-147(4)	600	12	0.1 m ZrCl₄	-	-	2.37	-	-	-
Ni-NiO-Ag-AgCl-H₂O-HCl
Zr-24(1)	400	30	H₂O	1.78	0.60	-	0.7785	0.5616	4.75E-02	1.495
Zr-24(2)	400	30	1 m HCl	1.74	0.54	-	0.7097	0.5517	5.14E-02
Zr-24(3)	400	30	H₂O	-	-	2.26	-	-	-
Zr-24(4)	400	30	0.1 m ZrCl₄	-	-	2.22	-	-	-
Zr-50(1)	500	14	H₂O	1.68	0.38	-	0.3871	0.7100	4.80E-03	2.270
Zr-50(2)	500	14	1 m HCl	1.67	0.37	-	0.3770	0.7086	4.85E-03
Zr-50(3)	500	14	H₂O	-	-	2.63	-	-	-
Zr-50(4)	500	14	0.1 m ZrCl₄	-	-	2.68	-	-	-
Zr-150(1)	600	14	H₂O	1.60	0.18	-	0.1802	0.8694	2.83E-04	2.555
Zr-150(2)	600	14	2m HCl	1.61	0.16	-	0.1602	0.8679	2.89E-04
Zr-150(3)	600	14	H₂O	-	-	2.70	-	-	-
Zr-150(4)	600	14	0.1 m ZrCl₄	-	-	2.75	-	-	-
Fe₃O₄- Fe₂O₃-Ag-AgCl-H₂O-HCl
Zr-143(1)	400	30	H₂O	2.80	1.38	-	1.2773	0.6949	1.59E-02	1.300
Zr-143 (2)	400	30	2 m HCl	2.94	1.39	-	1.7403	0.6966	1.57E-02
Zr-143 (3)	400	30	H₂O	-	-	3.03	-	-	-
Zr-143 (4)	400	30	0.1 m ZrCl₄	-	-	3.-4	-	-	-
Zr-141 (1)	500	18	H₂O	2.57	1.13	-	1.1449	0.8017	2.01E-03	2.245
Zr-141 (2)	500	18	2 m HCl	2.60	1.20	-	1.2160	0.8088	1.85E-03
Zr-141 (3)	500	18	H₂O	-	-	3.39	-	-	-
Zr-141 (4)	500	18	0.1 m ZrCl₄	-	-	3.46	-	-	-
Zr-140 (1)	600	14	H₂O	2.54	1.03	-	1.0305	0.9187	1.06E-04	2.570
Zr-140 (2)	600	14	1m HCl	2.52	1.02	-	1.0205	0.9183	1.07E-04
Zr-140 (3)	600	14	H₂O	-	-	3.57	-	-	-
Zr-140 (4)	600	14	0.1 m ZrCl₄	-	-	3.62	-	-	-

Initial solution								Final solution
Charge, mg			T, ^oC	During t, days	mHCl mole/ kgH₂O	-lgmHCl^o	-lgmSiO₂ ^aq	-lgmZr ^aq	lgK	Phase composi- tion
ZrO₂	ZrSiO₄	SiO₂	T, ^oC	During t, days	mHCl mole/ kgH₂O	-lgmHCl^o	-lgmSiO₂ ^aq	-lgmZr ^aq	lgK	Phase composi- tion
16.4	-	6.0	600	12	1mHCl	0.119	-	4.783		Zrc+Bd Zrc+Bd+Q Zrc+Bd+Q Zrc+Bd+Q Zrc+Bd+Q Zrc+Bd+Q Zrc+Bd+Q Zrc+Bd Zrc+Bd Zrc+Bd
16.4	-	8.0	600	12	1mHCl	0.119	-	4.741
16.4	-	8.5	600	12	1mHCl	0.119	1.962	3.857
16.4	-	9.0	600	12	1mHCl	0.119	1.660	3.898
16.4	-	9.5	600	12	1mHCl	0.119	1.484	4.302
16.4	-	10.0	600	12	1mHCl	0.119	1.359	4.662
16.4	-	14.0	600	12	1mHCl	0.119	-	4.862
20.0	20.0	-	600	10	0.01mHCl	2.07	2.468	4.608	2.47
20.0	20.0	-	600	10	0.01mHCl	2.07	2.414	4.835	2.41
20.0	20.0	-	600	10	1mHCl	0.119	-	4.586
-	20.0	20.0	600	10	1mHCl	0.119	-	5.32	-5.20	Zrc+Q Zrc+Bd Zrc+Bd Zrc+Bd Zrc+Bd
20.0	20.0	-	400	24	0.01mHCl	2.59	3.272	-	3.27
20.0	20.0	-	400	24	0.01mHCl	2.59	3.324	-	3.32
20.0	20.0	-	500	12	0.01mHCl	2.11	2.760	-	2.76
20.0	20.0	-	500	12	0.01mHCl	2.11	2.703	-	2.70

-ΔH^o₂₉₈ kcal/mol	-ΔG^o₂₉₈ kcal/mole	S^o₂₉₈cal/(mole Grad)	C^o₂₉₈ cal/(mol. Grad)	a	b	c	T, interval (K)	Refe- rence
ZrO₂	-ΔG^o₂₉₈ kcal/mole	S^o₂₉₈cal/(mole Grad)	C^o₂₉₈ cal/(mol. Grad)	a	b	c	T, interval (K)	Refe- rence
-	-	-	13.39	16.64	1.80	-3.36	298-1478	[4]
263.04	249.27	12.12	13.40	16.64	1.80	-3.36	298-1478	[23]
262.978	-	12.04	13.37	68.329	9.081	-13.438	298-1445	[32]
262.3	248.505	12.04	13.41	90.70	4.388	-8.133	298-1478	[27]

-	459.02	-	-	-	-	-	-	[31]
-	-	-	23.55	31.48	3.92	8.08	298-1800	[4]
488.050	460.325	-	-	-	-	-	1300-1400	[20]
485.994	458.626	20.08	13.41	-	-	-	-	[27]
484.0	456.684	20.2	12.56	31.48	3.92	8.08	298-1800	[14]
475.7	448.4	20.2	12.56	31.48	3.92	8.08	298-1800	[23]
486.138	458.891	20.086	-	-	-	-	-	[32]

Mineral	Formula	mol.volume cal/bar	-ΔG_f^o kcal/mol			Reference
Mineral	Formula	mol.volume cal/bar	400^oC	500^oC	600^oC	Reference
Bd	ZrO₂	0.5055	232.177	227.699	223.251	[14]
Zrc	ZrSiO₄	0.9383	426.944	417.709	408.886	Authors data
Q	SiO₂	0.5423	188.334	184.047	179.808	[35]
	Zr(OH)₄^o		304.407	288.429	276.856	Authors data
	Zr(OH)₃Cl^o		283.560	271.431	259.492	Authors data
	Zr(OH)₂Cl₂^o		259.560	248.113	237.316	Authors data
	Zr(OH)Cl₃^o		235.548	225.042	214.620	Authors data
	ZrCl₄^o		211.291	201.618	191.605	Authors data
	H₄SiO₄^o		268.653	257.782	247.075	[35]
	HCl^o		18.719	17.661	15.727	[7]
	H₂O		42.807	39.571	36.435	[5]