 -quartz from supercritical aqueous fluids. // J. of Crystal Growth. N162, pp.142-146.
-quartz from supercritical aqueous fluids. // J. of Crystal Growth. N162, pp.142-146.Crystal growth, structure and physical properties of crystals
#Balitsky V.S., Iwasaki H., Iwasaki F., Bublikova T.M., Mar'ina E.A. and Balitskaya L.V. Experimental and computer simulation of morphology of quartz crystals in connection with conditions of their growth.
key words [quartz morphology synthesis]*Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, Moscow Region, Russia ;**Sobudai-Danchi, 1-6-15-12, Sagamichara 228, Japan;***Moscow State University, Moscow, Russia
Experimental and computer simulation of the morphology of quartz crystals was performed in connection with conditions of their growth. The formation of crystals was experimentally studied in the temperature range from 250 to 900oC and pressure range from 0.3 to 5 kbar under isothermal and thermogradient conditions. Pure water and aqueous solution of NaCl, NaOH, NH4F, HF, and others with the concentration of 0.001--5 wt.% were used as solutions. Amorphous silica (chemically pure grade) was the starting material in isothermal experiments. Quartz or amorphous silica served as the blend in experiments carried out under thermogradient conditions. Experiments were carried out in heat-resistant autoclaves (T to 800oC and P to 1.6 kbar) and hydrothermal and gas high-pressure installations designed in IEM RAS [1]. The computer simulation of the morphology of quartz crystals was performed by the previously developed program [2, 3] on the basis of the fact that the main forming facets are the facets of the main rhombohedra {0111} and {1011} and hexagonal prism {1010} for a-quartz and bipyramid {1011} and hexagonal prism {1010} for b-quartz. The complex studies allowed us to establish specific conditions determining changes in the ratios of the growth rates of the forming facets and to arrange the corresponding rows of changes in the crystal morphology. We confirmed equalizing of the growth rates of the main forming facets as the thermobaric parameters of the process increase, which has been previously observed for natural quartz crystals. At the same time, we showed that the composition, density, and oversaturation of the solution also have a substantial effect on the change in the ratio of the growth rates of facets and appearance of new forming facets. This probably explains nonconformity (often observed in natural quartz) of the real morphology of the crystals to commonly accepted concepts on its relation only to thermobaric crystallization conditions.
References :
 -quartz from supercritical aqueous fluids. // J. of Crystal Growth. N162, pp.142-146.
-quartz from supercritical aqueous fluids. // J. of Crystal Growth. N162, pp.142-146.#Balitsky V.S., Makhina I.B., Mar'in A.A. and Dorogovin B.A. Growth and structural morphological parameters of ametrine - bicolored amethyst-citrine quartz.
key words [ametrine quartz synthesis]
# This works is supported by the Russian Foundation for Basic Research (project N 97-05-64805).
66
*Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, Moscow Region, Russia **All-Russian Research Institute of Synthesis of Mineral Raw Materials, Aleksandrov, Vladimir Region, Russia
The influence of physicochemical and growth factors on capture and distribution of an iron admixture in quartz crystals was experimentally studied. Based on this study, problems of crystallogenesis of all iron-containing varieties of quartz, including bicolored ametrine, were solved. It was established that the main background for the formation of Fe-containing varieties of quartz is determined by Eh-pH of mineral-forming solutions. Amethyst, citrine, and ametrine are formed in the region of the predominant existence of trivalent iron in a solution; green quartz, in the presence of bivalent iron; and brown quartz, near the curve of equilibrium of bi-trivalent iron. At the same time, the formation and stability of various iron-containing centers of color are affected by the temperature, pressure, concentration of an admixture in a solution, crystallographic direction of growth and growth rate of faces, and their orientation during growth. The effect of all the factors mentioned was considered in detail. The first in the world industrial technology of ametrine crystal growth was developed on the basis of the revealed regularities. Similarly to crystals of synthetic amethyst and citrine, ametrine is grown in strongly alkaline potassium solutions in the presence of trivalent iron ions and an oxidant at 350-390oC and 1,3-1,5 kbar. Up to 250-300 kg crystals can be grown in a 1000-l autoclave for the 2-3-month cycle. The weight of single crystals ranges from several grams to 3.5 kg. The crystals can be flattened, prismatic, or isometrical symmetrical and asymmetrical depending on the crystallographic orientation of seeds, its shape and sizes, and duration of growth. They are characterized by the zone-sectorial structure, which is pronounced due to the selective distribution of amethyst and citrine colors in different sectors and zones of growth. The crystals grown on seedings parallel to pinacoid {0001} are characterized by the simplest color distribution. Stones prepared from these crystals can be relatively simply identified on the basis of specific features of their internal structure, color distribution, and IR spectroscopy data. However, in addition to this, the technology developed makes it possible to grow ametrine crystals with morphology and color distribution close to natural crystals. Identification of faceted stones obtained from similar crystals are more complicated and not always unambiguous.
#Kotel'nikov A.R., Koval'skii A.M. and Ogorodova L.P. Solid solutions of (Sr,Ba)-feldspars.
key words [Sr, Ba-feldspar synthesis]
*Institute of Experimental Mineralogy, Russian Academy of Sciences, Chernogolovka, 142432 Moscow Region **Department of Geology, Moscow State University, Vorob'evy Gory, 119899 Moscow,
Binary solid solutions of (Sr,Ba)-feldspars were synthesized by the dry synthesis method and hydrothermal recrystallization. It is shown that at 700-1400oC, these feldspars form continuous solid solutions. The compositions of the feldspars synthesized correspond to stoichiometry of minerals of the (Sr,Ba)Al2Si2O8 series.
For the obtained series of solid solutions, the unit cell parameters were refined. Samples were recorded in the continuous scan mode of the full X-ray diffraction profile on a PC-HZG-4 automated diffractometer. Angular positions of reflections were estimated by the Spektr-8 program (A. V. Okhulkov, IEM RAS) with correction by the internal standard (spectrally pure Si, a = 5.4305 A). Unit cell parameters (UCP) were refined in terms of the space group C2/m by 30-40 reflections in the angular range of 7-39 degrees ( ) by the LCC and PUDI programs [1]. The calculated values of the unit cell parameters of (Sr,Ba)-feldspars are presented in table:
) by the LCC and PUDI programs [1]. The calculated values of the unit cell parameters of (Sr,Ba)-feldspars are presented in table:
XBaFsp |
a, [A] |
b,[A] |
c, [A] |
|
V, [A3] |
Note |
0.00 |
8.385 |
12.968(1) |
7.131(1) |
115.37(1) |
700.7(1) |
1 |
0.19 |
8.437(1) |
12.986(1) |
7.139(1) |
115.27(1) |
707.3(2) |
1 |
0.45 |
8.501(1) |
12.998(1) |
7.163(1) |
115.16(1) |
716.4(2) |
1 |
0.49 |
8.509(1) |
13.001(1) |
7.163(1) |
115.15(1) |
717.3(3) |
1 |
0.58 |
8.535(1) |
13.011(2) |
7.166(1) |
115.09(1) |
720.7(2) |
1 |
0.80 |
8.598(1) |
13.035(1) |
7.185(1) |
115.08(1) |
729.3(2) |
1 |
1.00 |
8.642(1) |
13.049(1) |
7.204(1) |
115.17(1) |
735.2(1) |
1 |
0.00 |
8.393(1) |
12.972(1) |
7.131(1) |
115.40(1) |
701.3(2) |
2 |
0.21 |
8.437(2) |
12.988(1) |
7.146(2) |
115.33(1) |
707.8(3) |
2 |
0.52 |
8.516(2) |
13.005(2) |
7.169(1) |
115.17(1) |
718.6(2) |
2 |
0.61 |
8.537(1) |
13.014(1) |
7.174(1) |
115.15(1) |
721.5(2) |
2 |
0.83 |
8.587(1) |
13.031(1) |
7.188(1) |
115.14(1) |
728.1(1) |
2 |
1.00 |
8.637(1) |
13.049(1) |
7.207(1) |
115.18(1) |
735.1(2) |
2 |
Note: 1- samples synthesized by annealing mixtures of oxides and carbonates at 1450oC; 2- solid solutions obtained by the hydrothermal treatment (700oC, P = 2 kbar, duration of experiment 12 days) of samples of series 1.
# This work is supported by the Russian Foundation for Basic Research (project N 97-05-65886).
67
Fig.1. (a,b) Concentration dependence of UCP (Sr, Ba)-feldspars: a-parameter a; 1,2 the present work data (1- samples obtained by pyrosynthesis; 2-samples synthesized under hydrothermal conditions; 3-data of Nager; [2], 4-data of Chernyshova et al. [3]). As can be seen in figure, the volumes of mixing of (Sr, Ba)-feldspars obey the Wegard rule, and the excessive mixing volumes are equal to zero.
The values of the parameters obtained in [2] and [3] agree satisfactorily with the results of our calculations.
The concentration dependences of the unit cell parameters were approximated by the third-power polynomials.
a,[A] = 8.3890 + 0.23619.X + 0.02612.X2 - 0.01212114.X3 (+0.005) (1)
b, [A] = 12.9710 + 0.06686.X - 0.008843.X2 + 0.020794.X3 (+0.0030) (2)
c, [A] = 7.1304 + 0.072425.X 0.021725.X2 + 0.66536.X3 (+0.003) (3)
 , [o] = 115.386 0.38417.X 0.48992.X2 + 0.66536.X3 (+0.03) (4)
, [o] = 115.386 0.38417.X 0.48992.X2 + 0.66536.X3 (+0.03) (4)
V, [A] = 700.978 +32.6998 .X + 2.79312.X2 1.379746.X3 (+0.6) (5)
where X is the molar fraction of barium in the solid solution.
For estimation of compositions of binary feldspars by unit cell parameters, the following equation was suggested:
XBaFsp = A + B.(P-M) + C.(P-M)2 + D.(P-M)3 (6)
The coefficients of equation (6) are presented in table:
P |
M |
A |
B |
C |
D |
Ex** |
a, [A] |
8 |
1.47760 |
3.26558 |
2.06385 |
1.751342 |
0.02 |
V, [A3] |
700 |
-0.0231 |
0.029182 |
0.00 |
0.00 |
0.02 |
** is the error of determination of the composition of the solid solution of (Sr,Ba)-feldspar by equation (6).
Conclusions
1. The binary solid solutions of strontium-barium feldspars were synthesized at 700-1400oC. It is shown that in the given temperature range, they exist as continuous solid solutions.
2. Unit cell parameters of (Sr,Ba)-feldspars were refined by the X-ray diffraction method. It is shown that (1) excessive mixing volumes of solid solutions are equal to zero in the whole composition interval; 92) unit cell parameters are independent of the method of synthesis of solid solutions, which indicates indirectly that processes of Al/Si ordering are absent in the temperature range mentioned.
3. For determination of the composition of binary solid solutions, equations were suggested that allow one to estimate compositions from unit cell parameters.
References:
68
#Kotelnikov A.R., Koval'skii A.M., Orlova A.I., Pet'kov V.I., Chichagov A.V., Ushakovskaya T.V. and Ulin I.V. Solid solutions (Na,K)Zr2(PO4)3: experimental study.
key words [zirconium phosphates synthesis]*Institute of Experimental Mineralogy, Russian Academy of Sciences; ; *** Moscow State University
Ceramic materials based on zirconium phosphates (general formula MeI,MeII(MeII,Zr)2(PO4)3, where MeI is Na, K, Rb, Cs, Mg, Ca, Sr, and Ba; MeII is La...Lu, U, Pu...Am) are promising matrices for immobilization of radionuclides of RAW due to their high stability toward leaching processes [1]. Hereinafter, for brevity, we will designate zirconium phosphates as the NZP phase. To predict the behavior of NZP matrices in the Earth crust, one should know their thermodynamic properties and mechanism of cation-exchange reactions with fluid. For this purpose, we performed ion-exchange experiments in the NZP-fluid system under hydrothermal conditions. In the present time, dependences of the parameters on the composition of solid solutions of (Na,K)-containing NZP phases are unavailable. Therefore, we studied solid solutions of NZP by X-ray analysis in order to refine their unit cell parameters (UCP).
Experimental procedure. Experiments were carried out by the ampule procedure in high-pressure installations with a cool gate and external heating. The accuracy of temperature control was +5oC and that for pressure was +50 bar. The duration of experiments was 30-40 days, and the approach to the equilibrium isotherm was performed from two sides. The phase and chemical composition of solid products was analyzed by X-ray and microprobe methods, and solutions were analyzed by atomic-absorption spectroscopy.
Results.
The sodium and potassium distribution in the fluid-(Na,K)Zr2(PO4)3 system was studied at 450-550oC, P = 1-2 kbar in 1 M solutions of (NaCl + KCl). The ion-exchange reactions of the following type were studied:
NaZr2(PO4)3+KCl(fl) = KZr2(PO4)3 +NaCl(fl) (1)
The results of studying reaction (1) are shown in Fig. 1. It is seen that the potassium and sodium distribution between NZP and fluid is not perfect. Potassium enriches the NZP phase relative to the fluid in the whole composition range. The NZP compositions in the products of the same experiment vary within 1-4 mol.%, which indicates that the ion-exchange reaction has occurred completely and the equilibrium in the system has been achieved. The temperature dependence of the distribution is virtually absent. The dependence of the distribution coefficient (KD) on the composition of the solid solution was calculated from the experimental results:
lnKD = 0.0331 + 3.7.XKNZP (450oC) (2)
lnKD = 1.904353 1.366556.XKNZP + 2.872853.(XKNZP)2 (550oC) (3)
Based on this dependence, we calculated the values of parameters of the Margoles model: W1 = W2 = 11.1(3) (450oC), and W1 = 8.4(1); W2 = 1.9(2) kJ/mol (550oC).
X-ray-metry of solid solutions of NZP.
X-ray-metry of the NZP phases was carried out on a PC/HZG-4 automated diffractometer in the continuous scan mode of the complete X-ray diffraction profile. Angular positions of reflections were estimated by the special Spectr-8 program (A. V. Okhulkov, IEM RAS) with correction by the internal standard (spectral pure Si, a = 5.4305 Ao). Unit cell parameters were refined in terms of the R3c space group by 12-17 reflections in the angular interval of 7-39 deg ( ) using the LCC, PUDI [3], and REFLAT programs [4]. Unit cell parameters for terminal terms of the (Na,K)Zr2(PO4)3 series were taken from PDF-2 (ICDD, PDF-2, 33-1312, 35-756).
) using the LCC, PUDI [3], and REFLAT programs [4]. Unit cell parameters for terminal terms of the (Na,K)Zr2(PO4)3 series were taken from PDF-2 (ICDD, PDF-2, 33-1312, 35-756).
The values of UCP of solid solutions of NZP at different molar fractions K are presented in table:
N |
XKNZP |
a, [A] |
c, [A] |
V, [A] |
Ref.* |
1 |
0.00 |
8.803(1) |
22.764(1) |
1527.8(2) |
1 |
2 |
0.00 |
8.80 |
22.86 |
1534.0 |
2 |
3 |
0.00 |
8.8048 |
22.7572 |
1527.88 |
3 |
4 |
0.23 |
8.794(1) |
23.012(5) |
1541.1(3) |
1 |
5 |
0.52 |
8.763(1) |
23.459(4) |
1560.2(3) |
1 |
6 |
0.69 |
8.748(1) |
23.658(7) |
1567.9(4) |
1 |
7 |
0.86 |
8.718(1) |
23.895(5) |
1572.9(3) |
1 |
8 |
0.93 |
8.723(1) |
23.883(3) |
1573.7(2) |
1 |
9 |
0.96 |
8.717(1) |
23.895(4) |
1572.4(3) |
1 |
10 |
0.98 |
8.718(1) |
23.894(4) |
1572.8(4) |
1 |
11 |
1.00 |
8.707(1) |
23.949(5) |
1572.5(5) |
1 |
12 |
1.00 |
8.71 |
23.90 |
1571.0 |
2 |
13 |
1.00 |
8.7191 |
23.9446 |
1576.4 |
3 |
*1 - data of this work; 2 - Pet'kov et al. [2]; 3 - database PDF-2.
# This work is supported by the Russian Foundation for Basic Research (project N 97-05-65886).
69
Fig.1. Isotherms of K distribution in the system NZP-fluid (1Ì solution of NaCl+KCl)
The concentration dependences of UCP of the NZP phases are characterized by nonlinear curves, which are approximated by third-order polynomials:
a = 8.8035 0.019337.X 0.13668.X2 + 0.062019 .X3 [A] (+0.002) (4)
c = 22.7634 + 0.80626.X + 1.61207.X2 1.255468.X3 [A] (+0.02) (5)
V= 1527.8 + 49.2417.X + 54.4101 .X2 59.9886.X3 [A] (+0.2) (6)
where X is the molar fraction of potassium in the solid solution of NZP.
The excessive mixing volume of the solid solution of NZP was described in terms of the biparametric Margoles model: W1 = 49.5(4) and W2 = 14.4(3) [A3].
Discussion. Based on the results obtained, we can conclude that the behavior of the solid solution of NZP at 450-550oC is not perfect. The nonideal character of mixing decreases as the temperature increases, which is indicated by a smoother slope of the curve of the lnKD-composition dependence. At the same time, asymmetry of the excessive mixing energy correlates well with the asymmetrical curve of the excessive mixing volume (the maximum of the mixing functions is at XKNZP = 0.625).
As said above, the NZP phases are potential matrices for immobilization of radionuclides. Therefore, the study of exchange reactions in the NZP-fluid systems gives information on their behavior during prolonged placement in Earth crust rocks in the matrix-solution-host rock system.
References:
#Kotel'nikov A.R., Koval'skii A.M., and Akhmedzhanova G.M. Experimental study of solid solutions (Sr,Ba)CO3.
key words [Sr,Ba carbonates fluid experiment]
Strontium and barium carbonates (strontianite and witherite) are abundant minerals of hydrothermal deposits. Isomorphous substitutions Sr <-> Ba within sufficiently wide limits (to tens mol.%) are observed in natural samples of these minerals. However, the problem about the existence of the immiscibility region of their solid solutions is still unclear. Physicochemical parameters of isomorphous substitutions are poorly studied. Previously, the properties of solid solutions strontianite-witherite synthesized at relatively high (800oC) temperatures have been studied by X-ray-metry and thermochemically [1, 2]. A considerable deviation from perfectness for isomorphous substitutions in binary solutions of (Sr,Ba)-containing carbonates has been shown. This fact suggested the possible existence of solvus in the strontianite-witherite system at low temperatures. To estimate the properties of solid solutions of (Sr,Ba)containing carbonates, we performed experimental studies of synthesis of solid solutions and cation-exchange equilibria in a wide temperature range from 400 to 800oC.
Experimental. Starting materials. Pure (special chemical purity) reagents of SrCO3 and BaCO3 and their mixtures were used as the starting materials. Solutions were prepared from the reagents (special chemical purity) of SrCl2.6H2) and BaCl2.2H2O and distilled water. Solutions with 0.5 M concentrations were mainly used.
Equipment. Experiments were carried out on hydrothermal installations with a cool gate and external heating. The accuracy of temperature control was +5oC, and that for pressure was +50 bar.
Experimental procedure. Experiments on synthesis of solid solutions and studying cation-exchange reactions in the carbonate-fluid system were carried out by the ampule procedure, The approach to equilibrium was performed, as a rule, from two sides. The duration of experiments was varied from 60 (at 400oC) to 14 (at 800oC) days. After exposure in the experimental regime, the ampules were opened, and the solution was filtered to separate the weighed sample.
# This work is supported by the Russian Foundation for Basic Research (project N 97-05-65886).
70
Analytical procedures. The products of experiments were analyzed as follows: a solution, by atomic-absorption spectroscopy; solid solutions of carbonates, by the microprobe and X-ray methods. According to the X-ray analysis data, the products of experiments contained solid solutions of (Sr,Ba) carbonates. In the X-ray study, for the calculation of unit cell parameters (UCP), the cobalt radiation was used, and spectral pure silicon was used as the internal standard. On the average, 20-30 reflections within the angle interval of 7-39 deg ( ) were used for the calculation of UCP. The parameters were calculated using the LCC, PUDI [3], and REFLAT [4] programs.
) were used for the calculation of UCP. The parameters were calculated using the LCC, PUDI [3], and REFLAT [4] programs.
Fig.1. Ba partitioning between solid solution of strontium barium carbonates and fluid
Results and discussion. The strontium and barium distributions in the carbonate-fluid system at 400, 600, 700, and 800oC are shown in Fig. 1. The cation-exchange reaction between carbonate and fluid is written in the form:
SrCO3 + BaCl2 =BaCO3 + SrCl2 (1)
In the temperature range studied, strontium-barium carbonates form continuous series of solid solutions. The temperature dependence of the barium distribution between carbonate and fluid is almost absent (Fig. 1). Barium enriches the fluid relative to the carbonate solid solution in the whole composition range. Based on the experimental data on the strontium and barium distribution between carbonate and fluid, we can estimate the excessive mixing energies of solid solutions (accepting the fluid as the perfect solution). The peculiarities of the dependence of the lnKD function on the composition of carbonate (and fluid) make it possible to consider the strontianite-witherite solid solution to be regular; therefore, it is described in terms of the monoparametric Margoles model. Since the temperature dependence is virtually absent, the Margoles parameter for 700oC was estimated: W = 11.5(9) kJ/mol. The mean value of the Margoles parameter by the estimations at all temperatures is equal to 12.1(12)kJ/mol. Refinement of unit cell parameters of solid solutions of (Sr,Ba) carbonates. The results of calculations of UCP from the data of our work are presented in table:
XBaCb |
a, [A] |
b, [A] |
c, [A] |
V, [A3] |
0.003 |
5.109(4) |
8.418(3) |
6.031(2) |
259.4(4) |
0.006 |
5.110(4) |
8.417(3) |
6..033(3) |
259.5(5) |
0.012 |
5.102(3) |
8.414(5) |
6.042(2) |
259.3(2) |
0.020 |
5.105(3) |
8.415(4) |
6.038(3) |
259.4(2) |
0.030 |
5.105(6) |
8.420(8) |
6.058(5) |
260.4(3) |
0.120 |
5.129(1) |
8.470(1) |
6.086(1) |
264.4(1) |
0.160 |
5.140(1) |
8.486(1) |
6.102(1) |
266.1(1) |
0.180 |
5.143(2) |
8.508(2) |
6.110(1) |
267.3(2) |
0.440 |
5.195(1) |
8.638(2) |
6.237(1) |
280.0(1) |
0.450 |
5.200(1) |
8.626(2) |
6.241(1) |
280.0(2) |
0.520 |
5.213(2) |
8.659(3) |
6.262(1) |
282.7(2) |
0.870 |
5.283(1) |
8.825(2) |
6.394(2) |
298.1(2) |
0.905 |
5.293(1) |
8.848(2) |
6.400(1) |
299.7(1) |
The unit cell volume of the strontianite-witherite series obeys the Wegard rule (excessive mixing volume is equal to zero).
The concentration parameters of unit cells of solid solutions are described by the following equations:
a = 5.10529 + 0.207694.X[A] (2)
b = 8.41203 + 0.481833.X[A] (3)
c = 6.03089 + 0.496647.X 0.094065.X2[A] (4)
V = 259.141 + 45.1853.X[A3] (5)
Conclusions.
1. The solid solutions of (Sr,Ba)-containing carbonates were studied at 400-800oC and 1-2 kbar by synthesis and cation-exchange reactions. Strontium-barium carbonates were shown to form continuous series of solid solutions in the temperature range studied.
2. The barium distribution between carbonate and fluid was shown to be nonideal: barium enriches the fluid relative to carbonate in the whole composition range. The temperature dependence of the barium distribution between carbonate and fluid is almost absent. Based on the data on strontium and barium distribution between carbonate and fluid, the Margoles parameter for the regular solution was calculated: W = 11.5(9) kJ/mol.
3. Unit cell parameters of witherite-strontianite solid solutions were refined. The dependences of the parameters on the composition were shown to be linear (and sublinear). The mixing volume obeys the Wegard rule. Thus, the solid solutions (Sr, Ba)CO3 are characterized by energy imperfectness of mixing (Ge and He values differ from zero), while the mixing imperfectness is absent at the crystallochemical level (Ve = 0).
71
References:
#Koval'skii A.M., Kotelnikov A.R. and Ogorodova L.P. Thermochemical study of solid solutions of (Na,Sr)-feldspars.
key words [Na,Sr-feldspars thermochemical data]
*Institute of Experimental Mineralogy, Russian Academy of Sciences, 142432 Chernogolovka, Moscow Region ; ** Moscow State University, Department of Geology, 119899 Moscow, Vorob'evy Gory
Statement of problem. Feldspars are framework alumosilicates, which are main rock-forming materials. Feldspars are the unique object for thermodynamic studies due to their wide limits of isomorphous substitutions. Substituting isomorphically cations in the composition of feldspars almost without changing their structural type, one can obtain information for development of thermodynamic models of their solid solutions.
Synthesis of samples of solid solutions of (Na,Sr)-Feldspars. Several procedures were developed for the synthesis of solid solutions of (Na,Sr)-feldspars. The best results (homogeneity of products of the synthesis and their correspondence to the starting compositions) were achieved by using the following methods: (1) devitrification of glasses with the corresponding composition under hydrothermal conditions followed by recrystallization of heterogeneous products of the first experiments (700oC, P = 1 kbar); (2) pyrosynthesis from mixtures of carbonates and oxides under dry conditions (1400-1450oC); (3) hydrothermal recrystallization of products of pyrosynthesis (700oC, P = 1 kbar); (4) cation-exchange reactions (700oC, P = 1.5-2 kbar).
Glasses of feldspars and mixtures of carbonates and oxides (Na2CO3, SrCO3, Al2O3, and SiO2) taken in stoichiometric ratios were used as the starting materials for experiments on synthesis of (Na,Sr)-feldspars.
The compositions of the synthesized feldspars according to the data of microprobe studies and recalculations of the compositions to crystallochemical formulas are presented in table:
Entry no |
XSrFsp | SiO2 | Al2O3 | CaO | Na2O | K2O | SrO | Crystallochemical formula |
| 4490 | 0.0 | 69.65 | 18.95 | - | 11.36 | 0.02 | - | Na0.96Al0.97Si3.03O8 |
| 4732 | 0.175 | 62.34 | 21.38 | - | 9.61 | - | 6.82 | Na0.85Sr0.18Al1.15Si2.84O8 |
| 4671 | 0.18 | 61.68 | 22.26 | - | 9.10 | 0.09 | 6.87 | Na0.80Sr0.18Al1.20Si2.81O8 |
| 4676 | 0.26 | 59.63 | 22.59 | - | 8.09 | - | 9.70 | Na0.73Sr0.26Al1.23Si2.76O8 |
| 4262 | 0.45 | 53.61 | 23.39 | - | 6.81 | - | 16.14 | Na0.64Sr0.45Al1.34Si2.61O8 |
| 4263 | 0.51 | 51.46 | 25.07 | 0.03 | 5.12 | 0.03 | 18.18 | Na0.49Sr0.51Al1.45Si2.53O8 |
| 4669 | 0.62 | 48.15 | 26.41 | - | 3.93 | 0.11 | 21.33 | Na0.38Sr0.62Al1.56Si2.42O8 |
| 4301 | 1.0 | 35.72 | 30.18 | 0.12 | 0.05 | - | 29.26 | Sr0.95Al2.01Si2.01O8 |
| 4713 | 1.0 | 36.67 | 30.27 | - | - | - | 33.06 | Sr1.05Al1.96Si2.01O8 |
"-" means that the element was not detected by the analysis.
X-ray study of synthesized (Na,Sr)-feldspars. The X-ray phase analysis of samples showed a high degree of their crystallinity and appropriate character for refinement of unit cell parameters. Samples of (Na,Sr)-feldspars were homogeneous in composition, and the content of admixtures did not exceed 3-5%. The unit cell parameters were calculated by the least-squares method using the PUDI, LCC (Bernem, 1991) and IND1, KRIST computer programs (developed by NPO "Burevestnik," Leningrad). On the average, from 24 to 35 reflections were used to refine UCP. It was accepted in calculations of UCP that at XSrFsp > 0.35 the structure of (Na,Sr)-feldspars corresponds to the C2/m type (monoclinic), and at XSrFsp < 0.35, it corresponds to the C1 type (triclinic).
The results of refinement of unit cell parameters of feldspars at 20oC synthesized in this work are presented in table:
Entry no. |
XsrFsp | a, [A] | b, [A] | c, [A] |  , [A] , [A] |
 , [A] , [A] |
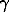 ,[A] ,[A] |
V, [A3] | ||
| 4490 | 0.0 | 8.159(5) | 12.870(4) | 7.109(3) | 93.493(24) | 116.467(28) | 90.201(48) | 666.59(35) | ||
| 4671 | 0.18 | 8.211(1) | 12.925(1) | 7.144(1) | 91.919(6) | 116.275(6) | 90.296(7) | 679.26(16) | ||
| 4676 | 0.26 | 8.236(2) | 12.964(3) | 7.155(1) | 90.248(23) | 116.139(11) | 90.103(24) | 685.87(27) | ||
| 4262 | 0.45 | 8.261(3) | 12.965(3) | 7.132(2) | 90 | 115.732(18) | 90 | 688.12(51) | ||
| 4263 | 0.51 | 8.259(1) | 12.963(1) | 7.152(1) | 90 | 115.981(9) | 90 | 688.29(24) | ||
| 4669 | 0.62 | 8.287(1) | 12.968(1) | 7.151(1) | 90 | 115.638(8) | 90 | 692.83(22) | ||
| 4301 | 1.0 | 8.391(3) | 12.968(4) | 7.128(4) | 90 | 115.369(27) | 90 | 700.87(55) | ||
| 4713 | 1.0 | 8.395(1) | 12.974(1) | 7.130(1) | 90 | 115.409(7) | 90 | 701.49(19) | ||
The values obtained correlate well with the data of Bambauer et al. (1984) and Kotelnikov and Kotelnikova (1996).
# This work is supported by the Russian Foundation for Basic Research (project N 97-05-65886).
72
Thermochemical study of (Na,Sr)-feldspars. The study was performed in the laboratory of experimental thermodynamics of minerals (Department of Geology, Moscow State University) by high-temperature calorimetry of dissolvation at 700oC on a differential heat conducting Calvet microcalorimeter (Setaram).
The calorimetric measurements gave enthalpies of dissolvation of solid solutions of (Na,Sr)-feldspars with XSrFsp = 0.0, 0.175, 0.51, 0.62, and 1.0. The excessive enthalpies of mixing for the available solid solutions were determined from these data using the equation:
 Hmix = (
Hmix = ( Hsol A . XA +
Hsol A . XA +  HsolB .XB) -
HsolB .XB) -  Hsolss
Hsolss
The experimental values of enthalpies of dissolvation and excessive enthalpies of mixing of the solid solutions of (Na,Sr)-feldspars are presented in table:
Entry no |
XsrFsp |  Hsol700oC (kJ/mol) Hsol700oC (kJ/mol) |
 Hmix700oC (kJ/mol) Hmix700oC (kJ/mol) |
| 4490 | 0.0 | 66.16 + 4.24 (8) | - |
| 4732 | 0.175 | 70.28 + 4.48 (3) | -0.93 |
| 4263 | 0.51 | 79.66 + 3.32 (7) | -4.21 |
| 4669 | 0.62 | 78.48 + 3.71 (8) | -1.02 |
| 4713 (pyrosynthesis) | 1.0 | 87.68 + 2.42 (5) | - |
| 4713 (pyrosynthesis + hydrothermal treatment) | 1.0 | 84.38 + 6.11 (4) | - |
The data obtained coincide well (within measurement errors) with the data obtained by Valyashko (1988).
Thermodynamic treatment of experimental results. The analysis of the results obtained on high-temperature dissolvation of solid solutions of (Na,Sr)-feldspars and the calculation of excessive enthalpies of mixing allow one to consider the system to be close to the perfect one with the negative deviation of Hex from perfectness.
The excessive enthalpy of mixing of solid solutions of (Na,Sr)-feldspars can be described by the biparametric Margoles model according to the equation:
Hex = XSrFsp . (1-XSrFsp)2 . W2 + (1-XSrFsp).( XSrFsp)2 . W1
The model has the following parameter:
W1 = -8.3(4.1), W2 = -12.9(6.2)
References :
#Bekker R.B., Demin S.P., Foursenko D.A., Thomas V.G. Modeling of pulsing heat- mass exchange processes in an autoclave at hydrothermal crystal growth.
key words [crystal growth zoning temperature pulsation]
Institute of Mineralogy and Petrography SB RAS
Beryl crystals, grown by us under hydrothermal conditions, exhibit a pronounced growth zoning in parallel with the growth front. The interzonal boundaries are sharp despite the fact that a mean temperature of the autoclave Tav was maintained within +0.2oC during the growth cycle. In this work we check whether such pulsations are able to cause the appearance of zoning in crystals or, else, zoning is due to other factors, for example, uncontrolled temperature pulsations inside the autoclaves due to the turbulent character of heat- mass exchange [1].
In order to investigate Tm pulsations as the reason for the growth zoning, beryl crystals were grown under the conditions of sinusoidal pulsations (of various amplitude and frequency) of the growth temperature. The revealing in a nonperiodic growth zoning, typical for hydrothermal beryls, of a periodic component having the frequency complying with the temperature pulsation frequency ought to unambiguously indicate that the zoning is induced by such sinusoidal temperature pulsations. The crystals were grown by a temperature gradient method ( T=70oC) at 600oC, the rates being about 0.25 mm/d. The ground sections produced from the grown crystals were examined by a shadow method. The numbered optical density values with respect to the profile in parallel with the crystal growth direction were subjected to the Fourier analysis.
T=70oC) at 600oC, the rates being about 0.25 mm/d. The ground sections produced from the grown crystals were examined by a shadow method. The numbered optical density values with respect to the profile in parallel with the crystal growth direction were subjected to the Fourier analysis.
It was been found that the temperature pulsations with the period τ>6h, amplitude A>1oC and the ratio A/τ>0.167 deg/h are fixed in hydrothermally grown beryl crystals as a periodic growth zoning. An increase in the temperature pulsation period results in zoning periodicity losses. However, higher-frequency temperature pulsations are also fixed in crystals that is attested by the appearance of the diffraction grating on the crystal sections grown at temperature pulsation with A=1oC and τ=0.5 h. So, the non-periodic zoning observable in batch-produced beryl crystals cannot be attributed to Tm pulsations in the autoclave as the requirement A>1oC is not fulfilled for them.
# This work is supported by the Russian Foundation for Basic Research (project N 98-05-65196). The technical aid in design and fabrication of the experimental equipment was rendered by the JV Tairus.
73
Modelling of the temperature pulsations inside the autoclaves caused by a turbulent character of the heat- mass exchange was performed under normal pressure on a vertical planar layer (VPL) [1] filled with distilled water (the water column height was 290 mm). We modelled a planar pattern of heat-mass exchange in the vertical axial section of the autoclave placed in a thermal field symmetrical with respect to the autoclave axis, the vertical temperature gradient being positive (the temperature of the autoclave bottom is higher than that of its top). The temperatural difference in the VPL was preset with a bottom heater to be 14oC at the side VPL wall. The heater temperature accuracy was maintained within +0.1oC. The temperature inside the VPL was measured along its axis with a chramel-alumel differential thermocouple as a temperature difference ( T) between the immobile junction fixed at a height of 10 mm from the VPL bottom and the mobile junction movable along the VPL axis. The accuracy of the
T) between the immobile junction fixed at a height of 10 mm from the VPL bottom and the mobile junction movable along the VPL axis. The accuracy of the  T measurement was +0.05oC. The measurements were performed in 6 points of the VPL axis for the mobile thermocouple junction position being as high as 20,80, 140, 180, 230 and 280 mm from the VPL bottom. 163840 were counted in each point at a meter inquiry frequency 16 meas/s.
T measurement was +0.05oC. The measurements were performed in 6 points of the VPL axis for the mobile thermocouple junction position being as high as 20,80, 140, 180, 230 and 280 mm from the VPL bottom. 163840 were counted in each point at a meter inquiry frequency 16 meas/s.
The experiments have shown that pulsations of a  T value of various frequencies, amplitudes and periodicity degrees are observed in the VPL. One can distinguish nonperiodic high-frequency (period =10s) pulsations with the amplitude to 2.5oC, periodic (periodicity was revealed by a Fourier analysis of a
T value of various frequencies, amplitudes and periodicity degrees are observed in the VPL. One can distinguish nonperiodic high-frequency (period =10s) pulsations with the amplitude to 2.5oC, periodic (periodicity was revealed by a Fourier analysis of a  T value), mean frequency pulsations (period 1-2 min) with the amplitude =5 oC, and nonperiodic low-frequency (period 0.5-1h) ones with the amplitude to 0.3oC. The averaged temperature difference between the points 20 and 280 mm high from the VPL bottom amounts to 0.5+0.1oC which is coincident with the double amplitude of the low frequency pulsations of the
T value), mean frequency pulsations (period 1-2 min) with the amplitude =5 oC, and nonperiodic low-frequency (period 0.5-1h) ones with the amplitude to 0.3oC. The averaged temperature difference between the points 20 and 280 mm high from the VPL bottom amounts to 0.5+0.1oC which is coincident with the double amplitude of the low frequency pulsations of the  T and is one order smaller against that for high-frequency pulsations.
T and is one order smaller against that for high-frequency pulsations.
Lower viscosity of real hydrothermal solutions as compared with water suggests greater turbulency of heat-mass exchange in the autoclave compared to VPL, therefore the same order temperature pulsations take place in the autoclave during crystal growth. The similarity of the critical values of the A and A/τ temperature pulsations, fixed in beryl crystals as the growth zoning, with such for temperature pulsations observable in the vertical planar layer is suggestive of the fact that precisely these pulsations are responsible for the occurrence of the growth zoning.
Reference:
Dorogokupets P.I., Ponomarev E.M. Specific heat and thermal expansion of minerals: new approach.
key words [thermal expansion heat capacity calculation]
Specific heat at constant pressure and thermal expansion coefficient dictate thermal corrections in the equations of state of substances, and their reliability governs the precision of calculation of thermodynamic functions at elevated T and P. In the literature the greatest attention was paid to representation of specific heat and thermal expansion coefficient through individual equations, although the works are available whose authors posed the problem of a simultaneous congruence of specific heat at constant pressure, thermal expansion coefficient, and isothermal compression modulus [Saxena, 1988, Doroshev et al, 1988, Gillet et al., 1991 and others].
The relationship between specific heat and thermal expansion coefficient can be written as [Slater, 1939]:
CP = CV +  2VoTKTo + VoTKTo
2VoTKTo + VoTKTo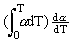 (1)
(1)
where Cv is specific heat at constant volume, Vo is the volume at 0 K, V is the volume, KTo is the isothermal compression modulus at 0 K,  is the thermal expansion coefficient. The equation (1) goes into the classic thermodynamic relationship at the constancy of the thermal expansion coefficient, that is valid for every isotherm
is the thermal expansion coefficient. The equation (1) goes into the classic thermodynamic relationship at the constancy of the thermal expansion coefficient, that is valid for every isotherm
CP = CV +  2VTKT (2)
2VTKT (2)
We assume that the equation (1) is valid in a rather broad temperatural range and we exclude from it the compression modulus KTo by representing it via the Gruneisen parameter. Then we obtain:
CP = CV(1 + 
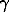 oT +
oT + 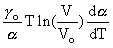 ) (3)
) (3)
where 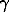 o is the Greneisen parameter at 0 K.
o is the Greneisen parameter at 0 K.
Now the specific heat at constant volume is determined via the specific heat at a constant pressure, the thermal expansion coefficient and the volume which, in a way, are temperature dependent, and the Gruneisen parameter at 0 K.
We shall consider the specific heat at constant volume as a carrier function and define it via the Nernst-Lindemann function [Wachtman et al., 1962]:
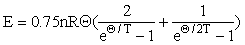 (4)
(4)
the derivative of which is close to the Debye specific heat in the region Θ/T <5-10.
We represent the dependence of the volume on the energy in Suzuki's approximation [Suzuki, 1975]:
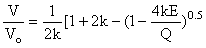 (5)
(5)
74
where k=(K-1)/2 and by differentiating we find  (T) and d
(T) and d /dT. The analogous dependencies can be derived from the approximation [Wachtman et al., 1962] which we already considered [Dorogokupets, Ponomarev, 1998]. The equations (3-5) and their derivatives govern the temperature dependence of the specific heat at constant pressure and the thermal expansion coefficient, and can be optimized by a least squares technique with a balance. The normalized coefficient between the specific heat and thermal expansion coefficient is taken to be VoT
/dT. The analogous dependencies can be derived from the approximation [Wachtman et al., 1962] which we already considered [Dorogokupets, Ponomarev, 1998]. The equations (3-5) and their derivatives govern the temperature dependence of the specific heat at constant pressure and the thermal expansion coefficient, and can be optimized by a least squares technique with a balance. The normalized coefficient between the specific heat and thermal expansion coefficient is taken to be VoT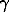 o . In the range of the Debye temperatures and higher the accuracy of determination of Cp(T) is several times in excess of the accuracy of determination of
o . In the range of the Debye temperatures and higher the accuracy of determination of Cp(T) is several times in excess of the accuracy of determination of  (T), one, therefore, can define the weight of the data to be 10.
(T), one, therefore, can define the weight of the data to be 10.
Having optimized Cp and  (T), one can calculate other thermal physical functions from the independent determinations of the adiabatic compression modulus, for example, from the data (Anderson, Isaak, 1995) for some minerals. These quantities can be represented via the volume and the Anderson-Gruneisen parameter
(T), one can calculate other thermal physical functions from the independent determinations of the adiabatic compression modulus, for example, from the data (Anderson, Isaak, 1995) for some minerals. These quantities can be represented via the volume and the Anderson-Gruneisen parameter  s.
s.
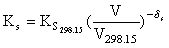 (6)
(6)
Having done this, we find the Greneisen parameter 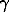 =
= KsV/Cp and then we calculate the real values of CV and KT.
KsV/Cp and then we calculate the real values of CV and KT.
The model was tested on metals, oxides, and minerals. For example, for periclase we obtained: Vo=11.195 cm3, Θ=757K, KTo=86.9 GPa, 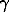 o=0.864, k=1.44, Ks = 298.15 =164.7 GPa,
o=0.864, k=1.44, Ks = 298.15 =164.7 GPa, 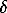 s=3.1, which govern the thermodynamic functions in the range from 300 K to the melting temperature (Table 1 and fig.1).
s=3.1, which govern the thermodynamic functions in the range from 300 K to the melting temperature (Table 1 and fig.1).
Fig.1. Thermal expansion of periclase. Experimental data: Skinner [1957]; Suzuki [1975]; Dubrovinsky, Saxena [1997]. S-fit calculated using equation (5); W-fir-calculated using Wachtman et al. [1962] equation [Dorogokupets, Ponomarev, 1998].
Fig.2. Calculated heat capacity of periclase.
Table 1. Computed thermophysical functions of periclase, MgO
| T, K |  , K-1 , K-1 |
V/Vo | CP, J.mol-1K-1 | KS, Gpa | 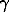 |
CV, J.mol-1K-1 | KT , MPa |  KT, K-1 MPa KT, K-1 MPa |
| 298.15 | 3.30E-05 | 1.00475 | 37.21 | 164.7 | 1.643 | 36.62 | 162.0 | 5.35 |
| 500 | 4.05E-05 | 1.01237 | 45.37 | 160.9 | 1.626 | 43.92 | 155.7 | 6.30 |
| 1000 | 4.62E-05 | 1.03480 | 50.61 | 150.3 | 1.590 | 47.14 | 140.0 | 6.47 |
| 1500 | 4.99E-05 | 1.05997 | 52.98 | 139.5 | 1.559 | 47.45 | 124.9 | 6.23 |
| 2000 | 5.42E-05 | 1.08786 | 55.46 | 128.7 | 1.531 | 47.57 | 110.4 | 5.98 |
| 2500 | 6.01E-05 | 1.11926 | 58.98 | 117.8 | 1.503 | 48.12 | 96.1 | 5.77 |
| 3000 | 6.94E-05 | 1.15583 | 65.24 | 106.7 | 1.468 | 49.98 | 81.7 | 5.67 |
References:
75
#Kiseleva I.A.1, Melchakova L.V.1, Ogorodova L.P.1, Belitsky I.A.2, Fursenko B.A.2 Thermodynamic properties of bikitaite.
key words [bikitaite enthalpy]
Bikitaite is zeolite of the mordenite group. We have studied a natural sample of the composition Li2.10Al2.00Si3.97O12.1.95H2O. As suggested by the thermal analysis data bikitaite is stable to 420K. Dehydration occurs in one stage with the maximum at 570K and is completed at 720K. The thermal curve is analogous to that reported by Gottardi and Galli [1].
The studies were conducted on a differential scanning calorimeter (DSC) 'Mettler TA-2000B', Switzerland [2] and on a Calvet heat flux high-temperature microcalorimeter 'Setaram', France [3].
The specific heat of bikitaite was measured on a DSC within 110-420K (to the dehydration onset temperature) in nitrogen at a heating rate 10K/min and cooling rate 5K/min. In the negative temperature region bikitaite demonstrated the reversible phase transition documented on the cooling and heating curves(DTA) and by the specific heat measurements. The phase transition occurs on a narrow temperature range (about 15K) with Tmax= 225K. The maximal excessive specific heat of the transition was about 11.0 J/mol.K for the composition Li2[Al2Si4O12].2H2O. Corrections for the deviation of the bikitaite composition from the ideal one were within the experimental inaccuracy.
The experimental data on specific heat in the range from room temperature to the dehydration temperature (420K) were used to calculate the equation Cop=151.85 + 669.87.10-3.T 1.63.105.T2 (J/mol.K); Cop,298.15=349.84 (J/mol.K). The maximal approximation error was 1.98%.
A double-drop method was used to determine the dehydration enthalpy of bikitaite on a Calvet microcalorimeter. The dehydration enthalpy made up 58.2+15.4 kJ/mol. In order to obtain the formation enthalpy a method of drop solution into a melt of the composition 2PbO.B2O3 was used at T=973 K.
The formation enthalpy of bikitaite from the elements was calculated from three exchange reactions with the participation of fluorides:
Al2O3(k) + 4SiO2(k) + 2H2O(l) + CaO(k) + 2LiF(k) = =Li2Al2Si4O12.2H2O(k) +CaF2(k)
 Hof,298.15(1) =-6711.0+15.1 kJ/mol;
Hof,298.15(1) =-6711.0+15.1 kJ/mol;
Al2O3(k) + 4SiO2(k) + 2H2O(l) + Na2O(k) + 2LiF(k)= =Li2Al2Si4O12.2H2O(k)+2NaF(k)
 Hof,298.15(2) =-6696.9+13.4 kJ/mol;
Hof,298.15(2) =-6696.9+13.4 kJ/mol;
4Al2O3(k) + 12SiO2(k) + 6H2O(l) + 6LiF(k)= =3Li2Al2Si4O12.2H2O(k)+2AlF3(k)
 Hof,298.15(3) =-6706.2+13.8 kJ/mol.
Hof,298.15(3) =-6706.2+13.8 kJ/mol.
The calculated enthalpy values of bikitaite formation from elements are in agreement with each other. A mean of these values, -6704.7+8.2 kJ/mol, can be recommended for thermodynamic calculations.
References:
Smirnov S.Z.1, Thomas V.G.1, Demin S.P.1, Vidik S.V.2 Conditions and mechanism of formation of solution inclusions in regeneration sectors of synthetic beryl crystal.
key words[synthetic beryl solution inclusions]
Institute of Mineral and Petrography SB RAS Novosibirsk 630090 Koptyuga pr., 3; Novosibirsk State University 630090 Koptyuga pr., 2
In order to reconstruct the mechanisms of trapping the solution inclusions, we have studied crystals of synthetic beryl grown from hydrothermal solutions of various compositions. The seeds were synthetic beryl plates in parallel with (5.5.10.3), (1120), and (1121) planes.
Crystal morphology, microrelief of the growth surfaces, structure of the regeneration sectors, features of morphology, and arrangement of mineral-forming solution inclusions in the crystal were studied by methods of optical microscopy and goniometry. The compositions of the solution inclusions and of the residual solution from the autoclave were studied cryometrically.
It has been found that regeneration of the seeds in parallel with (1120) and (1121) like the growth of the other singular faces appearing on the crystal, do not give rise to primary inclusions. Alternatively, the regeneration sectors of the non-singular (5.5.10.3) surface concentrate all the trapped solution inclusions. The latter is due to specific features of the growth processes which form its macro- and microrelief.
The regeneration (5.5.10.30) surface has a linear-cellular structure dictated by the occurrence of systems of ridge-like subindividuals whose faces grow preferentially by the tangential mechanism. At small growth rates the generating sites locate in depressions between two neighbouring subindividuals whose faces have an even or a slightly curved profile. As the growth rate is increased, the faces of the subindividuals acquire a convex profile, and the generating sites locate near their ridges. This, in our opinion, is a consequence of an enhancement of the supersaturation gradient between the ridge and the base of the subindividuals. The intermediate situation where the growth centers occur both in depressions and on ridges also takes place. The differences in the growth centers account for the formation of inclusions of two different types. Inclusions of the first type characteristic of beryl crystals growth at relatively small rates (0.1-0.2 mm/d) are needle-shaped. Their formation is the consequence of enveloping of foreign particles, occurring in regeneration surface depressions, by growth steps of the subindividuals faces.
The coalescence of the step ends gives rise in the vicinity of the particle to surfaces subparallel with prismatic {1010} faces having very low growth rates (Shatsky et al, 1980; Lebedev, Askhabov, 1984). As a result, in parallel with the 6-th order axis there forms a channel-like narrowing cavity in the base of which the trapped particle locates.
# This work is supported by the Russian Foundation for Basic Research (project N 98-05-64219).
76
Beryl crystals grown at relatively high rates (about 0.3 mm/d and higher) exhibit inclusions of the second type. These are large flat inclusions of, mainly, irregular shape oriented in parallel with the (1100) face. Their trapping is conditioned by the formation of slit-like cavities between large subindividuals having concave faces.
The cavity thickness being much smaller compared with the rest of the dimensions, the conservation of the inclusions occurs by the mechanism of crack healing (Lammlein, 1973). It should also be mentioned that ingress of crystalline particles onto the (5.5.10.3) surface, growing at a high rate, is, almost, not accompanied by the formation of needle-like inclusions.
In addition to the reasons conditioned by the supersaturation gradient at the growth front, the formation of inclusions in regeneration sectors of beryl is greatly affected by the occurrence of Fe2+ in the solution, on the contrary, is of no significant effect either on the growing regeneration surface morphology, or on trapping the inclusions. As the Fe2+ concentrations acquire a columnar shape and prismatic {1010} faces appear on them giving rise to rough depressions of various shapes.
Cryometric studies show that the chemical composition of inclusions, is, within the methods precision, indentical to the composition of the initial solution.
This fact and our results, showing that dissolution of beryl in the employed range of temperatures and pressures occurs congruently, do not allow us to regard the concentration of impurities at the growth front as the reason for the inclusions formation.
The afore data suggest the following conclusions:
1) The formation of inclusions in the studied beryl crystals proceeds at the development of nonsingular regeneration surfaces since they are less stable morphologically, as compared with singular surfaces.
2) The general reason for trapping inclusions at the growth of the (5.5.10.3) surface is the manifestation in the morphology of subindividuals of beryl growth rate anisotropy. As the orientation of some vicinal surfaces of the subindividuals approaches the {1010} prism, their growth rate decelerates appreciably as compared with the remaining directions. The growth rate of the [1010] (=0.01 mm/d) is at least one order of magnitude lower than the growth rates of the faces orientationally close to bipyramids or to a second order {1120} prism.
At low rates faces close to {1010} appear where the growing surface envelopes a foreign particle. At higher rates and at a hindered convection these faces appear as a result of advancing growth of regions close to the subindividual ridges as compared to the regions in the vicinity of the depressions.
The presence of divalent cations in the solution enhances the growth rate anisotropy of beryl (Shatsky et al, 1981) and leads to the appearance of prismatic {1010} faces in subindividuals which contributes to the regeneration surface relief disintegration and, therefore, the inclusion formation.
References:
#Vilisov V.A.1, Moloshag V.P1. Vilisov D.V.2, Fedorenko V.V.2 Quantitative XES determination of the oxidation degree of iron and chromium in chromspinelides.
key words [iron chromium chrom spinelide oxidation]
1 Institute of Geology and Geochemistry UB RAS; 2-D.V. Vilisov, V.V. Fedorenko. Institute of Metal Physics, UB RAS.
One of the key parameters that determine the formation conditions of mantle rocks is oxygen fugacity. Mineralogic methods of oxybarometry based on quantitative ratios of iron of dissimilar valencies in chromspinelides are most recognized. The use of the X-ray emission spectroscopy (XES) for the determination of dissimilar-valence forms of iron is dictated by its locality and the possibility to obtain information on not only the chemical composition of samples but, also, the character of bonds between elements and their coordination environment [1]. In view of the fact that the occurrence of divalent and trivalent chromium [2] as well as the difference in its coordination environment were found in synthetic chromspinelides by other methods, [2,3], it has been our goal to obtain similar results for natural chromspinelides using XES method.
X-ray emission spectra of iron and chromium FeL ,
, and CrL
and CrL ,
, (2p3/2,1/2
(2p3/2,1/2  3d4s transition) were taken on electron-probe microanalyser 5 JCXA-733 with a completely focused spectrometer (Johann type) and a crystal analyzer TAP (acidic thallium phthalate, 2d=25.76A) curved in the radius R=140mm. The spectrometer slit was 0.3mm, the energy resolution was about =0.8 ev in the region of CrL
3d4s transition) were taken on electron-probe microanalyser 5 JCXA-733 with a completely focused spectrometer (Johann type) and a crystal analyzer TAP (acidic thallium phthalate, 2d=25.76A) curved in the radius R=140mm. The spectrometer slit was 0.3mm, the energy resolution was about =0.8 ev in the region of CrL ,
, lines, and about =2.2 ev in the region of Fe L
lines, and about =2.2 ev in the region of Fe L ,
, lines. The improved spectrometer resolution for detecting the chromium spectrum makes it possible to compare chromium spectra with those of other copounds. The X-ray exitation conditions were V=15 kev, I= 1.5 mkA in either case. The electron beam was displaced on the sample surface for each scan in order to prevent the effect of surface contamination or of its surface defects when taking the spectra.
lines. The improved spectrometer resolution for detecting the chromium spectrum makes it possible to compare chromium spectra with those of other copounds. The X-ray exitation conditions were V=15 kev, I= 1.5 mkA in either case. The electron beam was displaced on the sample surface for each scan in order to prevent the effect of surface contamination or of its surface defects when taking the spectra.
The graduated graph for the determination of the fraction of the oxidized iron X=Fe3+/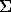 Fe in chromites was plotted by analogy with the technique desighned earlier for magnetites [4]. For this the intensities ratio in a maximum n=1 (L
Fe in chromites was plotted by analogy with the technique desighned earlier for magnetites [4]. For this the intensities ratio in a maximum n=1 (L )/1(L
)/1(L ) was used. The least squares linear approximation of the graph yields x=a+bn, where a=1.885, b=-2.840, the correlation coefficient r=-0.706, the mean square deviation sd=0.063. A collection of samples [5] where the fraction of oxidized iron x=Fe3+/
) was used. The least squares linear approximation of the graph yields x=a+bn, where a=1.885, b=-2.840, the correlation coefficient r=-0.706, the mean square deviation sd=0.063. A collection of samples [5] where the fraction of oxidized iron x=Fe3+/ Fe was defined by NGR spectroscopy were used as references. As the said method lacks the advantage of locality, to construct the correlation dependence we used the data obtained for samples with a uniform distribution of Fe and Cr.
Fe was defined by NGR spectroscopy were used as references. As the said method lacks the advantage of locality, to construct the correlation dependence we used the data obtained for samples with a uniform distribution of Fe and Cr.
# This work is supported by the Russian Foundation for Basic Research (project N 97-05-65040).
77
Taking into account the fact that publications on X-ray emission spectra of chromium in chromspinelides are scanty and that the data on the degree of oxidation of chromium can be employed in oxythermobarometry of mantle rocks, we have studied L- spectra of chromium in chromspinelides, chromium oxide and metallic chromium. The chromium spectra were resolved under the assumption that x-ray lines have the Lorentzian form.
The spectrum of metallic chromium has an unresolved doublet CrL . In chromspinelide and chromium oxide the L1,2 doublet lines are fairly resolved. The difference on the energy scale between the L1,2 doublet lines varies from 5.0 (chromspinelide) to 5.8 ev (chromium oxide) The ratio of the L
. In chromspinelide and chromium oxide the L1,2 doublet lines are fairly resolved. The difference on the energy scale between the L1,2 doublet lines varies from 5.0 (chromspinelide) to 5.8 ev (chromium oxide) The ratio of the L 1 area to the aggregate area of the L
1 area to the aggregate area of the L 1 and L
1 and L 2 components is 0.167 for chromspinelide and 0.491 for chromium oxide. Along with this, there is a displacement of the calculated and observable maxima of all the CrL
2 components is 0.167 for chromspinelide and 0.491 for chromium oxide. Along with this, there is a displacement of the calculated and observable maxima of all the CrL 1 CrL
1 CrL 2 and CrL
2 and CrL lines. In the reported data of greatest interest is the spectrum of Cr2O3, showing clear resolution of the CrL1,2 doublet that together with the fact that this compound was studied in detail by other methods, will enable one to use it as a standard. The investigation of the CrL
lines. In the reported data of greatest interest is the spectrum of Cr2O3, showing clear resolution of the CrL1,2 doublet that together with the fact that this compound was studied in detail by other methods, will enable one to use it as a standard. The investigation of the CrL ,
, spectra shows that it is possible to design a technique for the determination of the degree of oxidation of chromium in a local volume using x-ray spectral microanalysis.
spectra shows that it is possible to design a technique for the determination of the degree of oxidation of chromium in a local volume using x-ray spectral microanalysis.
So, we have studied XES of chromspinelides (Fe2+, Mg)(Cr, Al, Fe3+)2O4 on an X-ray spectral microanalyzer. We have compared them with the spectra of other iron and chromium compounds, graduated graph has been plotted by reference sample to calculate the degree of oxidation of iron in chromites. The proposed X-ray spectral microanalysis quantitative determination of the degree of oxidation of iron in chromspinelide can be of substantial support in solving petrologic problems.
References:
#Khramov D.A., Glazkova M.A., Yurakov R.M. Low temperature oxidation of ferriilmenite.
key words [ferriilmenite oxidation]
Vernadsky Institute of Geochemistry, RAS, Moscow.
Experimental modeling of the processes of rock-forming transformations of minerals under the controlled T, P, fO2 conditions makes it possible to restore the pattern of the formation and further alterations of these phases. Therefore, an investigation of the mechanism of low temperature oxidation in air of ferriilmenite (Fex3+Fe1-x2+TiO3) is a burning problem. On the other hand in the region v 0.1-0.2 ferriilmenite transits to the state of cluster spin glass at T 60K. Spin glasses belong to the class of novel promising magnetic materials. Namely, the concentration and the structural position of Fe3+ ions in ferriilmenite govern the mechanism of frustration of bounds responsible for the exchange interaction and, accordingly, transition of this oxide to the spin glass state. We report the results of a Mossbauer spectroscopic study (MS) of 57Fe nuclei and X-ray phase analysis (XPA) of the low-temperature oxidation (500oC) in air of a ferriilmenite specimen synthesized at T=1150oC in an unsealed quartz capsule. The MS and XPA data suggest that the initial specimen was single-phased with the initial ratio Fe3+/(Fe3++Fe2+) = 7.6(5)%. In order to retain the local electric neutrality Fe3+ions are likely to occupy both Ti- and Fe- containing layers in the ferriilmenite structure according to the scheme 2Fe3+=Fe2++Ti4+. After a ten-day oxidation some part of iron (6%) segregated in the form of hematite, and the concentration of Fe3+ in the ferriilmenite structure increased to 22(2)%. Importantly, that only the Fe2+ions are oxidized which have, as shown earlier [1] a 'pseudotetrahedral' oxygen coordination.
References:
# This work is supported by the Russian Foundation for Basic Research (project N 98-05-64275).
67