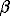key words [iron isotope fractionation]

Owing to the progress in mass-spectrometry engineering, isotope ratios for some elements like silicon [1,2], potassium [3,4] calcium[5], iron[6,7] nickel [8] and some others, have come in use in geochemical studies in the last few years. Among isotopes of such elements, the iron isotopes seem to be potentially the most important for geochemistry in view of the high abundance of iron and of its involvement in many processes taking part in the Earth crust. Nevertheless, there exist doubts that the equilibrium fractionation of the iron isotopes is significant, since notable isotopic fractionation has been observed for elements forming ionic chemical bonds [2].

To estimate the scale of the equilibrium iron isotope fractionation, a new method for evaluation of equilibrium fractionation factors is suggested. The method is valid for elements having at least one Mossbauer-sensitive element. The method is based on the previously derived equation connecting the 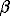-factor with the kinetic energy of the isotopic substituted atom [9-1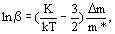1]:

(1)

where ln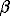 is the logarithm of the 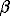-factor; K is the kinetic energy of the isotope substituted atom; m is the mass of atom; k is the Bolzmann constant; T is the temperature; superscript * marks the values referring to the isotopic form; m=m*-m.

The second-order Doppler shift in the free-recoil resonant Mössbauer frequency can be also expressed in terms of the kinetic energy [12,13]

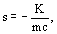(2)

where s is the second-order Doppler shift (SOD) if the free-recoil resonant Mossbauer frequency expressed in terms of the relative velocity between emitter and receiver; K is the kinetic energy of the Mossbauer-sensitive isotope nucleus; m is its mass; c is the light velocity.

A comparison of eqs(2) and (3) gives the relation between the SOD in the free-recoil resonant Mossbauer frequency and the 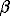-factor.

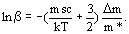(3)

In eq(3) m is the mass of the Mossbauer-sensitive isotope (for example ⁵⁷Fe).

The extent of the equilibrium iron isotope fractionation is estimated from the data on the SOD in Mossbauer spectra. The results are presented on the figure. Experimental data on SOD for ⁵⁷Fe isotope are taken from [14-19]. The measurements of the SOD in [14,19] did not aim at the estimation of the equilibrium isotope constants. As can be seen from figure the equilibrium fractionation of iron isotope exceeds the uncertainties of mass-spectrometric measurements (that is 1^o/°° [6,7] including the sample preparation procedures) up to 1000K. This opens new potentialities for using the iron isotopes in a variety of geochemical investigations.

1. Molini-Velsko C.A. (1986) Geochim. Cosmochim. Acta p.2719.
2. Li Yanhe et al (1995) Chinese Journal of Geochemistry V.14, p.213
3. Humayun M. & Clayton R. (1995) Geochim. Cosmochim. Acta V.59 p.2115.
4. Humayun M. & Clayton R. (1995b) Geochim. Cosmochim. Acta V.59 p.2131.
5. Russel W.A. et al. (1978) Geochim. Cosmochim. Acta V.42 p.1075.
6. Volkening J. & Papanastassiou D.A. (1989) V.347, p.L.43-L.46.
7. Dixon P.R. et al (1992) p.915.
8. Shukolukov A. & Lugmair G.W. Science V.259 (1993) p.1138.
9. Polyakov V.B. (1991) Zhurnal Fizicheskoy Khimii V.65 p. 1317 (in Russian).
10. Polyakov V.B. & Kharlashina (1994), V.58, p.4739-4750.
11. Polyakov V.B. & Kharlashina (1995) Geochim. Cosmochim. Acta V.59, p.2561.
12. Josephson B.D. (1960) Phys. Rev. Letters V.4, p.341
13. Pound R.V. & Rebka G.A. (1960) Jr. Phys. Rev. Letters V.4 p.274.
14. Eibschutz M., et al. (1967) Phys. Rev. V.156, p.562.
15. Housley R.M. & Hess F. (1967) Phys. Rev V.164, p.340.
16. O'Connor D.A. et al. (1972) J. Phys. F: Metal Phys. V.2, p.1179 .
17. Hazony Y. (1966) J. Chem. Phys. V.45, p.2664.
18. Reinsch L. et al. (1985) Eur. Byophys. J. V.12, p.161.
19. McCammon et al (1995) Phys. Chem. minerals, V.22, p.11.

key words [hydrogen isotopy water dunite fractionation]

Emission of hydrogen gas has been observed in various geological circumstances. With the exception of H₂ manifestations related to gas deposits and organic gases, most reports for the last two decades have been concerned with hydrogen degassing in active zones of tectonic faults [1,2] and in hyperbasites [3,4,5]. Most recognised alternatives for V.I. Vernadsky’ hypothesis of `hydrogen breath` of the planet interior are liberation of H₂ from (OH) -groups

of minerals at their self-oxidation and decomposition of water on fresh cleavages of crystals, which are experimentally confirmed [6].

The goal of this experimental; series was to obtain hydrogen under the conditions approximated to its emission in the Kempirsai chromite deposit localized in hyperbasites of the Kempersai massif in the South Urals [4]. The determination of the isotopic composition of H₂, forming in experiment, was the criterion of correlation between experimental and natural process. The experimental technique involved grinding and prolong intermixing of hyperbasite materials with water at relativly low temperatures (22 and 80^oC) for which evacuated glass reactors with controllable electric heating and magnetic rotating grinders were employed. The duration of the runs was 50 to 100 h. Preliminary degassed water, taken for the runs, had dD=-80°/°°.(SMOW). The runs were conducted in two versions: 1) with the substance preliminary ground to powder (200 mesh), denoted by asterisk in the table; 2) with 0.25-2 mm grains ground in the course of the run. The starting material was olivine (»9% fayalite): partly serpentized dunite from the Molodezhnaya mine end face wherein hydrogen was emitting , massive chromite ore from the same end face, and quartz (for the determination of the experimental background). The main results are listed in the table.

The obtained amounts of H₂ exceeded appreciably the background and were dependent both on the experimental conditions (temperature, duration) and mineral composition of the taken material and its grinding extent. H₂ forms most intensively in the case of chromite (which, apparently, explains the confinement of hydrogen gas release to ore chromite deposits). The ability of chromite to generate H₂ is by a factor of 1.5 higher than that of dunite and olivine. this suggests that for the formation of H₂ at oxidation and self-oxidation reactions the total ferruginosity of minerals is not a determining factor. The concurrent runs with ground and unground charges of the same mineral show that the supposed mechanism of H₂ formation on fresh cleavages of minerals is no less effective than oxidation. The documented isotopic composition of the experimentally obtained hydrogen reflects the ratio of the rates of its formation from water and of the isotopic exchange of H₂ with water. Lower experimental temperatures decrease the rate of the H₂ formation. This isotopic composition of hydrogen, emitting in the Kempirsai chromite deposit (dD=-766°/°° [4] has been reproduced in the runs with chromite and dunite at 22-23^oC.

Table.

1. Kitoe I., Matsuo S., Wakita H., Nakamura Y.. (1980) D/H ratios of H₂O in soil gases as an indicator of fault movements // Geochem. Jour., V.14, p.317-320.
2. Angino E.E., Coveney Jr.R.M.., Goebel E.D. (1984) Hydrogen and nitrogen-origin, distribution and abundance, as follow up. // Contrib. Mineral. Petrol. 14.
3. Neal E., Stanger G. (1983) Hydrogen generation from mantle source rocks in Oman. // Earth and Planet. Sci Lett, V.66, p.315-320.
4. Ukhanov A.V., Devirtz A.L., Ivanov N.D. (1987) Isotopically light hydrogen at Kempirsai (South Urals) // Ac. Sc. Proc., V.293, N.3, p.700-704.
5. Devirtz A.L., Gagauz F.G., Grinenko V.A., Lagutina E.P., Perevozov V.V., Shukolyukov Yu.A. (1992) On the origin of hydrogen in ultrabasic rocks of the Kempirsai massif. // Geochim., N.7, pp.1058-1064.
6. Sugaisaki R., Ido M., Takeda H. et al. Origin of hydrogen and carbon dioxide in fault gases and its relation to fault activity. // Jour. of Geol., V.91, N.3, p.239-258.