AL = AK, BL = BK (CV
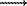 Cp), CL = Tn-2 = 1/CK2.
Cp), CL = Tn-2 = 1/CK2.Crystal growth, structure and physical
properties of crystals
Kuznetsov V.N. and Kozlov V.K. The temperature dependence of paratelluride heat capacity expressed as superposition of Lorentz distribution.
key words [paratelluride heat capacity]
The equation proposed by the authors in 1988 describes the experimental data on temperature dependences of heat capacities of crystalline substances on the basis of Lorentz distribution within the T interval from 10-30 K to phase transition point as:
Tmelt
Cp = AL[1-1/(1+CLT2)] + BLT.|(1)
Tmin
This equation asymptotically tends to:
Tmelt
Cp = AK +BKT + CK.T-2|
Tmin
that is Kelly equation, where Tmin,K>>Tmin,L˜Tmax within the area Cp = f(T3);
AL = AK, BL = BK (CV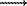 Cp), CL = Tn-2 = 1/CK2.
Cp), CL = Tn-2 = 1/CK2.
Equation (1) possesses a number of properties:
(1) lim L = 0;
T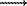 0
0
(2) in the limit: AL = AK = 3Rn;
(3) the equation has a point of inflection;
(4) B coefficient corrects the heat capacity value on transition from CV to Cp.
The curves Cp versus T for crystalline Te approximated by Lorentz (solid line) and Kelly (dashed line) equations are shown in Fig.1 (D is the Debye area, L is the area of Lorentz description, and L==K is the area of equivalent Lorentz and Kelly descriptions).
Intricate character of the temperature dependence of heat capacity of paratelluride (Fig. 2) results from the imperfect conception about crystalline state of matter. In this case, the superposition of the following three equations is required to describe properly the available experimental data:
Cp = 72.84. + 8.733 × 10.T- 1.1 × 10T-2.(300-1006 K),
Kelly approximation (error is 1.5%);
Cp =. 63.21 + 2.417 × 10-3 × T- 63.21/(1 + 7.83 × 10-5× T2)
(80-1006 K), Tn = 114.6 K,
Lorentz approximation of all available data using the least-squares method (error is 0.6%);
Cp =. 3.3 × 10-3 T + L1. (Tn,l= × 78.1K; A1 = 38.5) + L2. (Tn,2 = × 169K; A2 = 6.0) + L3 (Tn,3= × 253K; A3 = 34.1) (30-1006 K),
the superposition of Lorentz equations (error is 0.3%).
The given example demonstrates the applicability of Lorentz equation for description of crystalline state of substances.
Figure2.
# Kotel'nikov A.R., Bychkov A.M., and Koval'skii A.M. Synthesis and refinement of the unit-cell parameters of (K,Rb)-feldspar solid solutions.
key words [feldspar init-cell parameters])
# This study was supported by the Russian Basic Reseacrh Foundation, project no. 95-05-14900.
44
Potassium-rubidium feldspar solid solutions were synthesized from gel mixtures at hydrothermal conditions (T = 650-700oC, P = 1-5 kbar). The mixtures of (K,Rb)-feldspars and leucites are formed at X(Rb) > 0.5, T = 700oC, and P = 1 kbar. The stability of the feldspars increased relative to leucite with decreasing temperature to 670oC and increasing pressure to 5 kbar. According to microprobe studies, there was a good agreement between the real and theoretical feldspar compositions.
The (K,Rb)-feldspars obtained were analyzed by X-ray diffraction using a DRON-1.5 diffractometer at radiation Co-K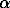 1 (
1 ( =1.78892e). Silicon of spectral purity was used as an internal standard. The unit-cell parameters were verified relying on 45 - 57 reflexes in the 2q range 15 - 85o.
=1.78892e). Silicon of spectral purity was used as an internal standard. The unit-cell parameters were verified relying on 45 - 57 reflexes in the 2q range 15 - 85o.
The unit-cell parameters depend linearly on the solid solution composition. The following equations were derived for the concentration dependences of the unit-cell parameters:
a = 8.6041 + 0.237 * X (+/- 0.0008) e
b = 13.0293 + 0.0094 * X (+/- 0.001) e
c = 7.1791 + 0.0143 * X (+/- 0.0006) e
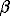 = 116.026 + 0.251 * X (+/- 0.008) eo
= 116.026 + 0.251 * X (+/- 0.008) eo
V = 723.19 + 20.33 * X (+/- 0.10) e3
From tentative evaluation, the (K,Rb)-feldspars obtained are assigned to the series sanidine - Rb-sanidine and characterized by zero excess mixing volume, which is the evidence for their ideality.
Laricheva O.O., Kalinichenko A.M., and Kozerenko S.V. Proton magnetic resonance in synthetic molybdenites.
key words [molybdenite proton magnetic resonance]
The proton magnetic resonance (PMR) in natural sulfides (pyrite, marcasite, arsenopyrite) was first observed by G.B. Bokii and A.M. Bondar' [1]. This PMR signal was attributed to the presence of hydrogen in the anionic sublattice of the sulfides.
Figure. PMR spectra.
1 - OH-, wt %; 2 - loose H2O, wt%
Table 1.
45
|
Run no |
Run duration, days |
ToC |
P, 108\Pa |
pH initial |
pH final |
S-2,mg final |
Mo, g/l |
S, mg |
OH,wt%; |
loose H2O wt %; |
|
V12 |
14 |
360 |
0.5 |
9-10 |
10 |
no |
5 |
200 |
1.1 |
1.2 |
|
V11 |
29 |
360 |
0.5 |
10-11 |
10.7 |
-220 |
5 |
200 |
1.2 |
0.6 |
|
V8 |
61 |
360 |
0.5 |
10 |
9.8-10 |
-620 |
5 |
200 |
1.1 |
0.6 |
|
V10 |
90 |
360 |
0.5 |
11 |
11.2 |
-50 |
5 |
200 |
no |
0.6 |
|
V9 |
185 |
360 |
0.5 |
10 |
9.5 |
-700 |
5 |
200 |
1.1 |
0.6 |
|
C7 |
15 |
360 |
0.5 |
11-12 |
9.8-10 |
-620 |
50 |
200 |
0.18 |
1.36 |
|
C1 |
35 |
360 |
0.5 |
10 |
10.8 |
no |
50 |
200 |
0.20 |
0.19 |
|
C2 |
80 |
360 |
0.5 |
9 |
10.8 |
no |
50 |
200 |
0.40 |
0.50 |
|
C4 |
162 |
360 |
0.5 |
10-11 |
10-11 |
no |
50 |
200 |
0.06 |
0.94 |
|
C5 |
233 |
360 |
0.5 |
10-11 |
10.7 |
no |
50 |
200 |
0.15 |
0.70 |
|
C6 |
368 |
360 |
0.5 |
10-11 |
11.4 |
no |
50 |
200 |
2.0 |
no |
They also suggested that the structural hydrogen in sulfides is responsible for their non-stoichiometry frequently observed. Later, Kalinichenko and co-authors [2] studied a great collection of natural pyrites by PMR. It was shown that the PMR signal intensity of pyrite correlates with its oxygen content. From these results, the assumption was made that the most of structural hydrogen in pyrite is present in the form of OH- groups.
Molybdenite is an appropriate object for PMR studies of sulfides because its natural counterpart often shows significantly nonstoichiometric composition.
Molybdenite crystals were synthesized under hydrothermal conditions at T=350+10oC and P=108 - 0.5108 Pa. The run duration ranged from 14 to 368 days.
The starting solutions were prepared from NH4Mo7O24 × H2O with Mo concentration 5-50 mg/l. Sulfur hydrogen was bubbled through the solution for 0.5-1.5 h until the formation of thiomolybdate, the orange-red-brown color of the solution was due to MoS42- ions. pH was maintained at 9-11 by adding concentrated ammonia. Saturation of the starting solution with sulfur hydrogen at a given pH value was a necessary condition of the experiment. A silver/silver sulfide electrode was used to control over the H2S concentration. Crystalline sulfur (200-800 mg) was added to the thiomolybdate solution.
The purity of the molybdenites obtained was verified by X-ray analyses. PMR spectra for all molybdenite samples were recorded with a RYa 2031 continuous oscillation spectrometer (vo = 16 MHz) at room temperature. The spectrum consists of two components. The minor component (figure, dashed line) ( H2 Gs) is provided by tightly bound protons.
H2 Gs) is provided by tightly bound protons.
The approximate proton contents derived from the spectra were recalculated for the equivalent OH--groups. Ca(OH)2 was used as a standard. The molybdenites with different OH- content (from 0 to 2 wt % of OH-) were obtained, i. e. the continuous series from pure molydenite to that with S2- partially substituted for OH-. In synthetic molybdenites the PMR signal ranges within wide limits because of significant amounts of structurally bound hydrogen (from 0 to 2 wt %), which is most likely to occur in the form of OH--groups.
The experimental data obtained suggest that the non-stoichiometry of natural and synthetic molybdenites may result from the substitution of S2- for OH- in the anionic sublattice of the mineral.
References:
Kiseleva I.A., Ogorodova L.P., Mel'chakova L.V., Belitskii I.A., and Fursenko B.A. Thermodynamic properties of natural pollucite.
key words [pollucite thermodynamic properties]
Pollucite is a structural analog of analcime. Substitution of sodium for cesium in the analcime structure results in loss of water. Analcime and Cs-
46
pollucite are the end members of the solid solution series Cs1-xNaxAlSi2O6 xH2O (0<x<1).
Natural pollucite from East Siberia of the composition Cs0.83Na0.17Si2O6×0.17H2O was used for thermochemical studies.
Bennington and co-authors [1] measured the enthalpy of formation of the natural pollucite of the composition
Cs0.65Na0.185Rb0.028(AlSi2)[O5.863(OH)0.137]×0.19H2O
by the HF-acid-dissolution calorimetry. Later, Semenov and co-authors [2] determined the enthalpy of formation of synthetic anhydrous Cs-pollucite (CsAlSi2O6) by high-temperature dissolution calorimetry. Correlation between these data is difficult because of great difference in composition of the pollucite samples used.
The enthalpy of pollucite dehydration was determined by the method of "repeated drop". The water loss was estimated by weighing a sample before and after the run (accuracy +2×10-3 mg). The enthalpy of formation of pollucite was obtained by high-temperature dissolution calorimetry at 973 K using the melt solvent of 2PbO×B2O3 composition. Corundum and platinum samples were used as calibration standards in dehydration and dissolution experiments, respectively.
The enthalpy of pollucite dehydration was 14.1+ 4.7 kJ/mol. The ethalpy of formation was regarded as a sum of the enthalpy of dehydration and the enthalpy of formation of dehydrtated natural pollucite. The latter was calculated on the basis of two thermochemical cycles: the reaction of pollucite formation from the appropriate oxides and the exchange reaction involving the dehydrated analcime and cesium and sodium chlorides. The enthalpies of formation of dehydrated pollucite from elements are -3050.0 +14.2 and -3050.8+13.3 kJ/mol, respectively, and are almost coinsident. The enthalpies of formation of hydrous pollucite also are in good agreement: -3112.7+15.0 and -3113.5 + 14/2 kJ/mol, respectively. These results are consistent with Bennington's data [1] obtained for the natural pollucite with similar water content (-3098.5 +3.6 kJ/mol). To adjust our data to the composition of Cs-pollucite, a correction was made for the heat of dissolution of unhydrous analcime (determined previously). The obtained enthalpy of formation of Cs-pollucite (CsAlSi2O6) is -3068.7+13.3 kJ/mol and is in good agreement with Semenov's data [2] obtained for synthetic pollucite of the same composition (-3083.4 + 5.0 kJ/mol).
References:
Evstigneev A.V., Sergeeva E.I., Devina O.A., Khodakovsky I.L. Solubility of hematite in aqueous solutions at temperatures 25-300oC and saturated vapor pressure.
key words [hematite entropy solution]
The proposed in the review Parker and Khodakovsky [1] standard values of the free energy and entropy of Fe3+ ion in an aqueous solution,  fGo =-16.23+1.1 kJ/mol, So =-278.4+7.7 J/mol·K, are based on the adopted values of the Fe2+ thermodynamic properties in aqueous solution and potential Eo Fe2+ /Fe3+ . In the present work, an attempt has been undertaken to obtain a standard entropy of the Fe3+ ion in aqueous solution using the measurement results of hematite solubility in aqueous solutions of acids [2-4].
fGo =-16.23+1.1 kJ/mol, So =-278.4+7.7 J/mol·K, are based on the adopted values of the Fe2+ thermodynamic properties in aqueous solution and potential Eo Fe2+ /Fe3+ . In the present work, an attempt has been undertaken to obtain a standard entropy of the Fe3+ ion in aqueous solution using the measurement results of hematite solubility in aqueous solutions of acids [2-4].
1/2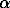 -Fe2O3(k) + 3H+(sol-sol) = Fe3+ (sol-sol) +3/2H2O
-Fe2O3(k) + 3H+(sol-sol) = Fe3+ (sol-sol) +3/2H2O
The calculation of the free formation energy (Gibbs’ energy) of an ion Fe3+ in an aqueous solution has been performed from the data of three experimental hematite solubility studies in the range of temperatures and pH of solutions: 358K in 0.12 M HCl (Berner [2]); 373, 393, 413, and 433K, 0-0.2 M HCl (Melent'ev et al [3]) and 473K, 0.01-0.32 M HClO4 [1].
The experimental results were processed as follows:
1) the equilibrium composition of the aqueous phase in the experimental systems was calculated using Mironenko's program [4] (using a method of free Gibbs energy minimization), therewith free formation energies for simple ions were assumed to be 0 [5]. It was supposed in the calculations that the following particles: H2O, H+, O2(sol), Cl-, Fe3+, FeCl2+, FeOH2+, OH- are present in the aqueous solutions.
2) the stability constants of the chloride complex FeCl2+, required for the calculation, were derived from the equation:
lgK=0.006T + 1167.136/T +3.481, (2)
obtained by us from the experimental measurements by Tagirov and Zotov in the temperature range of 25-
47
90oC [6], and the hydrolysis constants of an ion FeOH2+ from the results of the measurements by Kotova and Zotov at 25-200oC[7].
3) the calculations for this system by Shvarov’ program (GIBBS) [8] agreed satisfactorily with the results obtained by Mironenko's program.
4) the activities of Fe3+, H+ in aqueous hydrochloric solutions were calculated for each HCl concentration examined in [2] and [3], and on the base of the obtained data the equilibrium constants of the reaction (1) at I=0 (table 1) and within 358-433K were obtained.The equilibrium constant value of the reaction (2) at 473.15K and I=0 (lgK=-4.54+ 0.36) obtained in our work [1] agrees well with the results of [2,3].
Table 1. Equilibrium constants of the reaction (1) at I=0 (our calculation)
|
T K |
HCl, M |
lg Ko |
Reference |
T K |
HCl, M |
lg Ko |
Reference |
|
358.15 |
0.12 |
-2.00 |
[2] |
393.15 |
0.10 |
-3.02 |
[3] |
|
373.15 |
0.20 |
-3.39 |
[3] |
413.15 |
0.20 |
-3.32 |
-'- |
|
373.15 |
0.20 |
-3.33 |
-'- |
413.15 |
0.10 |
-3.15 |
-'- |
|
373.15 |
0.20 |
-2.84 |
-'- |
433.15 |
0.20 |
-4.18 |
-'- |
|
393.15 |
0.20 |
-3.26 |
-'- |
433.15 |
0.10 |
-4.14 |
-'- |
Using the equations of the temperature dependence of Cp for H2O (liq.), Fe3+ (sol), Fe2O3 (c) from [9,10,11], respectively, we obtained the equation for  Cp of the reaction (1) in the temperature interval from 298 to 473 K.
Cp of the reaction (1) in the temperature interval from 298 to 473 K.
 Cp=38.867 +0.30971T10-3 - 3.012105-T 2- 21937/(T-190)
Cp=38.867 +0.30971T10-3 - 3.012105-T 2- 21937/(T-190)
(3)
We have for  rS(298.15T) of the reaction (1):
rS(298.15T) of the reaction (1):
 rS(298.15T) = (
rS(298.15T) = ( rH(298.15) -
rH(298.15) -  rG(T) + ò
rG(T) + ò CopdT)/T -
CopdT)/T -
-ò ( Cop/T)dT (4)
Cop/T)dT (4)
Having calculated the enthalpy of the reaction (1) from the data of the works [11,12,13], one can calculate for each experimental values of lg K the corresponding value of  rS(298.15) (table 2).
rS(298.15) (table 2).
Table 2. Change of the entropy in the reaction (1).
|
|
Reference |
|
-210.3+6 |
Berner [2] |
|
-213.8+12 |
Ivanenko et al [3] |
|
-216.0+8 |
this work |
Using the weighted mean of  rSo(298.15)=-212.8+8 J/mol K, we obtained for Fe3+ (sol): So(298.15) =-275.0+ 8.0 J/mol K.
rSo(298.15)=-212.8+8 J/mol K, we obtained for Fe3+ (sol): So(298.15) =-275.0+ 8.0 J/mol K.
Inasmuch as from the data of the work [1]  fH(298.15)Fe3+ (sol) =- 49.0 + 1.5 kJ/mole, then
fH(298.15)Fe3+ (sol) =- 49.0 + 1.5 kJ/mole, then
 fG(298.15)Fe3+ (sol) =- 16.5 + 3.4 kJ/mole.
fG(298.15)Fe3+ (sol) =- 16.5 + 3.4 kJ/mole.
Knowing (H298.15) and (S298.15) for the reaction (1) one can obtain lgK (298.15) = 0.2+0.4.
References:
48
#
Kharlashina N.N. A model for calculating anharmionic effects in thermodynamic and spectroscopic properties of minerals.key words [anharmonic parameter microscope model]
Taking into account anharmonic effects is needed for thermodynamic calculations at high temperatures and pressures (for example, to describe exceeding Dulong and Petit limit of heat capacity). Two types of spectroscopic parameters are commonly used for mode anharmonisity:
Gruneisen parameter 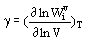 (1)
(1)
and anharmonic parameter 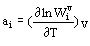 (2)
(2)
There are theoretical estimation (Sherman, 1980, 1982) and lattice dynamic calculation results (Reynard et al., 1992) for Gruneisen parameters  i , but any theoretical estimation of parameters ai have been as yet lacking. The empirical approach suggested and developed by Gillet et al. (1989-1995) consists in inserting experimental pure-temperature dependence of frequencies wi(T) into thermodynamic calculations. The approach gives qualitative results but is not well justified.
i , but any theoretical estimation of parameters ai have been as yet lacking. The empirical approach suggested and developed by Gillet et al. (1989-1995) consists in inserting experimental pure-temperature dependence of frequencies wi(T) into thermodynamic calculations. The approach gives qualitative results but is not well justified.
In this paper a simple microscope model for describing anharmonic thermodynamic and spectroscopic properties is suggested. The model is based on considering a crystal as a giant macromolecule and applying the methods of calculations developed for polyatomic molecules. If the third- and fourth-order terms are included into potential energy expansion along with the second-order terms then the energy level of a polyatomic molecule can be written as (Hezberg, 1949):
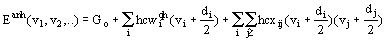 (3)
(3)
where vi is an integer quantum number of i-th mode, wiqh are zero frequencies, xii is due to own normal mode anharmonicity and xij is due to coupling between modes I. and j. The transition frequency of i-th mode is:
 (4)
(4)
The number of modes in a solid is of the order of 1023, so one can not observe the fine structure of energy levels as in molecules. Let us suppose that in a crystal the visible frequency peak wiv corresponds to the average transition frequency in thermodynamic sense. Averaging wi and differentiating with respect to temperature one can obtain
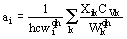 (5)
(5)
Here Cvk -heat capacity corresponding to k-th mode, xij=2xii was taken for convenience. Thus one can calculate all vibrational thermodynamic properties (free energy, vibrational energy, heat capacity, entropy) and spectroscopic anharmonic parameters ai on the base of a set of vibrational frequencies wiqh and mode interaction coefficients xik.
Application of the model is shown by the examples of: 1) some polyatomic molecules (CO2, NF3, SO3) considered as microcrystals, for which spectroscopic constants wi and xik are known, 2) several minerals (forsterite, coesite, stishovite) using model vibrational spectra and spectroscopic values of the mean ai and assuming xik/(wi wk)=const. The results for CO2 and forsterite are shown in Fig.1, where mode anharmonic parameters ai and heat capacity are presented as a function of temperature.
Conclusions:
1. The most of calculated anharmonic parameters ai are negative and have values of the order of 10-5 K-1 for molecules as well as for minerals, what is consistent with experimental spectroscopic results (Gilett et al, 1989-1995).
2. The temperature dependence of anharmonic parameters ai is evaluated.
3. Strictly speaking, the use of the dependence wi(T) overestimates anharmonic corrections to the heat capacity Cv, allowing estimation of the upper limit of the effect (see Fig.1). Anharmonic corrections for mineral heat capacity calculated by the presented method are somewhat lower than those obtained by Gilet et al (1991, 1992) and correspond well to experimental data.
# This study was supported by Russian Basic Research Foundation (95-05-14945)
49
Fig.1. Anharmonic parameters ai and heat capacity for CO2 and forsterite.
#Shapkin A.I. and Sidorov Yu.I. Mathematical analysis of microrhythmic chemical zoning of olivine grains from the Divnoe meteorite.
key words [olivine meteorite zoning]
The variation of fayalite content in olivine grains of the Divnoe meteorite was previously studied by microprobe analysis [1]. The microphotographs of a thin section of one olivine grain and the diagram of spatial variation of fayalite content presented in this work testify that the clear rhythmic variation of fayalite content within the range 22-25 mol % occurs over a length of 60  . The noted rhythmic chemical zoning has a period of the order of a few micrometers and is explained by the authors [1] as a result of decomposition of olivine solid solution.
. The noted rhythmic chemical zoning has a period of the order of a few micrometers and is explained by the authors [1] as a result of decomposition of olivine solid solution.
Within the present study, determination of other frequencies of the chemical rhythm by harmonic analysis methods was attempted on the basis of data [1].
As a result of reduction of the analytical data to the spatial forsterite distribution (Fig. 1), the systematic component of the function of Mg/Fe distribution in the grain bulk was derived using the linear regression method. The linear approximation of the function component gives 76.618 - 0.0122L, where L is the distance from the grain surface (in micrometers). Thus, the slope of the forsterite concentration trend is 0.0122 mol %  , that is the average Mg/Fe ratio
, that is the average Mg/Fe ratio
# The authors thank M.I. Petaev for remarks and discussion of this work. The present study was supported in part by the Russian Basic Research Foundation, project no. 94-05-16405.
50
decreases towards the grain core (3.27 at the surface and 3.15 at a depth of 60  ).
).
After subtraction of the obtained linear trend from the distribution function (Fig. 2), the following algorithm was employed to determine the main frequencies of the distribution.
1. The high-frequency component of the distribution function was filtered off by the moving-average method. The period of the component proved to be equal 3  , which correlates well with [1] data. The post-filtration distribution is shown in Fig. 3 (dashed line).
, which correlates well with [1] data. The post-filtration distribution is shown in Fig. 3 (dashed line).
2. A number of harmonic characteristics of the distribution function, such as i (harmonic number), wi (harmonic frequency), ai and bi (amplitude coefficients), and li (harmonic period in  ), were derived using the method of determination of unknown periodic components of a f(xi) function assigned at N equidistant points [2]. This method is based on solution of an equation of the type
), were derived using the method of determination of unknown periodic components of a f(xi) function assigned at N equidistant points [2]. This method is based on solution of an equation of the type
cos mw - 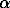 I cos (m-1)w - ... - 0.5w
I cos (m-1)w - ... - 0.5w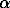 m=0,
m=0,
where m is the number of harmonics determined and 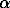 i are the coefficients fitting the linear equation system
i are the coefficients fitting the linear equation system
m-1
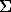 (fi+k-1+f2m+i-k-1)
(fi+k-1+f2m+i-k-1)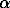 k+ fm+i-1
k+ fm+i-1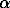 m- fi-1 - f2m+i-1=0, i=1..N-2m
m- fi-1 - f2m+i-1=0, i=1..N-2m
k=0
F(x) = 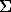
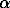 I cos (wi(x-11)) + bi sin(wi(x-11))
I cos (wi(x-11)) + bi sin(wi(x-11))
The plot of F(x) function is shown in Fig.3.
In summary, there are reasons to conclude that the function of Mg/Fe distribution in olivine grains has the three more periods and the systematic linear trend in addition to the period noted by the authors [1]. The obtained results can not be interpreted on the basis of solid solution decomposition mechanism.
|
Figure 1. |
Figure 2. |
Figure 3. |
|
i |
w |
ai |
bi |
li, |
|
1 |
.1352 |
.3616 |
- |
46.5 |
|
2 |
.4184 |
-.1451 |
-.1840 |
15. |
|
3 |
.6524 |
-.1638 |
- |
9.7 |
References :
51