| Journal of Petrology | Pages |
© 1998 Oxford University Press |
The textures of plutonic rocks are one of their most striking aspects, but they have been little used to elucidate petrological processes as compared with chemical and isotopic methods. Where used, discussion has tended to be qualitative, in contrast to quantitative chemical methods, hence reducing the weight of this approach. Indeed, it is not possible to verify physical models if quantitative data are not available. Quantitative textural studies of volcanic rocks are becoming more common and these methods are applied here to the development of anorthosite. Quantitative textural studies of plutonic rocks really started with Jackson's studies of the Stillwater complex in 1961 (Jackson, 1961). He measured crystal size distributions, but did not record the area that he measured, hence his data cannot be completely compared with modern data. His pioneering work was not really followed up, and since then most studies have looked only at `average' or `typical' crystal sizes. These data are much less revealing of petrological processes than crystal size distributions, partly because they only give one parameter for each sample. The few existing studies of crystal size distributions in plutonic rocks have not treatedplagioclase. One problem especially pertinent to quantitative textural studies is the way that many igneous petrologists look at rocks: they commonly try to reconstruct how a rock has formed by examining the final, fully crystallized product [for a recent example applied to anorthosite, see
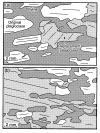
Lafrance et al., (1995)]. However, most plutonic rocks probably form by both growth and solution of crystals, hence many aspects of their early history are not evident in the final rock (Boudreau, 1987; Hunter, 1996; Higgins, 1997). Clearly, these processes can only be fully understood by the quantitative analysis of a sequence of textures. Realistic sequences of textural development from nucleation to complete solidification probably cannot be produced in the laboratory, although some aqueous systems may be relevant (Means & Park, 1994). Therefore, we must seek out natural sequences of textural development. Some oikocrystic plutonic rocks preserve such time sequences: early textures of chadocrysts are seen in oikocrysts, whereas the matrix material between the oikocrysts preserves the later textures (Mathison, 1987; Higgins, 1991, 1997; McBirney & Hunter, 1995). The process is as follows. Oikocrysts grew from the same magma as the chadocrysts but faster, displacing the magma between the crystals. Without a liquid to facilitate chemical transport, grain boundaries of the chadocrysts move slowly and further textural development is inhibited. Hence, textures of chadocrysts in oikocrysts or parts of oikocrysts that grew at different times can preserve a time-sequence of textural development, or at least some aspects of it. Quantitative analysis of the sequence of textures will be applied here to study the origin of anorthosite. The Lac-St-Jean anorthosite complex (LSJAC) is a massif-type body comprising many plutons, which were emplaced from 1157 to 1142 Ma into the central part of the Grenville Province, Canada (Higgins & van Breemen, 1992). Individual plutons vary widely in their degree of deformation, but in every case so far examined geochronological evidence has shown that most of the deformation was synchronous with emplacement. Similarly, metamorphic effects in the LSJAC, such as coronas around mafic minerals and baddeleyite, were produced by heat from later injections of magma, and are hence evidence of contact metamorphism (Higgins & van Breemen, 1992). Thus the LSJAC lacks regionally imposed Grenville metamorphism and deformation, although it must have cooled relatively slowly. Other massif-type anorthosites that have not been subjected to regional metamorphism or deformation show a similar degree of deformation, which is also ascribed to movements associated with emplacement of the pluton and adjacent plutons (Laramie, Wyoming, Lafrance et al., 1995; Nain, Labrador, B. Ryan, personal communication, 1997;Rogaland, Norway, Maijer & Padget, 1989). The rocks examined here are part of an early (1157 Ma) layered troctolite-anorthosite pluton of the LSJAC, centred on the town of Alma (Woussen et al., 1988; Higgins & van Breemen, 1992). The composition of the rocks and the style of the layering are variable, both on a kilometre and an outcrop scale. The samples were taken from a large, texturally variable outcrop of troctolite and anorthosite located at UTM coordinates 19U 306200 5386400, 5 km NNE of the town of Alma. The dominant texture is `Nodular' troctolite, in which amoeboid olivine oikocrysts 10-20 cm in diameter are spaced 20-30 cm apart within a matrix of anorthosite (Woussen et al., 1988; Figs 1 and 2). The oikocrysts consist of a single or possibly a few olivine crystals with abundant chadocrysts of plagioclase. The rest of the rock is dominated by plagioclase, which is commonly massive but locally foliated. Where foliated the fabric is well developed in the oikocrysts and its orientation is the same in adjacent oikocrysts (Fig. 2). The fabric is defined by the shape-preferred orientations of the plagioclase crystals. As most plagioclase crystals are flattened parallel to the albite twin plane the foliation is also defined by the lattice orientations. The foliation is also evident in the plagioclase of the matrix between the oikocrysts, but it is less well developed, although again broadly parallel to that in the oikocrysts. Here the foliation is more defined by the lattice orientations, as revealed by the orientation of the trace of the albite twin lamellae. The direction of lamination in the matrix does not wrap around the oikocrysts, as has been observed in other troctolites (compare Sept Iles Intrusion, Higgins, 1991). Figure
Figure
Elsewhere on this outcrop other textures are present. The Nodular Troctolite is transitional to fine-scale layering (Fig. 1): the oikocrysts become flatter, smaller and more numerous until they are comparable in size with the plagioclase crystals. Layers repeat at 3-10 cm intervals. Both plagioclase and olivine are similar in size to the plagioclase of the Nodular Troctolite matrix. The plagioclase is not laminated. Both types of troctolite are abruptly transitional to pure anorthosite. The troctolite-anorthosite contacts cut across layering in broad sinuous curves. The pure anorthosite resembles the matrix of the Nodular Troctolite and the anorthosite layers of the layered troctolite. The plagioclase does not have a significant lamination. Megacrysts of plagioclase and Al-orthopyroxene that are so characteristic of massif-type anorthosite complexes also occur throughout the outcrop. Oikocrystic textures similar to that of the Nodular Troctolite are commonly thought to imply a very low nucleation density of the oikocryst phase, here olivine. However, if this texture was produced by nucleation in a uniform medium at very low undercoolings then a random distribution of oikocrysts would be expected, which is not observed. It will be shown later that the plagioclase crystals have been coarsened and hence it is possible that the oikocrysts were coarsened also. Such a process can develop periodic patterns with layers (Boudreau, 1987) or more complex distributions (Ortoleva, 1994). Most of the textures described here are difficult to interpret as only the final stage is preserved. However, for the Nodular Troctolite the oikocrysts have preserved a record of textural development. The rest of this paper will be devoted to quantitative textural examination of the development of this rock. A laminated part of the Nodular Troctolite has been chosen as this further constrains the development of the texture (Fig. 3). Figure
The Nodular Troctolite is composed only of the two essential minerals, olivine and plagioclase. Olivine is only present as oikocrysts. It is not deformed or extensively altered, but near the edges of the oikocrysts it may have narrow rims of orthopyroxene. The olivine is unzoned, with 20 microprobe analyses in the range Fo 69 ± 2%, which is close to the analytical error at 95% confidence. Plagioclase crystals within the oikocrysts and the matrix have strikingly different shapes, sizes and orientations. However, more than 200 microprobe analyses of plagioclase compositions indicate that there is no systematic compositional difference between the cores of those crystals in the oikocryst and in the matrix, with 90% of analyses falling in the range 62 ± 4 % An. The analytical error was estimated to be 2% at the 95% confidence level. Plagioclase crystals in the oikocryst are euhedral to subhedral and are undeformed, displaying only albitetwins (Fig. 4a). Plagioclase crystals are larger in areas of the oikocryst with a higher proportion of plagioclase (Fig. 4b). Most crystals are unzoned. Most plagioclase crystals are well aligned in the oikocryst. Figure
In a few crystals near the edge of the oikocryst plagioclase occupies a space within the olivine that has the shape of a euhedral crystal of plagioclase, but the traces of the albite twin lamellae are oblique to the edge (Fig. 5a, b). There is no compositional difference between these new crystals and the others in the oikocryst. This morphology indicates that the original plagioclase crystal has been replaced by a new crystal with a different orientation. These crystals probably grew in from the matrix outside the oikocryst. Figure
Plagioclase in the matrix is coarse grained and laminated, but the quality of the lamination is not as good as that of the plagioclase crystals in the oikocrysts (Fig. 3a). Plagioclase crystals are generally unzoned, except for sporadic, narrow reversely zoned rims. Similar rims have been found in anorthosites of the Kiglapait intrusion, Nain, and in massif-type anorthosites elsewhere (Morse & Nolan, 1985). A number of origins have been put forward, including the proposal by
Morse & Nolan, (1985) that they formed by crystallization of late trapped liquids, enriched in calcic components rejected by earlier plagioclase crystallization. Hence their presence here indicates a lack of major grain-boundary movement in the sub-solidus state. A slightly modified explanation will be suggested later. The origin of the lamination must now be discussed, even though it is not the focus of this paper, as it may have implications for the development of other aspects of the texture to be quantified later. Higgins, (1991) and others have shown that flow of a crystal-liquid is a very efficient way to produce a well-developed foliation-compaction cannot produce significant foliation unless accompanied by very extensive recrystallization (Meurer, in preparation). The lack of wrapping of the foliation around the oikocrysts indicates that compaction, if it occurred, must have been very early. Higgins considers that the foliation was dominantly produced by flow, as it is the more efficient mechanism, but early compaction cannot be ruled out. Plagioclase crystals in the matrix are commonly slightly deformed, with pericline and albite twins, and some edges are finely granulated, giving a protoclastic texture. The absence of granulation in the oikocrysts, even atplagioclase-plagioclase contacts, shows that deformation followed crystallization of the oikocrysts, and hence occurred after the processes to be discussed here. It was probably produced by late settling or movements of the intrusion or the emplacement of adjacent intrusions. Some plagioclase crystals in the oikocrysts are slightly deformed and the olivine oikocrysts have started to develop sub-grains, indicating that the oikocrysts were not totally immune to the late deformation observed in the matrix. Three large thin sections were cut in a line from the centre of an oikocryst into the adjacent matrix for textural analysis (Figs 3 and 6). Photographs of the sections were enlarged to 30 cm * 45 cm and the outline of each plagioclase crystal in the photograph was traced by hand onto a digitizing tablet, after verifying the actual outline in the thin section with a polarizing microscope. All crystals in the thin section of the oikocryst were measured, as none were smaller than the minimum size that could be recognized in the photograph (0·25 mm). In the matrix, crystals smaller than 0·5 mm that lie along the grain boundaries of the larger crystals were interpreted to have been produced by cataclasis and were not measured. The raw positional data from the digitizing tablet were reduced to morphometric parameters using a program written by the author, and the reduced data were analysed with a spreadsheet program. Figure
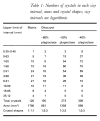
The raw data on crystal sizes are only a measurement of intersections of crystals with a plane (Table 1). Clearly, 3D size data are required for discussion. The stereological problem of conversion of 2D data to three dimensions is not simple for objects more geometrically complex than a sphere, and space does not allow it to be discussed in detail here [see, e.g. the review by
Royet, (1991)]. However, three aspects of the problem are relevant here. Table 1. Numbers of crystals in each size interval, areas and crystal shapes; size intervals are logarithmic.
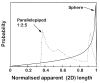
(1) For a monodisperse population (one 3D size) of identical shapes the most common 2D long axis is less than the true 3D long axis (Fig. 7). This is known as the cut section effect (Royet, 1991). There have been a number of studies of this problem for various geometrical shapes, but the shape most relevant for the case of plagioclase is the rectangular parallelepiped. Higgins, (1994) showed that for randomly distributed crystal orientations (massive texture) the most likely intersection is the intermediate dimension. That is, for a crystal 1 mm * 2 mm * 10 mm it is 2 mm. The same argument can also be applied to polydisperse populations (many 3D sizes). This effect can be compensated for if the length axis of crystal size diagrams is considered to be the length of the intermediate axis. It can, of course, be readily converted to the true length if the crystal shape is known. Crystal shapes can be measured using separated crystals or estimated from distributions of intersection width/length ratios (Higgins, 1994). Figure
(2) For a polydisperse distribution smaller crystals are less likely to be intersected by a plane than larger crystals. This is known as the intersection probability effect. Again, the problem is easily resolved for a monodisperse collection of spheres (Royet, 1991):
where nV is the total number of spheres per unit volume, nA is the total number per unit area and D is the diameter of the spheres. This relationship can be modified so that it applies to polydisperse collections of other shapes (Higgins, 1994; Peterson, 1996). However, another conversion is dimensionally also possible:
where nV(L12) is the total number of crystals per unit volume in the length interval L1 to L2 (the population density), and nA(L12) is the total number of crystals per unit area in the length interval L1 to L2. This equation is the simplest way to convert the dimensions of nA(L12), L-2, to those of nV(L12), L-3. This conversion is much more commonly applied than equation (1) and will be used here for consistency [see review by
Cashman, (1990)]. The different equations give slightly different shapes to the CSDs, but affect all CSDs similarly. (3) Intersection lengths (2D) in a monodisperse population cover a broad range about the modal length, with a maximum equal to the greatest 3D length. This is another aspect of the cut section effect. Therefore, for a polydisperse population the 3D distribution of lengths can only be found by applying the function for a monodisperse population of the same shape to the 2D length distribution. Unfortunately, the form of this function is known analytically only for spheres; shapes such as parallelepipeds must be derived numerically and can be very complex with several modes (Fig. 7; Higgins, 1994). There have been many attempts to resolve this problem (Royet, 1991). Some workers have used the shape distribution function directly, either for spheres (e.g. Armienti et al., 1994) or for more complex shapes. This method works well for spheres and near-equant objects because the modal 2D length lies close to the maximum 3D length (Fig. 7). However, it fails for complex objects because the largest 2D intersections are not very common [see point (1) above]. That is, the modal 2D length is much less than the maximum 2D length. Hence, the less abundant, and less accurately determined, larger intersections are used to correct for the most abundant intersections, introducing large errors in the corrected 3D length distributions. If the modal length, rather than the greatest length, is used then the correction is much less important and can be neglected to a first approximation. Some workers have used an empirical approach that solves all three problems. Known 3D distributions have been sampled in two dimensions and the relationship between the two numerically modelled. Some success has been achieved for CSDs that have a logarithmic-linear 3D crystal size distribution (Peterson, 1996), but the method cannot be generally applied to non-linear distributions such as those seen here without introducing unacceptable errors (see later). Equation (2) will be used here to convert the data to 3D number densities. The length in this equation is the intermediate dimension of the crystals. It should be noted that other workers use different conversions. Remembering this, and the possibilities of advances in the solution of these problems in the future, the raw 2D data are presented in Table 1, together with the areas and crystal shapes, so that the data can be readily recalculated. Population densities were plotted on a ln (population density) vs length diagram (Fig. 8) following
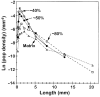
Marsh, (1988). Logarithmic length intervals were used such that each size interval is 100·2 larger than the previous bin. Each bin used in the discussion contains at least one crystal and there are no gaps with empty bins. The principal source of error at each point in this diagram is the counting statistics. All bins between 0·4 and 10 mm have significant numbers of crystals and hence errors are small on the logarithmic scale of population density. Outside these limits precision is worse, but still does not invalidate the data. To facilitate discussion of the data, the section of the oikocryst was divided visually into areas with different proportions of plagioclase-40, 50 and 80% (Fig. 8; Table 1). There values were chosen empirically to give useful sub-populations of crystals. Figure
The CSDs of each area of the oikocryst and of the matrix are all convex upwards, and the shape and position of the curve vary systematically with solidification. The position of the maximum of the CSD increases from 0·7 mm in the 40% plagioclase area to 2·0 mm in the matrix (Table 2; Fig. 8). It should be noted that the cut-off for small crystals in the matrix (see above) was 0·5 mm, considerably smaller than the observed maximum, 2 mm, hence the convex-upwards shape of the matrix CSD is not an artefact of measurement. This effect is not a consideration for the oikocryst CSDs as all crystals in the thin section were measured. Table 2. Crystal size distribution parameters.
There are not sufficient data to the left of the CSD maximum to determine if this section is linear, but overall steepness decreases with increasing solidification within the oikocryst. The matrix appears to continue this trend, but less precisely and with the same caveat as above. The parts of the CSDs to the right are broadly linear, considering the errors associated with the population density of the largest crystals. The intercept and slope of a regression of these data both decrease with increasing solidification (Table 2; Fig. 8). The overall effect for the three areas of the oikocryst is rotation of the line around a point at 4 mm.
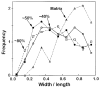
Higgins, (1994) has shown that crystal shapes can be estimated from the distributions of width/length ratios of crystal outlines. The width/length distributions of plagioclase from all three areas of the oikocryst are similar, with a mode at about 0·35 and a skewness ((mean - mode)/standard deviation) of 0·82 (Fig. 9). These values indicate an overall aspect ratio for the crystals of 1:3:3 (Higgins, 1994). The width/length distribution of the matrix plagioclase is very different: the mode of 0·8 and skewness of -0·76 indicate almost equant crystals, but it is impossible to give exact dimensions (Higgins, 1994). Figure
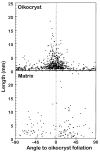
The orientation of the plagioclase crystals is defined by the trace of the albite twin planes. For most crystals the long axis in sections is parallel to the albite twin planes, hence both lattice-preferred orientations and shape-preferred orientations are identical. Within the oikocryst large plagioclase crystals are confined to a narrow range of orientations (Fig. 10), but crystals <2 mm long are more widely distributed, although still with a concentration around 0°. The plagioclase in the matrix is not nearly so well aligned (Fig. 10). The larger crystals have a mean orientation near 45°, reflecting undulations of the foliation direction visible in the outcrop (Figs 2 and 3). Crystals smaller than 7 mm are almost randomly oriented. Figure
The most important assumption of this study is that the shapes of the plagioclase crystals are not significantly modified after they have been engulfed by the olivine oikocrysts. A further assumption is that the amount of plagioclase in a given volume increases at the same time as the oikocrysts grow, or at the very least does not decrease. These ideas seem reasonable and, as indicated in the Introduction, have been adopted by other researchers. Hence, the parts of the oikocryst that contain 40% plagioclase represent the texture when the system was 40% solidified, and will now be referred to in that way. The continuity of the lamination direction between the different oikocrysts can only be explained if the material between the oikocrysts (i.e. matrix) initially had a texture similar to that within the oikocrysts. This can be generalized to indicate that all the textures developed sequentially, in order of solidification (percentage plagioclase). For example, the matrix textures (100% solidified) passed through the 40, 50 and 80% solidification textures. The simplest possible analysis of the textures, based only on crystal number density (number of crystals/volume) indicates that textural development can be divided into two periods (Table 1). The first was one of production of crystals by nucleation and growth, and hence increasing crystal number density. It was complete before 40% solidification, which is the earliest recorded texture. It is roughly equivalent to the primary textural development period of
Hunter, (1996). The second phase was of reduction in the crystal number density, but with a concurrent increase in mean grain size, resulting in an overall increase in the proportion of plagioclase until the rock was completely solidified. This process is termed textural coarsening, Ostwald ripening (Voorhees, 1992), crystal ageing (Boudreau, 1995) or competitive particle growth (Ortoleva, 1994). This phase is equivalent to the secondary textural development period of
Hunter, (1996). Obviously, the crystallization of a magmatic rock must start with nucleation and growth of crystals. Marsh, (1988) has applied CSD theory developed for industrial processes to petrology and has shown that on a graph of ln [nV(L)] vs L straight CSDs can be expected for both open-system and closed-system (batch) crystallization. For a closed system the logarithmic-linear correlation is produced by exponentially increasing nucleation with time, as would be produced if the undercooling of the magma was increasing linearly (Fig. 11a). For such relatively small undercoolings the maximum growth rate is rather high, although difficult to quantify. In batch crystallization crystal size can be correlated with crystal age, although the relationship is only linear if the growth rate is constant. Therefore, in a CSD diagram nucleation density is proxied by population density and time is proxied by length. Figure
At 40% solidification the CSD is linear, except for small crystal sizes (see later), implying that crystallization occurred in an environment of linearly increasing undercooling (Figs 8 and 11a) In this part of the section both medium-sized and large crystals are well aligned (Figs 3 and 10), hence the magma must have been sheared or flowed as a slurry during crystallization, as compaction cannot produce such a pronounced lamination (Higgins, 1991). Crystallization produces latent heat, which must be removed if the undercooling is to increase. Nucleation and growth in a flowing or circulating magma provide a mechanism to remove such heat. The more dispersed orientations of the smaller crystals indicated that flow may have ceased towards the end of this period (Fig. 10). The smallest grains are deficient as compared with a linear regression of the rest of the CSD data (Fig. 8). This could be due to a reduction of the nucleation density during the last stages of crystallization or resorption of the smallest grains after their growth (see discussion of coarsening later). If the shapes of the CSDs of the 40, 50 and 80% solidified areas are extrapolated visually then it appears that the turn-down began at about 25% solidification. Therefore, the first phase of nucleation and growth with increasing undercooling must have finished by that point. If the turn-down in the 40% solidified CSD is due to decreasing nucleation density, then this time must be one of transition to the coarsening phase, during which there was no nucleation. Otherwise the turn-down is simply the initial stage of coarsening. It is not possible to determine if there was any significant compaction during this phase for the following reasons: there was sufficient magma present that crystals could move freely and hence none were bent; there were no solid objects around which the plagioclase foliation could be bent (compare Sept Iles intrusion; Higgins, 1991); and any foliation produced by compaction would have been swamped by that produced by flow. Polydisperse multiphase mixtures are not in their lowest energy state, because of excess interfacial energy. In such systems the mean grain size tends to increase so as to reduce the overall energy of the system [see review by
Voorhees, (1992)]. Grain size can only be reduced if energy is added, by deformation for example. Clearly, there can be no nucleation of new crystals of the phase that is coarsening during this process, although other phases could nucleate and grow. Material is transferred from grains smaller than a critical radius by diffusion to the larger grains by several different mechanisms [see review by
Hunter, (1996)]. If there is no magma present then diffusion may be within the body of the grains or, more likely, along grain boundaries. If a magma is present then diffusion in the magma dominates any within-grain diffusion. Reversed rims on some plagioclase crystals imply that magma was present, at least between some grains, during the production of the textures observed here (except the final granulation). Such rims also indicate that there have not been any major grain-boundary movements in the sub-solidus. Although the thermodynamic driving forces of the process are well known and understood, the kinetics are complex and the subject of much research, especially in the field of material sciences (Voorhees, 1992). Unfortunately, the number of variables is very large and most of the systems investigated are not appropriate to geological conditions. Nevertheless, a good starting point is the earliest and most well-known solution, that formulated by
Lifshitz & Slyozov, (1961) and others, known as the Lifshitz-Slyozov-Wagner (LSW) theory. The solution is for dilute systems; that is, there is assumed to be no interaction between crystals-all communicate directly with a uniform fluid. The crystals are assumed to be spherical. Most applications of LSW theory (and modifications of the theory) have been concerned with the relationship between mean crystal size and time. However, in plutonic rocks solidification time is not well constrained. In these circumstances, an equation relating growth rate to crystal size is more interesting (Lifshitz & Slyozov, 1961):
where dr/dt is the growth rate, r* is the critical radius, r is the crystal radius and k is a rate constant. A graph of growth rate vs radius shows that crystals below the critical radius are strongly resorbed and their material is transferred to crystals slightly larger that the critical radius (Fig. 12). The growth rate of infinitely large crystals is zero. The rate constant k is dependent on temperature and its value is not known for plagioclase in this system. Figure
The LSW equation for coarsening has been modelled numerically with a spreadsheet program. Eight thousand random numbers were manipulated mathematically so that their CSD resembled that of the 40% solidified texture, except that the CSD was linear to zero length. The modelling was done sequentially on this population. Time was non-dimensionalized with steps of 0·25, 0·5, 0·75 and 1·00. The constant k and the critical radii for each step were varied to try to achieve the best fit to the natural data. Figure 13a shows the results of this model. Clearly, it is easy to produce depletion of small crystals although not as strong as is observed. However, the slope of the right part of the CSD diagram does not decrease, as is observed in the rocks, but even increases a little. Increasing the value of k merely exacerbates this problem. Figure
The limitations of the LSW equation are well known, hence it is not surprising that it is unable to model the observed CSDs. Numerous modifications have been proposed, such as extensions to high volume fractions [see review by
Voorhees, (1992)]. However, as
DeHoff, (1991) has pointed out: `The literature abounds with theoretical treatments of coarsening for an additional important reason: the existing theories do not work.' DeHoff proposed a new theory, which he called the communicating neighbours (CN) theory. CN theory is based on the observation that in many laboratory studies the growth rate of each crystal is not solely controlled by its size, but appears to be characteristic of each crystal, an effect called growth rate dispersion. This suggests that the position of each crystal is important during growth and hence that crystals communicate with each other and not only with some uniform fluid. Of course, the mechanism for communication, as in the LSW theory, is by diffusion. DeHoff, (1991) has formulated a geometrically general theory using this principle. The most readily applicable equation relates growth rate and crystal radius:
where dr/dt is the growth rate, k is a rate constant (different from that in the LSW theory), is the harmonic mean of the intercrystal distance, r* is the critical radius and r is the crystal radius. This equation illustrates the fundamental difference between the LSW and CN theories: in the former the diffusion length scale is a property of the particle itself, hence the 1/r dependence, whereas in the CN theory it is dependent on the distances to the neighbouring particles. This equation is for crystal growth controlled by diffusion. A similar equation also applies to interface-controlled growth (DeHoff, 1984). A graph of growth rate vs radius for the CN equation shows that crystals below the critical radius are resorbed rapidly, although less so than with the LSW equation (Fig. 12). The major difference is for crystals larger than the critical radius, where the growth rate increases asymptotically with radius. This equation is much more interesting than the LSW equation, as the growth rate is constant for crystals much larger than the critical radius, and will then depend on undercooling, amongst other factors (Fig. 12). The harmonic mean may be evaluated using
where [alpha] depends on the nature of the distribution and has a value of 2·18 for a Poisson distribution. The population density (nV) observed here varies by a factor of four, translating to a variation in of only 1·6. Therefore, this variable can be combined with the rate constant k into a new constant k'. Sequential modelling similar to that used for the LSW equation was applied to the CN equation (Fig. 13b). Again, the critical radius and modified rate constant (k€) were varied to achieve the best fit to the natural data. Although the smallest crystals are again depleted and the peaks of the CSDs better match the natural values, the turn-downs at small lengths are not as steep as observed. However, the match for the right side of the CSD diagram is much better: the slopes of the CSDs decrease and rotate about a point near 4 mm. It should be noted that the common practice of plotting linearly crystal population densities against length conceals the variations in the number of large crystals (e.g. Cashman & Ferry, 1988). Hence, the difference between the CN and LSW theories is not so clear on these diagrams. These models indicate that plagioclase textures developed by textural coarsening, following the CN theory (DeHoff, 1991), but why did it occur? The first stage of solidification was one of increasing undercooling (Fig. 11). However, the increasing crystallinity (of both plagioclase and olivine) would have impeded the flow of interstitial magma. Latent heat could not be removed so easily, leading to a rise in temperature (lower undercooling) and suppression of nucleation (Fig. 11). Closer to the liquidus temperature of plagioclase the critical radius increased, hence allowing coarsening to occur by the destruction of small crystals and the growth of larger crystals. The large size of the oikocrysts and the lack of smaller olivine crystals imply that olivine was also coarsened like plagioclase. Hence, it is proposed that the low population density of the oikocrysts is not a primary feature, but one developed during textural coarsening. The original population density of the olivine before coarsening may have been similar to that of the plagioclase, but is now inaccessible. Other textures in the rocks near the Nodular Troctolite support the idea that locally olivine crystals smaller than a critical size may have been dissolved. The abrupt termination of the layered troctolite against the anorthosite is most easily explained by the solution of olivine, converting troctolite to anorthosite. Perhaps late circulating magmatic fluids were focused into these areas by locally higher permeability and the olivine of the troctolite, which was smaller than the critical size, dissolved in the magma. The olivine component of the magma could have re-entered the magma chamber or been precipitated to enlarge the oikocrysts. Similar discordant bodies have been observed in other layered mafic intrusions (e.g. McBirney & Hunter, 1995; Meurer et al., 1997) and are generally considered to be the result of metasomatic processes. However, the grain size in many of these bodies is greater than that of their host rocks, hence textural coarsening may well be important. If the crystals in the metasomatic protolith are smaller than the critical size for the percolating magma, then they will dissolve, even if the chemical composition of the magma is not different from that which the crystals originally crystallized from. Hence, it may not always be necessary to propose magmatic fluids with different compositions to effect the observed changes in modal composition. Coarsening can also provide a new explanation for the origin of the poikilitic texture. The classical theory proposes that the chadocryst phase nucleated and grew first. Subsequently, the oikocryst phase nucleated, grew faster than the chadocryst crystals and engulfed them. However, there is a problem that under plutonic conditions olivine or pyroxene commonly nucleates at higher temperatures than plagioclase. This is indicated by the common occurrence of olivine-rich cumulates at the base of layered intrusions. Let us assume, for the moment, that olivine did indeed nucleate and grow first (Fig. 12). As cooling proceeded plagioclase joined olivine and the two continued to nucleate and grow together. The texture at this point would consist of olivine crystals, some partly enclosed by plagioclase. Once coarsening started the texture changed dramatically. As mentioned above, once crystallinity interferes with magma circulation latent heat cannot be removed fast enough and the temperature will rise. The temperature will be buffered close to the liquidus temperature of plagioclase as solution of plagioclase will adsorb heat. However, at this temperature olivine is more undercooled than the plagioclase and will have a higher maximum growth rate (Fig. 11). The olivine crystals will coarsen and grow rapidly, engulfing the plagioclase. Evidence of the early crystallization of olivine may only be preserved at the centre of some oikocrysts, which are not volumetrically important, and hence will only be rarely seen. Hence, coarsening necessarily produces an apparent crystallization order that is the reverse of the order of nucleation of the phases. This process is not at odds with the original assumption of this study-that oikocrysts preserve the early textures of the chadocryst phases-as the coarsening of the olivine starts early in the solidification of the rock.
Means & Park, (1994) have suggested that a number of textural processes that they observed in polyphase artificial systems might be applicable to igneous rocks. In particular, they found evidence for phase boundary migration that has changed the apparent order of crystallization. In this study the textural evidence indicates that the phase boundaries are resistant to change, as illustrated by the preservation of euhedral `holes' in the oikocryst now occupied by new plagioclase crystals (Fig. 5). Hence, this aspect of their model is not applicable here. However, grain boundary migration, as they also observed, is clearly very important here. One particularly striking aspect of the textural development is the loss of quality of lamination and change of crystal shape in the last developed textures (i.e. the matrix). This can be readily explained by the coarsening process in two ways. As the proportion of magma decreases the mechanism for diffusion must change also (Hunter, 1996). Initially, diffusion is mediated via the magma, but later diffusion must be partly restricted to grain boundaries, as within-grain diffusion will be slower still. Such a change in diffusive mechanism may affect the growth of different faces of the particle by changing the width of the chemical boundary layer. Another explanation is based solely on mechanical processes, as follows. As grains grow at the expense of their smaller neighbours their ends will meet neighbouring crystals before the sides. Hence growth on the sides will be less restricted and the grain will become more equant. There will also be rotation of individual crystals to accommodate better their new dimensions. This effect is particularly important when space is limited, for example, during the last stages of solidification. This process will steadily reduce the quality of the lamination, as there is no counteracting force, such as the original magmatic flow, to restore the original quality of lamination. Similar grain rotation has been observed in the experiments of
Means & Park, (1994). Finally, textural coarsening may provide another explanation for the origin of reversely zoned rims on plagioclase. The cores of most plagioclase crystals are more An rich than the rims (normal zoning). Hence, as crystals smaller than the critical radius dissolve they will feed progressively more An-rich material into the residual magma, which in term will feed the growth of the larger crystals. When the rock is almost solid this effect could have an important influence on the last parts of the plagioclase crystals to form-the reversely zoned rims. The same general pattern of textural coarsening as recorded here by the plagioclase CSDs can be seen in the CSDs of other minerals in different rocks. A time-sequence of textural development was sampled in a drill-core that penetrated the upper part of the Makaopuhi lava lake (Cashman & Marsh, 1988). CSDs of samples with crystallinities from 20 to 80% have decreasing slopes and intercepts that pivot around a length of 0·1 mm (Fig. 14a). Cashman & Marsh, (1988) considered that these textures were produced by crystallization under conditions of linearly increasing undercooling. Hence, the nucleation density decreased with increasing crystallinity. However, if it is assumed that crystals only grew, and there was no resorption, then the CSDs of the more solid samples should record the first period of increasing nucleation density, following by decreasing nucleation density as the crystallinity increased from 20 to 80%. Such a CSD would have a peak that would migrate to greater lengths as crystallization proceeded, keeping a constant height and slope on either side. This is not what is observed, hence there must be resorption of smaller crystals during the period 20-80% crystallized, as was observed in the Nodular Troctolite of the LSJAC. The CN coarsening theory can reproduce the observed rotation of the CSDs around a fixed point. Figure
The Box Elder intrusion, Montana, is a 140 m thick laccolith of shonkinite (mafic syenite). The CSD of the clinopyroxene in the chilled margin is broadly linear with a slight curvature concave upwards, whereas the CSD from the interior is hump shaped with a shallower right-hand slope (Fig. 14b; Resmini, 1993). This feature closely resembles the coarsening observed in the Nodular Troctolite and was probably due to the same mechanism. The slight curvature of the chilled margin CSD suggests that coarsening had already started when the magma was chilled. Another example of coarsening is shown by chromite cumulates in the Stillwater complex (Waters & Boudreau, 1996). Centimetric layers rich in chromite were examined. Even in thin section the crystals in the centre of the layer are clearly larger and more abundant. The CSDs confirm that the centre has been coarsened, compared with the edges (Fig. 14c). This behaviour is consistent with the DeHoff model of coarsening, as the growth rate will be higher where the crystal edges are closer together. This type of positive feedback, reinforcing early, weak structures, has been explored by
Boudreau, (1987, and subsequent papers) and may account for the well-known `inch-scale' layering in the Stillwater complex. It is not surprising that metamorphic rocks also show evidence of coarsening. For instance, Cashman & Ferry, (1988) have studied garnets in regionally metamorphosed rocks of the Waterville formation, Maine, from chlorite zone to sillimanite zone. The shape and behaviour of the CSDs exactly follow those expected for increasing coarsening with increasing metamorphic grade (Fig. 14d). That lower-grade rocks do not coarsen as much as those at higher grade suggests that there is some kinetic barrier limiting growth. This may be mineralogical or topological. The following events are thought to have produced the textures observed in the Nodular Troctolite. The first phase to crystallize was olivine. It nucleated and grew in an environment of increasing undercooling. As the temperature dropped it was joined by plagioclase and the two continued to nucleate and grow together. At this time each phase had a linear CSD. The strong lamination of the early plagioclase indicates that the magma was flowing or being deformed at the time. Increasing undercooling was accommodated by removal of latent heat by the moving magma. Increasing crystallization impeded movement of the fluid component of the magma, hence latent heat could not be removed so readily. The temperature rose until it was just below that of the liquidus of plagioclase. There it was buffered by the solution and crystallization of plagioclase. At this temperature nucleation of both olivine and plagioclase was suppressed and textural coarsening started to occur. Small crystals were resorbed and larger crystals grew, both from recycled small crystals and new material in the magma. Both plagioclase and olivine were coarsened, but the largest olivine grains grew faster than the plagioclase as they were more undercooled. The olivine engulfed the plagioclase as it was coarsening and produced the poikilitic texture. Between the oikocrysts, plagioclase continued to coarsen until it had displaced all the magma. Maintenance of the temperature close to that of the first appearance of plagioclase for most of the duration of the crystallization prevented the nucleation and growth of other phases. A number of other points are important: I would like to thank Josée Désgagne for digitizing the sections, Tobi Cohen for directing me to references on Ostwald ripening, Michel Hervet for help in the field, and Sarah-Jane Barnes for comments on a draft of this manuscript. Reviews by Tony Fowler, Bill Meurer, Alan Boudreau and an anonymous reviewer helped improve the final manuscript. The Department of Geology, Université Blaise Pascal, Clermont-Ferrand, France, welcomed me during my sabbatical. This project was financed by a grant from the Natural Science and Engineering Research Council of Canada.INTRODUCTION
THE LAC-ST-JEAN ANORTHOSITE COMPLEX



NODULAR TROCTOLITE

CRYSTAL SIZE, SHAPE AND ORIENTATION DISTRIBUTIONS

Stereology-conversion of 2D data to three dimensions
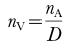
(1)
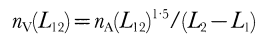
(2)
Results

DISCUSSION
Introduction
Initial plagioclase nucleation and growth

Textural adjustment-coarsening

(3)



(4)

(5)
Other examples of textural coarsening

CONCLUSIONS
ACKNOWLEDGEMENTS
REFERENCES