| Journal of Petrology | Pages |
© 1998 Oxford University Press |
Partial melting of peridotite in response to mantle upwelling is an important mechanism in the transfer of energy and mass between the mantle and the crust. This process occurs beneath mid-ocean ridges, oceanic islands, continental rifts and possibly above subduction zones, and is thus responsible for the formation of the most abundant igneous rocks on Earth and for much of the planet's continuing differentiation. Although forward modeling of partial melting during upwelling is in principle a relatively simple problem in classical chemical thermodynamics, it is in practice a challenging one because this process takes place over a range of pressures and acts on multicomponent, multiphase systems that evolve in composition as melts segregate from their sources. Because of the complexity of the thermodynamics of the phases involved, the limited available phase equilibrium data on peridotite melting, the continuous change in the composition of the system during ascent, and the complex relative motions of liquid and residual solid, considerable uncertainty remains about how peridotites melt when they ascend and melt. Experimental studies relevant to melting of mantle peridotite (e.g. Mysen & Kushiro, 1977; Stolper, 1980; Takahashi & Kushiro, 1983; Fujii & Scarfe, 1985; Falloon & Green, 1987, 1988; Kinzler & Grove, 1992a; Takahashi et al., 1993; Baker & Stolper, 1994; Walter & Presnall, 1994; Baker et al., 1995; Kushiro, 1996; Kinzler, 1997) are essential to understanding basalt petrogenesis. However, the results of such experiments, in which a peridotite of fixed composition is subjected to a specific temperature and pressure, cannot be related directly to a process occurring over a range of temperatures and pressures (and for which temperature is not an independent variable) and in which the bulk composition of the source peridotite changes continuously. A particular difficulty is that melting during upwelling probably approximates an adiabatic decompression (Verhoogen, 1965; McKenzie, 1984; Asimow et al., 1997), but partial melting experiments cannot be conducted under such conditions. To bridge the gap between experimental results and the processes that occur when mantle upwells and melts, many empirical parameterizations of peridotite melting have been devised (e.g. Klein & Langmuir, 1987;McKenzie & Bickle, 1988; Niu & Batiza, 1991; Kinzler & Grove, 1992b; Langmuir et al., 1992). Although these models differ in many ways, they are similar in that they all use results from experimental studies on peridotite melting to parameterize the extent of melting and the composition of partial melts as functions of temperature and pressure and then make independent assumptions to estimate the amount of melt produced during adiabatic upwelling of the mantle. Collectively, these parameterizations have been hugely successful in furthering our understanding of mantle melting processes. To take just one example, it is through application of such models that relationships between mantle temperature, crustal thickness, and average basalt composition have been predicted and then used to interpret the covariations of these parameters in the global mid-ocean ridge system (Klein & Langmuir, 1987; McKenzie & Bickle, 1988). The successes of these various parameterizations notwithstanding, such models have a number of shortcomings. All of them use convenient but not necessarily thermodynamically valid functional forms to fit the compositions of melts produced in experiments, and none of them explicitly relate chemical reactions to energetic balances. In these senses, these models are empirical rather than thermodynamic. As a result, these parameterizations are poorly suited to extrapolating outside the range of compositions, temperatures, and pressures of available experiments and therefore they cannot reliably predict aspects of peridotite melting behavior that have not already been elucidated experimentally. Also, because these models all assume simple relationships between energy balance and the extent of melting, little can be learned from them about the effects of bulk composition, melt extraction processes, extent of melting, etc. on melt production during upwelling. An alternative approach to modeling mantle melting is to employ thermodynamic models of minerals and melts and to calculate the phase equilibria of partially molten peridotite using the principles of energy potential optimization. This approach results in an internally consistent modeling of mantle melting that relates phase compositions to energetic inventories, that in all cases obeys mass balance constraints, and that behaves predictably in extrapolation. Thus, such calculations can potentially predict aspects of the phase equilibria of partially molten peridotites not already established from experiment. Furthermore, such models allow rigorous calculation of adiabatic and other conservative processes (e.g. isenthalpic), and therefore they can be used to aid understanding of the interplay between the chemical evolution of partially melting peridotite and melt production during mantle upwelling (Asimow et al., 1995, 1997). We note that what we call here the thermodynamic approach is also essentially empirical in that the thermodynamic properties of the phases involved are calibrated from experimental data. All thermodynamic models of real materials are, of course, empirical in this sense. However, not all empirical models are thermodynamic. Although many of the above-mentioned empirical models of mantle melting have aspects that are inspired by thermodynamic theory, none of them predict a specific relationship between the state of the system and the thermodynamic quantities (G, H, S, V, etc.) of its phases. Also, most of the models lack a complete mass-balance inventory of phases and components and therefore do not allow rigorous energy conservation. This means that such models cannot give information about energetic relationships between melt composition, residue mode, and melt-solid reaction. Direct thermodynamic calculation of peridotite melting does, however, have several disadvantages relative to the more empirical approaches. Because the phases of interest are compositionally and structurally complex, a great deal of information is required to construct thermodynamic models of these solid and liquid solutions, and some of the required information, such as the entropy of mixing of silicate liquids, is poorly known. In addition, the complexity of the phases and the complexity of energy minimization algorithms means that the thermodynamic calculation is computationally intensive, which makes it difficult to couple this approach with physical modeling. Additionally, the accuracy of this approach is not guaranteed, as the calibration is not constructed primarily from peridotite melting experiments. Finally, improvements in these models can be difficult to achieve because the source of errors or inaccuracies may be embedded in assumptions about any number of phases and therefore can be difficult to identify. The goals of this paper are to present the first thorough discussion of the application of a thermodynamic model to mantle melting. Calculations in this paper are confined to isobaric simulations, as an understanding of isobaric processes is a prerequisite to understanding polybaric processes. However, initial results of polybaric calculations have been presented by Hirschmann et al., (1994) and Asimow et al., (1995, 1997), and a more comprehensive treatment of polybaric mantle melting using this approach is in preparation. After brief introductions to the thermochemical models we use to describe mantle minerals and silicate liquid and to our energy optimization techniques, we illustrate the strengths and weaknesses of this approach by comparing predicted isobaric peridotite melting behavior with existing experiments. These comparisons are also evaluated for what they reveal about the shortcomings of our thermodynamic model and the improvements that will be required in future versions of this or other such models. In two companion papers (Hirschmann et al., 1998b,
1998c), we apply our model to evaluate several issues related to mantle melting processes including melt compositions near the dry peridotite solidus, variations in the amount of melt produced per increment of isobaric temperature increase (the isobaric productivity), and the effects of variability in peridotite composition on the composition of partial melts. The approach we take is to adopt thermochemical models for the solid and liquid phases relevant to mantle melting. For each phase, these models specify the relationship between the composition of the phase and the various thermodynamic potentials (e.g. G, H, S, V, etc.) as functions of pressure and temperature. Energy optimization techniques can then be combined with these models to calculate phase equilibria for any bulk rock composition that can be described as a mass balanced sum of the phases considered. Depending on the process being modeled, a different energy potential must be optimized to find the equilibrium assemblage. For example, the Gibbs free energy, G, is the thermodynamic potential that is minimized if temperature, pressure, and chemical composition are held fixed and is the most familiar energy potential used during optimization calculations (e.g. Van Zeggeren & Storey, 1970; Smith & Missen, 1982). As detailed below, some calculations in our work are performed by optimization of less familiar thermodynamic potentials. In all cases, however, the techniques used to calculate phase equilibria are implementations of energy optimization strategies that use iterative application of three separate algorithms. First, an estimate of the identity and composition of stable phases is made; second, the thermodynamic potential of interest is minimized subject to appropriate constraints on composition and other variables held constant (e.g. T and P in the case of G); and third, the resultant computed phases are checked for metastability relative to possible miscibility gaps or phases not included in the initial phase assemblage. To execute these steps, we use algorithms developed by Ghiorso, (1985, 1994). These algorithms, as well as the thermochemical models of minerals and melts detailed below, are encompassed in a single thermodynamic package known as MELTS (Ghiorso et al., 1994; Ghiorso & Sack, 1995). In this work, we use MELTS as well as some more specialized algorithms derived from the MELTS code. The solid phases of primary interest in the upper mantle are olivine, orthopyroxene (opx), cpx, plagioclase, spinel, and garnet. Because these are all complex solid solutions, they require estimation of both the standard-state properties of end-member mineral components (e.g. forsterite, fayalite, enstatite, etc.) and the mixing properties of the solid solutions. The properties of the end members of these minerals have been taken from the internally consistent database of Berman, (1988), except for those components that are not included in that database as detailed by Sack & Ghiorso, (1991a, 1991b, 1994a, 1994b, 1994c). The mixing models used for mineral solid solutions are summarized in Table 1. Table 1. Compositional range and sources of solid solution models
An important factor in the ability of thermodynamic models to replicate the phase equilibria of compositionally complex natural peridotites is the way in which minor components are handled. For example, oxides such as Na2O, Al2O3, TiO2, and Cr2O3 play key roles in the phase equilibria of natural peridotites both below and above the solidus. In partially molten peridotite, these oxides reside primarily in silicate liquid, in pyroxenes as typically minor non-quadrilateral components, and/or in spinel as major or minor components. Quantitative simulation of many important effects of mantle melting by the thermodynamic approach is particularly sensitive to the extent to which non-quadrilateral components are properly incorporated into the pyroxene solution model. Fortunately, Sack & Ghiorso, (1994a, 1994c) developed a model for pyroxenes that incorporates Na, Fe3+, Al, and Ti as well as the quadrilateral components. The most important component that is absent from the thermochemical models we have used is Cr2O3 in pyroxene. Cpx and opx from abyssal peridotites and spinel peridotite xenoliths typically contain 0·8-1·2 and 0·6-0·8% Cr2O3, respectively, which amounts to 30-70% of the Cr2O3 in these rocks (Nixon, 1987; Johnson et al., 1990; Johnson & Dick, 1992). The pyroxene models of Sack & Ghiorso, (1994a, 1994c) neglect Cr, but the spinel model (Sack & Ghiorso, 1991a, 1991b) includes it, so that in MELTS simulations all the Cr in the residual minerals goes into spinel. This probably results in slight underpredictions of cpx stability, but more importantly, it causes substantial overpredictions of the stability of spinel relative to plagioclase and garnet. For example, experiments on natural Cr-bearing lherzolitic minerals indicate that spinel disappears at pressures just slightly higher (O'Hara et al., 1971) than the initial appearance of garnet, but MELTS calculations predict that spinel persists at the peridotite solidus at all pressures. Silicate melts in the system SiO2-TiO2-Al2O3-Cr2O3-Fe2O3-FeO-MgO-CaO-Na2O-K2O-H2O are modeled using the solution model of Ghiorso & Sack, (1995). This model is a recalibration of the silicate liquid model first presented by Ghiorso & Carmichael, (1980) and Ghiorso et al., (1983) in which the liquid mixing behavior is approximated as a symmetric regular solution of mineral-like components (e.g. Mg2SiO4, CaSiO3, etc.). For a liquid of n components, the Gibbs free energy of the liquid, G, is described by
Here Smixing is the ideal entropy of mixing, N is the sum of ni, Xi are the mole fractions of the liquid components, R is the gas constant, and Wij are the symmetric liquid interaction parameters (Wij = Wji), which are constants independent of composition, temperature, and pressure. The standard-state chemical potentials of the liquid components are estimated from experimentally determined enthalpies of fusion of stoichiometric minerals or estimates of these quantities made by corresponding states approximations [references in Ghiorso & Sack, (1995)] and from experimentally calibrated parameterizations of the heat capacity, volume, thermal expansion, and compressibility of natural silicate liquids, which are generally known to better than 2% (Lange & Carmichael, 1987; Kress & Carmichael, 1991; Lange & Navrotsky, 1991). Because compressibilities are based on ultrasonic measurements at 1 bar and volume is fitted to a simple second-order expansion in terms of temperature and pressure, we believe that the liquid silicate properties are reliable only up to ~3 GPa. Although the enthalpies of fusion, [Delta]Hfus, of most important magmatic components are well known (Lange & Carmichael, 1990), [Delta]Hfus of forsterite, a key component relevant to partial melts of the mantle, has not been measured precisely. Ghiorso & Carmichael, (1980) derived an estimate of 170·1 kJ/mol for [Delta]Hfus of forsterite from analysis of the slope of the fusion curve, a value 50% higher than that estimated from extrapolation of calorimetrically determined enthalpies of fusion from intermediate compositions in the anorthite-forsterite binary (Navrotsky et al., 1989). More recent estimated values for [Delta]
Hfus of forsterite at its melting temperature and 1 bar have converged, as a direct calorimetric determination of [Delta]Hfus yielded 142 ± 14 kJ (Richet et al., 1993), and Ghiorso & Sack, (1995) recalculated the Navrotsky et al. determination using solid and liquid forsterite heat capacity functions from Berman, (1988) and Lange & Navrotsky, (1991) to yield the value of 124 ± 20 kJ applied in the present model. The liquid interaction parameters, Wij, are calibrated from experimentally determined mineral-melt phase equilibria by methods described by Ghiorso et al., (1983). The calibration database used for the present calculations, summarized by Ghiorso & Sack, (1995), contains 4666 statements of mineral-melt equilibria from 1593 experiments on natural compositions including liquids ranging in composition from komatiitic to rhyolitic to nephelinitic [see fig. 2 of Ghiorso & Sack, (1995)]. Most (~80%) of these experiments were performed at 1 bar; the calibration is therefore heavily weighted to match low-pressure phase equilibria. Of those experiments performed at higher pressure, many are from hydrous or silica-rich systems, and therefore are not necessarily directly applicable to peridotite phase relations. Studies related to peridotite melting that are included in the calibration database include those by Stolper, (1980), Takahashi & Kushiro, (1983), Takahashi, (1986) and Kinzler & Grove, (1992a). The paucity of direct constraints from peridotite partial melting studies reflects both the relatively small number of equilibrium mineral-melt pairs reported in many peridotite partial melting studies and the challenging experimental problems associated with these experiments. Many older studies were hampered by quench crystallization, non-ideal experimental geometries or containers, and/or run times inadequate to approach equilibrium. More recent studies related to peridotite partial melting (Hirose & Kushiro, 1993; Baker & Stolper, 1994; Bertka & Holloway, 1994; Baker et al., 1995; Longhi, 1995; Kushiro, 1996; Kinzler, 1997) have not been included in the current calibration. Future calibrations of the mineral and melt thermodynamic models (see below) will undoubtedly be improved by the availability of these studies. In principle, direct calibration from high-pressure phase equilibrium experiments is not needed for an accurate high-pressure liquid thermochemical model; i.e. knowledge of the 1 bar thermodynamic properties of the liquid phase and of the partial molar volumes of the liquid components and their pressure, temperature derivatives is sufficient to describe the liquid properties at high pressure. Likewise, if the adopted model is a valid description of the liquid mixing properties, it is not essential to have experiments on peridotite melting in the calibration database, as the interaction parameters describing the liquid properties can be determined from liquids significantly different in composition from those of interest to mantle melting. Thus, this approach has the potential to model accurately phase equilibria for liquid compositions and conditions of pressure and temperature outside the range previously subject to experiment. In fact, one of our motivations in not including the most recent high-pressure experiments in the calibration database was to explore the validity of some of the more surprising results of some of these experiments (Baker et al., 1995). If these experiments were included in the calibration database, it would not be particularly significant if the thermodynamic calculations reproduced their results. In practice, however, optimization of the calibration based on liquids close to the compositions of interest and at mantle pressures and temperatures would lead to improved accuracy. Consequently, as most of the constraints on the silicate liquid properties derive from 1 bar liquidus surfaces and prediction of phase equilibria at higher pressures represents an extrapolation in pressure and in composition (as cotectics are systematically displaced in composition with increasing pressure; e.g. Takahashi & Kushiro, 1983), there are inaccuracies in the high-pressure phase equilibria predicted by MELTS. Also, during calibration of pyroxene mixing properties, Sack & Ghiorso, (1994c) noted systematic discrepancies between fits to pyroxene-liquid equilibria from experiments at 1 bar and from those at higher pressure. Because the experimental database considered by Sack & Ghiorso, (1994c) and Ghiorso & Sack, (1995) was dominated by 1 bar constraints, Sack & Ghiorso, (1994c) and Ghiorso & Sack, (1995) chose values for their pyroxene and liquid calibrations that gave better fits to the 1 bar data at the expense of higher-pressure predictions. Thus, the current calibration is non-optimal for calculations at mantle pressures. Although there is clearly room for improvement of the chosen thermodynamic models for application to mantle melting at pressures up to a few GPa, we show below that this model does an excellent job of capturing most of the critical aspects of peridotite melting, and even some of its subtleties. It is important to note that the mineral-liquid experiments used in the calibration place constraints on the chemical potentials of the silicate liquid, but that the liquid interaction terms adjusted during the calibration, the W values, describe only deviations from non-ideal enthalpies of mixing. Other contributions to the liquid chemical potentials-the standard state properties and the entropy of mixing-are assumed before calibration. This approach, which is dictated in large part by the paucity of direct constraints on the entropies or enthalpies of mixing of natural silicate liquids and by the relative success in calibrating the chemical potentials using only temperature-independent liquid interaction terms (Ghiorso & Sack, 1995), has a number of consequences. First, it means that the silicate mixing model may constrain component chemical potentials better than it does the entropies or enthalpies of mixing; this is a common characteristic of thermodynamic models of liquids (Hildebrand & Scott, 1950). Second, it means that the liquid interaction parameters must compensate for any imperfections in the thermochemical models of the solid solutions and pure liquid components. They must also compensate for possible inadequacies of the liquid model, such as the assumption that liquid silicates mix as a regular solution or the approximation that the configurational entropy of liquid silicates is described by mixing of mineral-like components. These consequences notwithstanding, it appears, as described in the next two paragraphs, that the silicate liquid model in MELTS yields reasonable approximations to the entropies and enthalpies of magmatic liquids and does not introduce large errors to isenthalpic or isentropic calculations that depend on these mixing properties. The enthalpies of both modeled and real silicate liquids are dominated by contributions from standard state properties, not from mixing. For example, calculated enthalpies of mixing for basaltic liquids using MELTS are generally are typically near 60-90 J/g. These are similar in magnitude to those measured in simple systems (Navrotsky, 1987, [1995), and therefore probably reasonable for natural silicate liquids, though there are no direct measurements for the latter. Such values are ~10% of the measured enthalpies of fusion of key mantle minerals (e.g. diopside, 650 J/g; Lange et al., 1991; forsterite900 J/g; Ghiorso & Sack, 1995). Thus, the enthalpies of actual magmatic liquids are not likely to be significantly different from those calculated by MELTS. It is difficult to evaluate the applicability of the MELTS entropy of mixing model, as little is known about the entropy of mixing of natural or simple silicate liquids. Typical entropies of mixing for partial melts of peridotite calculated with MELTS are 0·12-0·14 J/K per g, about 30% of the entropy of fusion of important mantle minerals (e.g. diopside, 0·4-0·45 J/K per g; Lange et al., 1991; Ghiorso & Sack, 1995). The assumption embodied in MELTS that silicate liquids mix as molecules of mineral-like stoichiometry seems appropriate because: (1) the goodness of fit to crystal-liquid phase equilibria has no temperature dependence (Ghiorso & Sack, 1995), implying that the model used for the entropy of mixing is adequate; (2) the liquid chemical potentials are forced to agree with mineral-liquid equilibria and enthalpies of mixing are reasonable, so the entropy of mixing must not be grossly in error; (3) the magnitude of the derived entropies of mixing are comparable with other melt mixing models such as the two-lattice model for anorthite-albite-diopside liquids of Weill et al., (1980) or the speciation model for binary oxide-silicate liquids of Hess, (1995) (although such comparisons are not without problems, as apportionment of entropy between mixing and standard state terms depends on the complexity of compounds employed in the model). Even if the assumed entropy of mixing model is flawed, entropies of silicate liquids modeled with MELTS are likely to be more accurate than those modeled with previous treatments of melting energetics (Hess, 1992; Iwamori et al., 1995) given that earlier models have not accounted for the entropy of mixing of silicate liquids at all. We also note that, unlike previous treatments, MELTS accounts for the entropy of mixing of solid solutions. The fO2 evolution of natural magmas and of partially melting peridotite is controlled primarily by the interplay between the Fe2+/Fe3+ redox couple and the oxidized and reduced species in the system C-H-O-S (Carmichael & Ghiorso, 1986). Because the thermodynamic models applied do not incorporate C- and S-bearing species, calculated closed system paths may not accurately simulate realistic fO2 paths. For calculations in this study, f
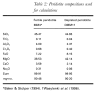
O2 is constrained to remain fixed relative to a reference solid buffer assemblage such as quartz-fayalite-magnetite (QFM) by minimization of the Korzhinskii potential, which is minimal at fixed T, P, and µO2 (Ghiorso & Kelemen, 1987), instead of the more familiar Gibbs free energy potential. Minimization of the Korzhinskii potential requires adding or removing small amounts of oxygen to the system to match the liquid Fe3+/Fe2+ ratio appropriate for the buffer, guided by the calibration of Kress & Carmichael, (1991). Calculations in which the total oxygen content of the system is held constant and the oxygen fugacity of the system is allowed to evolve in response to redistribution of Fe3+ and Fe2+ during melting and/or melt removal have also been done, but are not reported here. MELTS incorporates a simple parameterization of the effect of water on magmatic phase equilibria (Ghiorso & Sack, 1995) based on the assumption that the activity of water is proportional to the square of its concentration. This parameterization is developed primarily from measured solubilities of water in silicate melts, rather than from experimental constraints on the effect of water on liquid-mineral phase equilibria. Thus, it is unlikely to capture the detailed effects of water on melting relations. Also, the parameterization does not account for speciation of water between hydroxyl ions and water molecules (Silver & Stolper, 1985), and the functional form of the water equation of state adopted in the present version of MELTS fails above 1 GPa. However crude, the MELTS formulation, unlike other parameterizations of peridotite partial melting, incorporates the energetic effects of water such that melt production of slightly hydrous peridotite can be treated in a quantitative, internally consistent fashion. It is generally accepted that basaltic melts form interconnected networks in peridotite even at small melt fractions (Waff & Bulau, 1979; Cooper & Kohlstedt, 1982; Von Bargen & Waff, 1986; Daines & Richter, 1988) and that rapid separation of melt from the source results in a melting process that more nearly approximates fractional fusion than it does batch melting (McKenzie, 1984, 1985, Richter & McKenzie, 1984; Salters & Hart, 1989; Johnson et al., 1990; Riley & Kohlstedt, 1991). Thermodynamic calculations can simulate isobaric fractional fusion by incremental isobaric batch fusion; i.e. by the repeated increase in temperature sufficient to generate small fixed increments of melt by batch fusion, followed by removal of the melt generated. For the fractional melting calculations presented below, increments of 1% melting were used. Calculations have been done using smaller melting increments (0·5%, 0·1%), but the results do not differ significantly from those based on the 1% melting increments. To explore the strengths and weaknesses of the thermodynamic calculations, we compared the predicted and the experimentally measured proportions and compositions of melts produced at 1 GPa for a fertile (MM3) and a depleted (DMM1) peridotite composition (Table 2) for which there are detailed experimental results (Baker & Stolper, 1994; Baker et al., 1995; Wasylenki et al., 1996). Calculated melt and mineral compositions and proportions are given in the Appendix. We also compare the calculated effect of removal of liquid during melting with the incremental batch fusion experiments of Hirose & Kawamura, (1994) and the calculated effect of addition of water on the proportion of melt generated with the experiments of Hirose & Kawamoto, (1995). We emphasize that none of the experiments used for these comparisons were used to calibrate MELTS, so the calculations are independent predictions of peridotite melting trends. Table 2. Peridotite compositions used for calculations
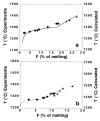
For the fertile peridotite (composition MM3, Table 2), energy potential minimization correctly predicts that the stable minerals in equilibrium with silicate liquid near the solidus are olivine, aluminous opx, aluminous cpx, and at least one additional aluminous phase. Plagioclase (An48) is predicted below 0·6 GPa and garnet above 3·05 GPa. Spinel is predicted to be stable at all pressures (owing to the absence of Cr in other mineral models). Between 0·6 and 3·05 GPa, it is predicted to be a Cr-Al-rich spinel; above and below these pressures, the calculated spinel is nearly pure chromite that is volumetrically subordinate to plagioclase or garnet. Other minerals considered during the calculation but not predicted to be stable are quartz, cristobalite, tridymite, ilmenite, rutile, orthorhombic Fe-Ti oxides, nepheline, melilite, titanite, perovskite, aenigmatite, and corundum. The low pressure at which plagioclase lherzolite appears in these calculations reflects the high Cr2O3 content of MM3 (0·68%; Table 2). For peridotite compositions with more typical Cr2O3 contents, such as the LOSIMAG model mantle composition (0·47% Cr2O3; Hart & Zindler, 1986), initial stability of plagioclase on the solidus is predicted to be near 0·9 GPa. The calculated sequence of phase disappearance during progressive partial melting of the MM3 fertile peridotite composition at 1 GPa spinel peridotite is cpx (at 18% melting), opx (at 65% melting), spinel (at 93% melting), and then finally olivine. This sequence agrees with experimentally well-established phase relations in the melting interval of spinel peridotite (e.g. Takahashi & Kushiro, 1983), although the extent of melting required to eliminate spinel from the solid residue varies depending on the Cr2O3 content of the peridotite. This agreement demonstrates that the predicted `phase diagram' of spinel peridotite is semi-quantitatively correct, which is a prerequisite for applying this technique to understanding of mantle melting. Calculated proportions of residual minerals coexisting with partial melts of MM3 peridotite at 1 GPa are compared with those determined from experiments by Baker & Stolper, (1994) in Fig. 1. The phase proportions in the experiments are estimated from a least-squares fit of the proportions of the analyzed phases in the experiment to the bulk composition. Residual mineral proportions are shown as a percent of total (solid + liquid) mass. Both calculations and experiments show that cpx is the chief phase entering the melt during the early stages of melting. In the calculations, cpx is exhausted from the residual assemblage at a slightly lower extent of melting (18%) than indicated by the experiments (22%). For a more depleted composition, DMM1 (Table 2), the predicted exhaustion of cpx at 1 GPa occurs after ~7% melting, slightly lower than the ~8-10% indicated by experiments on this composition (Wasylenki et al., 1996). For MM3, both the calculated and experimentally determined proportions of olivine change little during the early stages of melting, but calculated olivine mass fraction is systematically lower than that inferred from experiments. The slight increase in calculated and experimentally determined olivine mass fraction during the first ~15% melting is indicative of olivine being in reaction relationship, although the effect is better developed in the experiments. Above ~15% melting, calculated proportion of olivine decreases slightly whereas that experimentally determined olivine mass is nearly constant. Calculated and experimentally determined masses of opx are similar at low melt fraction, and both show significant decreases following the exhaustion of cpx. However, above ~15% melting, the calculated mass of opx is systematically higher than that indicated by the experiments. The calculations predict that opx is in reaction relation between ~8% melting and cpx exhaustion, a feature not seen in the experiments. The calculated spinel mass is higher than that derived from the experiments throughout the melting interval; this reflects the exclusion of Cr2O3 from the pyroxene thermochemical models. Overall, this comparison indicates a good correspondence between calculations and experiments, except that in the calculations, opx is too stable and olivine is not stable enough. Figure
For the MM3 and DMM1 compositions, the model melt mass fraction (F) as a function of temperature is displayed in Fig. 2. In the calculations, the temperature required to generate a given fraction of liquid is systematically ~100°C higher than it is in the MM3 experiments and ~120°C higher than it is in the DMM1 experiments. These differences are related to the differences between melt compositions calculated by MELTS and those determined experimentally (see below). Although this temperature offset prevents application of MELTS in its present form to such problems as the potential temperature of the mantle, the shapes of the calculated and measured melt fraction vs temperature functions for these two compositions are in good agreement. This suggests that MELTS may provide valuable insights into the isobaric melt productivity [i.e. ([part]F/[part]T)P], which although generally poorly known is of great importance in modeling mantle melting (Asimow et al., 1995, 1997). Figure
For calculations on the fertile MM3 composition, exhaustion of cpx is accompanied in the calculations by a decrease in ([part]F/[part]T)P from 0·45%/°C before cpx-out to ([part]F/[part]T)P = 0·1%/°C afterwards (Fig. 2). For the depleted DMM1 composition, the calculated change in slope is similar. Such a dramatic calculated change in productivity is not clear in the experiments on the MM3 composition by Baker & Stolper, (1994). On the other hand, experimental results on DMM1 do suggest a drop in productivity at this point, although the scatter in the experimental T-F determinations is considerable. A decrease in ([part]F/[part]T)P on exhaustion of cpx has also been documented in diamond aggregate experiments on a fertile peridotite of different composition from MM3 (PHN-1611; Kushiro, 1996). It is not clear whether experimentally determined differences in T vs F behavior at cpx exhaustion between MM3 and PHN-1611 reflect experimental artifacts or bulk composition effects, but MELTS calculations and a more general treatment of the effects of phase exhaustion on melt productivity in simple and complex systems (Asimow et al., 1997) suggest that sharp decreases in productivity are the expected behavior following phase exhaustion. Thermodynamic calculations of melt fraction vs temperature for the MM3 composition suggest that ([part]F/[part]T)P is very small at the solidus, but increases dramatically between 0 and ~4% melting (Fig. 2). For example, calculated ([part]F/[part]T)P increases from ~0·025%/°C at 2% melting to 0·09%/°C at 4% melting, and then increases more slowly but steadily to values of >0·4%/°C just before cpx-out at 18% melting. In contrast, the calculated increase in productivity for DMM1 is of smaller magnitude and is pronounced only below 1% melting. Although the marked increase in productivity at low melt fractions has not been observed experimentally for MM3 (Baker & Stolper, 1994; Baker et al., 1995), it has been detected in other experiments on natural peridotite (Mysen & Kushiro, 1977) and for analogues of peridotite compositions in the system NCMAS (Walter & Presnall, 1994). The region of low calculated productivity near the solidus of MM3 (Fig. 2) corresponds to the region where the composition of the calculated liquid is changing rapidly (Fig. 3). The link between these two phenomena is predicted from a general analysis of melt productivity in systems with solid solutions (Asimow et al., 1997) and is discussed in greater detail in the companion paper (Hirschmann et al., 1998c). However, as detailed in that paper, there is reason to believe that the MELTS-calculated near-solidus downturn in productivity is exaggerated relative to actual peridotite melting behavior. Figure
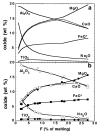
Calculated liquid compositions at 1 GPa for partial melting of the fertile peridotite MM3 are shown in Figs 3 and 4 and define the following overall trends. Concentrations of MgO, FeO* and Cr2O3 (not shown in Fig. 3) increase with increasing melt fraction. That of CaO increases until cpx is exhausted from the residue, but then decreases with further melting. The Al2O3 content decreases with increasing melt fraction, as do the Na2O and TiO2 contents, except between the solidus and ~5% melting, where the TiO2 content increases with increasing melt fraction. The decrease in the concentration of Na2O is particularly sharp during this first 5% of melting. SiO2 concentration varies little as a function of melt fraction, except between the solidus and 5% melting where the SiO2 content decreases sharply with increasing temperature (Fig. 4). As shown in Figs 3 and 4, all of these trends agree remarkably well with the 1 GPa piston cylinder experiments of Baker & Stolper, (1994) and Baker et al., (1995) on this composition. Most notably and as emphasized by Baker et al., (1995), as temperature is initially increased from the solidus to a few percent melting, both calculations and experiments show the same sharp decrease in silica content and the moderate increase in TiO2 content, features that are contrary to expectations based on previous experimental studies (e.g. Mysen & Kushiro, 1977; Stolper, 1980; Takahashi & Kushiro, 1983; Fujii & Scarfe, 1985; Falloon & Green, 1987, 1988; Kinzler & Grove, 1992a; Hirose & Kushiro, 1993) or based on previous empirical parameterizations of mantle melting (McKenzie & Bickle, 1988; Niu & Batiza, 1991; Kinzler & Grove, 1992b; Langmuir et al., 1992; Walter & Presnall, 1994). Also, both calculations and experiments suggest that relative to higher-degree melts, near-solidus melts have CaO, MgO, and FeO* contents that are significantly reduced relative to expectations based on earlier experiments or models. Figure
Quantitatively, calculated and experimentally determined concentrations are in excellent agreement for some oxides, less so for others (Figs 3 and 4). Calculated and experimental trends for FeO*, Cr2O3, and TiO2 contents are nearly identical. Trends in the concentration of Al2O3 are essentially parallel, with calculated abundances 1-2 wt % lower than experimental values. Calculated trends for CaO and MgO are systematically higher than experimental values; between 2 and 3 wt % in the case of CaO and between 2 and 4 wt % in the case of MgO, although the disagreement narrows at low melt fraction. Na2O contents agree well at high melt fraction, but near the solidus the calculated values climb to values significantly higher than in the experiments. Calculated concentrations of SiO2 are systematically lower than experimental values by 3-4% (Fig. 4). It should be noted that the respective high and low calculated values of MgO and SiO2 reflect the calculated understability of olivine and overstability of opx noted above (see Fig. 1). Melting relations for the depleted peridotite composition DMM1 have recently been determined experimentally (Wasylenki et al., 1996); experimental and calculated 1 GPa trends in liquid composition are compared in Fig. 5. Experimentally determined trends (Wasylenki et al., 1996) in oxide concentration are qualitatively similar to those for fertile peridotite, except that the CaO content peaks at a lower melt fraction (~10%), reflecting the lower modal abundance of cpx in this composition, and the trend in TiO2 concentration does not reverse slope at low melt fractions (Fig. 5). Another difference in the experimentally determined trends is that changes in SiO2 content near the solidus of the depleted composition are much less pronounced than those observed for the fertile MM3 composition. As with the fertile peridotite composition, the calculated and experimentally determined trends in melt compositions for the depleted DMM1 composition are qualitatively similar, but in detail calculated concentrations of some oxides are displaced from the measured values (and again in essentially the same way as in the MM3 composition). In particular, calculated SiO2 and Al2O3 contents are several percent lower than the experimental determinations, whereas the calculated MgO and CaO contents are systematically higher than the experimental determinations (Figs 4 and 5). Figure
A key feature of the comparison between the calculated and experimentally determined melt compositions for the depleted DMM1 composition is the behavior at low melt fraction. For the fertile MM3 composition, both theoretical and experimental results suggest large increases in SiO2 with decreasing melt fraction in the region below 5% melting. In contrast, for the depleted DMM1 composition, the calculations suggest that SiO2 content remains constant except at very low melt fraction (<2% melting), where there is a modest increase. Experiments on DMM1 do not document melt fractions below 3% melting, but also suggest that changes in SiO2 in the low melt fraction region (<5%) are small (Fig. 4). In addition, the turnover in the trend in TiO2 content observed in the experimental and calculated results for fertile peridotite is not observed in the experiments on the depleted peridotite composition and is predicted to occur only at very low melt fractions (<1%). In our view, these agreements between experiments and calculations provide strong support for the view that the unexpected behavior reported by Baker et al., (1995) at low melt fraction for MM3 is not an experimental or computational artifact; i.e. this behavior is only observed experimentally for the composition for which it is predicted by the thermodynamic calculations, and it is not observed experimentally in the depleted composition for which it is not predicted by the calculations. We think it would be remarkable for an experimental artifact to so faithfully reproduce the trends independently calculated based on MELTS. As discussed further by Hirschmann et al., (1998c), we infer that the differences between the trends at low degrees of melting of the MM3 composition and the DMM1 composition largely reflect the differences in alkali contents of their near-solidus melts. Figure 6 shows the calculated melt fraction vs temperature trends for batch and fractional fusion of the MM3 composition at 1 GPa. As shown by Asimow et al., (1997), the isobaric productivity, ([part]F/[part]T)P, for fractional fusion and batch fusion must be identical right at the solidus. However, after the first increment of melting and then up to several percent melting, the isobaric productivity for fractional fusion is significantly smaller than that for batch fusion; i.e. achieving 3% melting by incremental batch fusion requires a temperature increase 20°C greater than achieving the same extent of melting by batch fusion. However, a key prediction of the MELTS calculation, and one that to our knowledge has not been anticipated in previous calculations, is that following the first several percent of melting, the isobaric melt productivities for fractional and batch fusion become similar (~0·45%/°C) and remain so from ~3% melting up until the disappearance of cpx. Figure 6 shows that the calculated T vs F paths are roughly parallel for fractional and batch melting, with the fractional melting trend displaced to about ~20°C higher temperature. Following exhaustion of cpx, the predicted productivity of near-fractional melting is markedly smaller (0·05%/°C) than that of batch melting (0·1%/°C). Figure
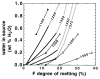
The calculated isobaric productivity during fractional melting can be compared with the sequential batch partial melting experiments of Hirose & Kawamura, (1994), which were designed to simulate the effects of melt production in a fractionally melting mantle. A series of batch melting experiments were conducted where the bulk composition approximated the solid residue of the preceding experiment. The initial experiment was performed with peridotite composition PHN-1611 and subsequent experiments were done with synthetic gels. The experiments differ from actual fractional processes and from our simulations in two significant ways. First, the increments of melting between each experiment ranged from 3 to 10%, with the first increment being 10%. Second, the compositions synthesized were not identical to actual residues of previous melting steps, as they were spiked with K2O, such that melts formed always had 1-3% K2O. Despite these differences, the study of Hirose & Kawamura, (1994) provides the only available experimental guide for the behavior of isobaric fractional melting of peridotite and thus is an independent test of the results of the MELTS calculation. We regard it as a success of the MELTS model that, just as for our calculations, their results suggest that melt production is inhibited during the early stages of fractional melting, but that following the early stages of melt extraction (>10% melting), productivity for fractional melting is similar to experimentally determined batch productivity for the same bulk composition (Fig. 6 inset). The absolute temperature offsets between incremental batch and batch melting are greater for the experiments than for the calculations, but the qualitative results compare favorably in that rates of isobaric fractional and batch melting are most different during the first increments of melting and become similar during later increments. Although not generally recognized, the increase in productivity with increased melting inferred by Hirose & Kawamura (for incremental batch fusion) and predicted by MELTS (for incremental batch and for batch fusion see Figs 2 and 6) is likely to be an important general feature of magma generation. This feature can be readily understood from consideration of the general expression for isobaric productivity (Asimow et al., 1997). A more detailed discussion of the reasons for productivity variations in batch and fractional melting is given by Hirschmann et al., (1998c). The effect of H2O on peridotite partial melting has been predicted with MELTS by calculating phase equilibria at fixed temperature and pressure as a function of total water content. As in the previous sections, the results of such calculations can be compared with peridotite partial melting experiments performed with variable total water contents (e.g. Hirose & Kawamoto, 1995). Again, as the results of such experiments are not part of the calibration database of MELTS, such a comparison serves as an additional independent test of the degree to which the MELTS calculations capture the actual nature of peridotite melting. The experiments of Hirose & Kawamoto, (1995) are the only published partial melting experiments of peridotite containing small amounts of water, but caution is necessary in interpreting these data. This is because: (1) the amounts of water in these experiments were estimated only from the amount of water loaded into each experiment, but direct analysis of selected glasses showed that there was considerable water loss over the course of at least some of the experiments; (2) the melt fraction in these experiments was estimated from microprobe analyses of glasses based on the assumption that Na behaved as a perfectly incompatible element, rather than from mass balance calculations. Starting with the dry, fertile peridotite MM3 at 1 GPa and at QFM, the effect of addition of H2O on melt fraction was calculated for the case of batch melting by adding small increments of water to the bulk composition and determining the stable assemblage (Fig. 7). Calculations at QFM + 2 yield similar results. For a given temperature and water content, MELTS calculations predict considerably less melting than the experiments of Hirose & Kawamoto, (1995). This difference is inherited from the anhydrous part of the calculation, as the same effect was noted in comparing the dry calculations with experiments (see Fig. 2). As in the comparison of the anhydrous experiments and calculations, the key to evaluating the MELTS calculations is a comparison of the trends with increasing temperature and water content, and from this perspective, the experiments and calculations have similar features (Fig. 7). Both show that at a given temperature, the total water vs melt fraction curves are concave up (i.e. the increase in melt fraction with addition of water to the system is larger at lower total water contents), but the MELTS calculations show that the apparent curvature is primarily a result of a break in slope upon the exhaustion of cpx. For extents of melting less than those needed to exhaust cpx from the residue, the calculations and experiments also both show significant increases with increasing temperature in the amount of melt generated per increment of water added. Under these conditions, the slopes of the calculated and measured melt fraction vs water content curves are similar, but the calculations suggest a greater change in
Figure
An important prediction of the calculations is that before cpx exhaustion, melt fraction is roughly linear with the amount of water added. The experimental data are not sufficient at this point to test the prediction of a roughly linear relationship in the lherzolite field, as there are no more than two experiments with that assemblage at any temperature. Although Hirose & Kawamoto, (1995) emphasized the non-linearity of the trend in added H2O and melt fraction our calculations suggest that this non-linearity is probably largely a consequence of a change in slope at cpx exhaustion. Further work will be needed to clarify the relationship between melt fraction and water content beyond cpx exhaustion. The preceding discussion demonstrates that there is a significant correspondence between the results of thermodynamic calculations using MELTS and experimental studies of the partial melting of peridotite (e.g. Figs 1-7). However, there are systematic differences between the calculations and experiments that highlight some of the limitations to current thermodynamic models and to their utility for accurate modeling of peridotite melting. The most prominent shortcomings of the current calibration of MELTS with respect to mantle melting are the systematic offsets of the calculated SiO2-F, MgO-F, and T-F relations relative to the results of peridotite melting experiments. These inaccuracies, as well as the low calculated modal olivine/orthopyroxene ratios indicated by Fig. 1, are all symptoms of the same problem, namely that for the coexistence of magnesian opx, olivine, and liquid in the pressure and temperature range of interest, MELTS fixes the chemical potential of SiO2 at too low a value. This results in calculated intersection of olivine and opx liquidus surfaces at too high a normative olivine content, too high a temperature, and therefore at liquid compositions that are too high in MgO and poor in SiO2. This inaccuracy also affects other aspects of the calculations. For example, because calculated melting temperatures are too high, coexisting pyroxenes are fixed at a more narrow part of the pyroxene solvus, causing cpx compositions to contain too little CaO. This affects the stoichiometry of the melting reaction, increasing the proportion of cpx entering the melt, and possibly influencing the extent of melting required to exhaust cpx (Fig. 1) and the CaO contents of calculated melts (Figs 3 and 5). It is possible that these problems originate primarily from errors or uncertainties in the calculated relative stabilities of olivine and opx (i.e. that relative to opx, the Gibbs free energy surface of the olivine solid solution in MELTS is slightly higher than it should be), rather than from uncertainties in the liquid properties. For example, the Sack & Ghiorso olivine model, which includes relatively large positive deviations from ideality, may not sufficiently stabilize olivine at the temperatures most relevant to mantle melting processes (>1250°C). The substantial non-ideality in this olivine model was inferred primarily from analyses of olivine-opx equilibria at <750°C (Sack & Ghiorso, 1989). Subsequent analysis of equilibria involving olivine, opx, cummingtonite, magnetite, and quartz has confirmed the validity of the model between 500 and 750°C (Ghiorso et al., 1995) and reports of spinodal decomposition in meteoritic olivine (Petaev & Brearley, 1994; Petaev, 1996) are consistent with marked non-ideality at low and intermediate temperatures. On the other hand, experiments at higher temperatures (800-1150°C) imply smaller deviations from ideality than the Sack & Ghiorso model (Wiser & Wood, 1991; Koch-Muller et al., 1992; Von Seckendorff & O'Neill, 1993). The apparent incompatibility of the olivine and opx models at high temperature and the problems with the MELTS calculations on peridotite at high temperature might all be resolved if the free energy of mixing of olivine were taken to be temperature dependent, leading to more ideal behavior of olivine at high temperatures. Rather than reflecting a problem with the thermochemical model for olivine (resulting in it being a little less stable relative to opx than it should be at high temperature, as explained in the previous paragraph), it is also possible that these discrepancies in MELTS might be resolved by adjustments to the free energy surface of enstatite-rich pyroxenes that would decrease the stability of orthopyroxene relative to olivine. In particular, the observed discrepancy would be the result if the Berman, (1988) standard state for end-member enstatite that was adopted by Sack & Ghiorso, (1989) is more stable at high temperature than is warranted. This is plausible given that measurements of the properties of MgSiO3-rich pyroxenes are complicated by the existence of several high-temperature polymorphs. The crystal chemistry of Mg-rich (Mg,Fe)SiO3 pyroxene above 1000°C is further complicated both by anomalous ordering behavior and by unusual structural rearrangements associated with the continuous transition from the opx to the proto-pyroxene structure (Yang & Ghose, 1994, 1995). As pointed out by Berman & Aranovich, (1996), these crystal-chemical complications may explain why existing thermodynamic models for opx have difficulty reconciling phase equilibrium constraints with observations of cation ordering. As a demonstration of how inaccuracies in thermodynamic variables may affect the calculated silica contents of partial melts of peridotite, we have arbitrarily varied the stability of opx while holding all other parameters in MELTS constant and then recalculated partial melting trends of MM3 peridotite. The results of such calculations are shown in Fig. 8 and suggest that a 2-3 kJ/mol increase in the free energy of opx (achieved by arbitrarily increasing the enthalpy of formation of enstatite and ferrosilite) is sufficient to account for the difference between observed and calculated SiO2 contents of partial melts of peridotite. It should be noted that this simple adjustment would not be an appropriate `fix' to the MELTS model, because adjusting the stability of opx without recalibration of other properties would cause many other aspects of the calculation (such as Fe-Mg exchange equilibria, relative stability of opx vs cpx, etc.) to shift. Incorporation of changes of opx stability into a revised more accurate MELTS model would require recalibration of both mineral and melt models. Nevertheless, Fig. 8 does give a feeling for the relationship between energetic parameters in MELTS and composition of predicted phases, and points the way towards one potential strategy for improving MELTS. It should also be noted that adjustments to the stability of other phases (e.g. olivine or liquid) required to resolve the compositional discrepancies would not necessarily be of the same magnitude (though they may be similar), as the stable liquid composition depends on the locus of points of common tangency to the G-X surfaces of each phase. Changes in the G surface of a particular phase shift the common tangents to different extents, depending on the composition and the G-X relationship for that phase. Figure
An alternative to laying the blame for these inaccuracies in the MgO and SiO2 contents of olivine + opx-saturated liquids at high pressure on the thermochemical models of olivine and/or opx is that the problem is with the liquid model; i.e. MELTS could fix the Gibbs free energy of silicate liquid at too low a value, relative to ol and opx. This would result in the liquid coming into tangency with ol and opx at a composition too poor in SiO2 and at too high a temperature, as is observed. If the error does lie with the liquid, we think it is unlikely that the cause is a problem with the liquid mixing model, because there is a consistent offset between predicted and experimentally determined silica and magnesia contents over a substantial range of liquid compositions (Figs 3 and 4) (although, as pointed out above, the liquid mixing model absorbs errors from other parts of the model, and therefore errors originating in mineral models or liquid standard state properties could manifest themselves as errors in the liquid mixing properties). However, it is possible that predicted high-pressure phase equilibria are affected by inaccuracies in the adopted equation of state (EOS) for silicate liquid. For example, either the total calculated volume of high-pressure liquids could be too small (resulting in a calculated liquid G that is too low) or the high-pressure partial molar volume of SiO2 could be too large relative to that of MgO (resulting in a G surface that comes into tangency with ol + opx at compositions that are too SiO2 poor.) Recently, Gaetani et al. (1998) have presented experiments that suggest pressure variations in the partial molar volume of SiO2 in rhyolitic liquids that differ from those calculated with the EOS used by MELTS. However, the EOS employed by MELTS and suggested by Gaetani et al. yields values for the integral
INTRODUCTION
DESCRIPTION OF THE CALCULATION TECHNIQUE
Review of thermodynamic models for minerals and melts

where �0i and ni are the chemical potentials and number of moles of liquid component i, Gideal is
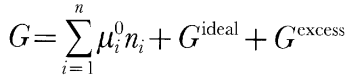
(1)
and, for a symmetric regular solution,
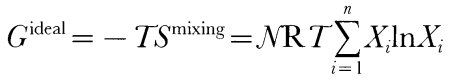
(2)
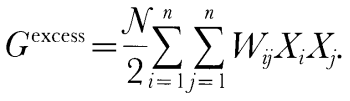
(3)
Redox evolution during partial melting
Calculations involving hydrous silicate liquid
Incremental batch melting calculations
COMPARISON OF MELTS CALCULATIONS AND PERIDOTITE PARTIAL MELTING EXPERIMENTS
Predicted residual phases and mineral modes

Isobaric melt production
Calculated melt compositions


Incremental batch melting

Melting of peridotite in the presence of water
(where XwH2O is wt % H2O) with increasing temperature than indicated by the experiments (Fig. 7). For harzburgitic (cpx-free) residues, the calculations suggest that the effect of water on melt production is reduced dramatically. There is a suggestion of similar behavior in the experiments at 1200 and 1300°C, but not in the experiments conducted at 1350°C.
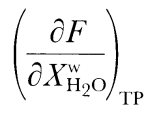
PROBLEMS WITH APPLYING THE PRESENT MELTS CALIBRATION TO MANTLE MELTING

that differ by only 70 J/mol. As this integral reflects the contribution of the EOS to the chemical potential of SiO2 at 1 GPa, it is unlikely that inaccuracies in the MELTS EOS can account wholly for the observed differences in calculated and experimentally measured liquid compositions at 1 GPa unless larger inaccuracies are present in the MELTS-calculated partial molar volumes for other melt components (e.g. MgO).

A second inaccuracy of the MELTS calculations is that the calculated Na2O contents of liquids near the solidus are consistently too high (Fig. 3). According to the MELTS calculations, the partition coefficient for Na between cpx and liquid at 1 GPa increases from 0·05 at the solidus to 0·10 at the exhaustion of cpx. These values are lower than those typically measured for coexisting phases in experiments relevant to peridotite partial melting near 1 GPa (0·10-0·20; Kinzler & Grove, 1992a; Baker & Stolper, 1994; Blundy et al., 1995). The low calculated values of Dcpx/liqNa lead to anomalously high Na2O contents of liquids near the solidus and these in turn cause exaggerations in near-solidus variations in calculated isobaric productivities (Fig. 2), and probably in the predicted enhancement in SiO2 in low-degree melts. Also, too-low solubility of Na in cpx probably leads to a calculated stability of plagioclase that is greater (and a plagioclase that is more sodic) than observed in nature or experiments. It is important to emphasize that although this discrepancy can be described in terms of a simple pyroxene-liquid partition coefficient, this partition coefficient is a derived parameter in the MELTS models, reflecting the solution models adopted for the Na-bearing phases, and is therefore not as easy to adjust as in non-thermodynamic models that simply specify such partitioning behavior (McKenzie & Bickle, 1988; Niu & Batiza, 1991; Kinzler & Grove, 1992b; Langmuir et al., 1992). In this context, the agreement between experiment and prediction is actually fairly good. The discrepancy can be traced to the calibration of the cpx solution model of Sack & Ghiorso, (1994c), which for experiments with coexisting cpx and liquid systematically underpredicts the Na contents of the cpx. For example, for a suite of representative 1 bar experimental augite-liquid pairs (Sack & Ghiorso, 1994c), MELTS predictions of the Na contents of cpx are typically 70% of the experimentally measured concentrations (Fig. 9). This underprediction originates from a compromise made by Sack & Ghiorso, (1994c), who were attempting to fit simultaneously the properties of a large number of cpx substituents (Na+, Ti4+, Al3+, Fe3+) using a database dominated by 1 bar cpx-liquid pairs in which Na-rich pyroxenes primarily coexisted with highly alkalic liquids. To prevent prediction of a stable Na-rich, Ti-rich cpx coexisting with augite in these liquids, Sack & Ghiorso chose to underpredict the stability of sodic substitutions in cpx.

Figure
As noted above, an additional cause of disagreement between calculated and experimentally determined compositions of partial melts of peridotite is the absence of Cr2O3 in the pyroxene mixing model. This increases the mode of calculated spinel relative to that seen in experiments. In addition, although too much Cr is calculated to be present in spinel because none of it is taken up by pyroxene, the Cr/Al ratio of the spinel cannot be larger then that fixed by CrAl-1 exchange equilibrium with the silicate liquid. Thus, extra Al must substitute into the spinel, thereby increasing the spinel mode and reducing the total amount of Al available for substitution in other phases, including the liquid. We think that this is largely responsible for the low Al2O3 in calculated liquids relative to those documented in experiments. The extra MgO also taken up by spinel may likewise contribute to the low predicted ol/opx ratio (Fig. 1). This discussion illustrates the complex interdependence of compositional variables in phase equilibrium problems when approached from a thermodynamic perspective; i.e. it is remarkable and could not have been fully anticipated that the failure to take proper account of ~1% of Cr2O3 in pyroxenes can introduce significant errors into the concentrations of major components such as alumina and magnesia in the equilibrium liquids. This in turn emphasizes two of our previous points: (1) Even though seemingly simple adjustments to the thermodynamic models might at first appear to be the proper approach to correcting some of the inaccuracies in the results of MELTS calculations, global approaches are required because of the complex interdependence of many effects; (2) although the output of the MELTS calculations are imperfect, it is remarkable that, without having been directly constrained to match peridotite phase equilibria, they are so successful.
We must emphasize that some of these inaccuracies and problems with reproducing important features of peridotite partial melting experiments with MELTS calculations limit the applicability of MELTS for understanding some issues in mantle melting. In particular, MELTS calculations cannot be used at this time to explore quantitatively the absolute relationships between temperature, the composition of partial melts, and extent of melting. However, there are in many respects good qualitative or semi-quantitative correspondences between experiment and the MELTS calculations, and because the MELTS calculations are based on an internally consistent thermodynamic formulation of mineral and melt energetics, the trends predicted by these calculations can be used to gain insights into mantle melting processes that are otherwise very difficult to obtain. Such topics include the stoichiometry and energetics of mantle melting, the compositional trends of near-solidus mantle melts, the results of coupled melt flow and reaction in adiabatically upwelling mantle sources, and the effects of variable source composition on the compositions of partial melts (Asimow et al., 1995, 1997; Baker et al., 1995; Hirschmann et al., 1998b).
This work was supported by OCE-9711735 (M.M.H.), OCE-9529790 (M.S.G.), and EAR-9219899 and OCE-9504517 (E.M.S.). This work benefited greatly from discussions with Mike Baker, John Beckett and Sally Newman, and from helpful reviews by Rebecca Lange, Gautam Sen and Ro Kinzler. This paper is Caltech Division of Geological and Planetary Sciences Contribution 6836.
The MELTS algorithm is available free of charge. To download a copy of MELTS, see the MELTS homepage at:
http://www.geology.washington.edu/-ghiorso/MELTsWWW/Melts.html

Table A1: Calculated compositions of phasese in wt % for partila melting of MM3 periodite at 1 GPa and QFM - 1