Geological setting

The Manaslu granite, the most thoroughly studied of all the High Himalayan leucogranites (e.g. Le Fort, 1975, , 1981; Vidal, 1978, , 1982, , 1984; Le Fort et al., 1982, , 1987; Deniel et al., 1987; France-Lanord & Le Fort, 1988; France-Lanord et al., 1988; Copeland et al., 1990; Pêcher, 1991; Guillot et al., 1993, , 1994, , 1995; Guillot & Le Fort, 1995; Harrison et al., 1995b; Chen et al., 1996), is a lenticular body of ~10 km maximum thickness that gently dips to the NNE with a relatively thin sheet, the Chhokang Arm, extending ~60 km to the east of the main body (Fig. 2). The granite is emplaced into, and cuts, a north-verging recumbent anticline developed within Tethyan metasediments (Le Fort, 1981). The base of that fold is truncated by an STDS structure that is itself cut by granitic dikes. There is localized development within the pluton of ductile normal shear with a right lateral component indicating that internal deformation was occurring while the leucogranite was still at high temperature (Guillot et al., 1993, , 1995). Emplacement appears to be largely by dike intrusion with the depth of the roof zone estimated to be ~12 km (Guillot et al., 1993, , 1995). Beneath the STDS are gneisses of the Greater Himalayan Crystallines (GHC) that are themselves juxtaposed atop lower-grade schists of the Lesser Himalayan Formations by the south-directed MCT (Fig. 1). Based on its compositional and isotopic characteristics, the lowermost unit of the GHC (Formation I) is widely believed to represent the unmelted equivalent of the leucogranite source region (e.g. Le Fort, 1981; Barbey et al., 1996).

Figure 2. Geological map of the Manaslu granite and surrounding region. Patterns within the main body of the granite designate the characteristic grain size. Interpreted crystallization ages from Th-Pb monazite dating are shown in the caption boxes. The location of the Rb-Sr isochron result of Deniel et al., (1987) is shown in the black caption box. (See Table 1 for sample identification.) The Nepal-Tibet border is indicated by crosses.

The Manaslu granite is composed of two leucogranite types; a two-mica variety and a less abundant (~20%) tourmaline leucogranite (Guillot & Le Fort, 1995). The generally lower Rb/Sr and initial ⁸⁷Sr/⁸⁶Sr ratio (⁸⁷Sr/⁸⁶Sr_i) of the two-mica leucogranite is broadly similar to that of peraluminous metagraywackes in the Greater Himalayan Crystallines and suggested to Guillot & Le Fort, (1995) that these rocks were the source of melting. Those workers further proposed that the tourmaline leucogranites, which appeared to them to have higher average Rb/Sr and ⁸⁷Sr/⁸⁶Sr_i than the two-mica varieties, were derived via H₂O-undersaturated melting of GHC metapelites.In general, the southwestern side of the pluton is characterized by a relatively fine grain size whereas the central and northeastern portions are generally coarser grained (Fig. 2). Although possibly a reflection in part of different levels of exposure of the laccolith, the textural contrasts between the northeastern and southwestern portions of the Manaslu granite are generally mimicked by several geochemical signatures. The coarser-grained central and northeastern portions of the pluton (Fig. 2) are associated with generally higher Rb/Sr (Fig. 3; see Table 2, below) higher ⁸⁷Sr/⁸⁶Sr_i (>0·752; Deniel et al., 1987), and lower Th/U ratios (<0·7) relative to the southwestern side (Guillot, 1993; see Table 2). An exception to this trend is a restricted region on the southwestern side of the pluton which, in contrast to the encompassing region, is characterized by ⁸⁷Sr/⁸⁶Sr_i ratios of >0·752 (Deniel et al., 1987). We note that these spatially, texturally, and geochemically distinct units contain both two-mica and tourmaline leucogranite varieties.

Figure 3. Contour plot showing variation of Rb/Sr within the Manaslu granite. It should be noted that the southwestern portion of the pluton is characterized by lower Rb/Sr than the central and northeastern portions. Data are taken from Guillot, (1993).

Prior age constraints

Problems inherent in dating High Himalayan leucogranites are in general due to the minimum melt character of these magmas. Heterogeneous ⁸⁷Sr/⁸⁶Sr and ¹⁴³Nd/¹⁴⁴Nd initial ratios (e.g. Vidal et al., 1982; Le Fort et al., 1987) preclude whole-rock isochron dating of the Manaslu granite except in rare cases (e.g. Deniel et al., 1987). U-Pb accessory mineral dating is complicated by the low solubilities of these phases in leucogranite magmas (Harrison & Watson, 1983; Montel, 1993) and the likelihood of their containing an inherited component (Copeland et al., 1988). In general, leucogranite zircons are highly contaminated by inherited Pb* and only rarely appear to yield meaningful crystallization ages (e.g. Schärer et al., 1986). Igneous monazites commonly incorporate significant ²³⁰Th during crystallization; this results in the production of unsupported ²⁰⁶Pb* and obviates the advantages of U-Pb concordia. ⁴⁰Ar/³⁹Ar dating of the Manaslu granite and aureole yield either ~15-19 Ma cooling ages or older dates which reflect contamination by excess ⁴⁰Ar (e.g. Copeland et al., 1990; Guillot et al., 1994; Harrison & Mahon, 1995). Deniel et al., (1987) obtained a single conventional U-Pb monazite age for one Manaslu granite sample. The datum was slightly reversely discordant, because of the presence of unsupported ²⁰⁶Pb*, and thus the ²⁰⁷Pb/²³⁵U age of 25·7 Ma was interpreted as indicating the age of crystallization (Deniel et al., 1987), a view that was later widely accepted (France-Lanord & Le Fort, 1988; Hodges et al., 1988a; Le Fort, 1988; Pêcher, 1991; Chen et al., 1994; Guillot et al., 1994; Villa, 1996).

Harrison et al., (1995a) used ²⁰⁸Pb/²³²Th ion microprobe dating of monazite to constrain the crystallization age for one sample from the southeastern portion of the Manaslu pluton. Because of the short half-lives of the intermediate daughters of ²³²Th, this approach has the advantage of being insensitive to problems of disequilibrium Pb*. Moreover, the spatial resolution of ion microprobe analysis allows measurements of sub-domains of individual monazite crystals so that the question of homogeneity of calculated ages can be explicitly examined. The measurements reported by Harrison et al., (1995a) revealed the presence of a single inherited monazite crystal which yielded ages of ~600 Ma. This result cast doubt on the reliability of the Deniel et al., (1987) datum as representing the emplacement age and led Harrison et al., (1995a) to instead conclude that this rock crystallized at 22·4 ± 0·5 Ma. Despite the seeming clarity of this interpretation, several important questions remain. These include: Is the Manaslu granite homogeneous with respect to crystallization age? Could the single inherited grain be a laboratory contaminant? Is the 22·4 Ma age actually dating metamorphic monazite in the protolith rather than magmatic crystallization? In this paper, we follow up on our analysis of the single sample by presenting dating results of an additional 11 Manaslu granite samples and a neighboring pluton, the Dolpo-Mugu granite. We conclude that these results are consistent with the construction of the Manaslu granite during two phases of early Miocene magmatic activity separated in time by ~4 my, a lag interpreted to reflect the time necessary for the P-T-fluid conditions to alter sufficiently to trigger a second melting event in the same source region.

Th-Pb ion microprobe analyses

The principal advantages of the ²³²Th-²⁰⁸Pb system over the U-Pb method for dating Tertiary monazites are the rapid attainment of secular equilibrium (~30 yr) and high (typically 3-8%) Th concentrations (Montel, 1993) resulting in very high levels of ²⁰⁸Pb*. Uranium concentrations are typically between one and two orders of magnitude lower. The ion microprobe has the demonstrated potential to directly image, and thus avoid, inherited Pb* residing in restitic monazite cores (e.g. Harrison et al., 1995b; Edwards & Harrison, 1997). Given that the melting temperature of Himalayan leucogranites is ~750°C (Montel, 1993; Scaillet et al., 1995), the diffusion of Pb in monazite is sufficiently limited (Smith & Giletti, 1997) to assure a record of crystallization in the cores of >50 µm grains in rocks cooling at >50°C/my. The widespread observation of inheritance (Harrison et al., 1995b; Edwards & Harrison, 1997; this study) confirms this expectation.

The relatively high ionization efficiency of Pb from monazite under O₂^Ö bombardment (~1% useful yield), coupled with high abundances of ²⁰⁸Pb*, permits ²⁰⁸Pb/²³²Th age determinations to be made in an ~5 µm spot on a Tertiary specimen in ~20 min. Details of our analytical methods have been described by Harrison et al., (1995b). A mass resolving power of ~4500 is adequate to separate all molecular interferences (mostly LREE(PO₂)⁺) in the 204-208 mass range. Comparison of ion microprobe Pb isotopic measurements of a synthetic Pb-bearing monazite that was isotopically characterized by thermal ionization mass spectrometry indicates that instrumental mass discrimination is <1%°/a.m.u.

Secondary ion emission from a single crystal target occurs with non-isotropic angular and energy distributions. On our CAMECA ims 1270 ion microprobe, the secondary beam is cut by the entrance and energy slits in planes conjugate to the immersion lens crossover plane of the collection optical system (de Chambost et al., 1991). Secondary-ion distributions in the crossover plane are a function of initial energy and angle of ion emission so that variations in the sputtering conditions at the sample surface (charging, development of topography, etc.) can change the density distributions of Th⁺ and Pb⁺ in these planes and therefore affect the relative sensitivity factor (RSF) for these species. Because sample charging and crater development are believed to be major contributors to these variations, care is taken to control the surface potential and crater depth during analysis. The depth/diameter ratios of the sputtered craters were maintained at <0·1 and monitoring of energy spectra indicates that changes in the average surface potential of the analyzed area under our measurement conditions were <1 eV. In addition, an aperture was inserted into the beam path at an image plane to reject secondary ions emitted from near the edge of the crater, where the extraction field is far from uniform. A further benefit of this optical gating is a substantial reduction of common Pb associated with surface contamination.

The energy distributions of Pb⁺ and Th⁺ secondary ions differ markedly, with Pb⁺ behaving in a fashion similar to a molecular ion (Harrison et al., 1995b). A plot of ²⁶⁴ThO₂⁺/²³²Th⁺ vs ²⁰⁸Pb*⁺/²³²Th⁺ for a standard monazite yields a linear array (the calibration curve) allowing the RSF to be derived by dividing the measured ²⁰⁸Pb*⁺/²³²Th⁺ of the standard at a reference ²⁶⁴ThO₂⁺/²³²Th⁺ value by its known ²⁰⁸Pb*/²³²Th (Fig. 4). The age of an unknown, measured under identical conditions, can then be determined by applying this RSF. For ~20 Ma monazites, the precision of the method is not limited by counting statistics but by the reproducibility of the calibration curve, which is typically ±2%. The accuracy of the method depends critically on usage of a well-characterized standard monazite.

Figure 4. A typical ²⁶⁴ThO₂⁺/²³²Th⁺ vs ²⁰⁸Pb⁺/²³²Th⁺ calibration curve for monazite standard 554 obtained over a period of 1 week. By using the age of 554 (45 ± 1 Ma), this relationship allows a relative sensitivity factor to be calculated, which permits determination of Pb/Th ratios of unknowns measured under the same conditions.

Monazite standard 554

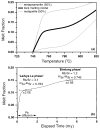
Our primary monazite standard is separated from sample 554, a mildly deformed peraluminous granodiorite from the Santa Catalina Mountains, Arizona [site 82 of Force, (1997)]. The separated monazite contains abundant ~0·2 mm grains that vary from inclusion rich to inclusion free. Prior U-Pb isotope dilution analyses of 554 showed that the sample is too young and U poor (~130 ppm) to yield precise ²⁰⁶Pb/²³⁸U ages (G. Gehrels & R. Parrish, personal communication, 1994). The ²⁰⁶Pb/²³⁸U ages vary between 54 and 45 Ma, whereas the mean ²⁰⁷Pb/²³⁵U age is 46 ± 1 Ma. ²³²Th-²⁰⁸Pb isotope dilution analyses of 11 aliquots of 554 (M. Tatsumoto, personal communication, 1995) produced, with two exceptions, radiogenic yields between 98·9 and 99·8% (assuming common ²⁰⁸Pb/²⁰⁴Pb = 39·5). The two exceptions yielded ²⁰⁸Pb/²⁰⁴Pb ratios consistent with common Pb. We assume that these aliquots contained grains with high densities of fluid inclusions containing high concentrations of common Pb. Omitting the lowest value (>3[sgr] from the mean) yields an age of 45·3 ± 1·4 Ma (2[sgr]). This error is still greater than the <2% dispersion routinely observed on calibration curves for 554 monazite (Fig. 4). This suggests that the grains selected for ion microprobe analysis are uniform in Pb/Th to at least that level. Intercalibration of Th-Pb monazite standards (Harrison et al., 1995b; T. Ireland, personal communication 1995) yields an age for 554 of 45 ± 1 Ma, which is consistent with the isotope dilution results. A further test of the accuracy and reproducibility was undertaken using monazites that were well characterized by U-Pb measurements and could be shown by ion microprobe analyses to have concordant U-Th-Pb systems at the <1% level (Harrison et al., 1995b). Intercalibration of five monazites yields an average dispersion of 1·4% from their known age.

Whole-rock isotopic and trace element analysis

Previous work (e.g. Deniel et al., 1987; Guillot, 1993) has shown that the Manaslu granite is characterized by spatial variability in trace element concentrations and isotopic compositions over multiple length scales. To relate trends observed in the Th-Pb monazite dating to key geochemical indicators, we provide several trace element and isotopic results for the whole-rock samples used in the age determinations. Guided by the earlier investigations, we chose Rb/Sr, ⁸⁷Sr/⁸⁶Sr_i, and Th/U as these parameters. Whole-rock Sm-Nd and Pb isotopic results were also obtained for four samples. Data shown in bold were obtained at UCLA using the methods described by Nelson & Davidson, (1993). All other isotopic results were undertaken at the University of Clermont-Ferrand and are compiled from Deniel et al., (1987) and Guillot, (1993). U and Th were analyzed at CRPG Nancy using the methods of Govindaraju et al., (1976).

Manaslu granite

In an earlier paper we reported Th-Pb ion microprobe dating results on sample U315, located near the base of the pluton where the Chhokang Arm meets the main body of the Manaslu granite (Fig. 2). Two distinct age populations were recognized; the majority of ages defined a normal distribution with a mean age of 22·4 ± 0·5 Ma (±2 SE) that was interpreted to be the age of crystallization. A single inherited grain yielded ages of ~600 Ma (Harrison et al., 1995b).

High-density concentrates were obtained from an additional 11 spatially separated samples (~1 kg each) of the Manaslu granite (Fig. 2) from which monazites were hand picked. Each concentrate yielded ~40-60 monazite grains of ~30-80 µm in size. Twenty grains from each sample were mounted together with the 554 standard in an epoxy disk of 1 inch diameter, ground flat using 1200 SiC grit, polished using 1-; µm diamond paste, cleaned, and sputter coated with ~200 Å of Au. Our initial analyses were undertaken using a 2-3 nA primary beam of O^Ö with a spot size of ~30 µm diameter. All monazite ages reported have been corrected for common Pb based on the average Manaslu whole-rock ²⁰⁸Pb/²⁰⁴Pb ratio of 39·4 ± 0·1 (Table 2; Vidal et al., 1982). Results of all 186 Th-Pb age measurements are available from our web page (http://oro.ess.ucla.edu/ionprobe/manaslu.html), and are summarized in Table 1.

Table 1. Ion microprobe Th-Pb monazite ages

Table 2. Whole-rock isotopic and trace element data for Manaslu granite samples used for Th-Pb geochronology

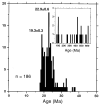
With the exception of XG43, all monazite samples analyzed under the analysis conditions described above yielded an early Miocene age peak with a distribution of individual ages similar in form to that previously seen for U315 (see Table 1). A substantial inherited component was present in most of the samples with prominent ages of ~30-40 Ma and ~100-600 Ma (Table 1). Age assessment of sample XG43 was initially precluded as the dating results yielded a range of ages from 23·8 Ma to ~500 Ma without any distinctive peaks.

Of the 11 results (including U315 but excluding XG43), seven cluster at 22·9 ± 0·3 Ma and four at 19·3 ± 0·3 Ma (Table 1). The younger cluster yields a mean square weighted deviation (MSWD) of 1·4, consistent at the 2[sgr] level with all four samples belonging to a single population. The MSWD of 3·7 for the older cluster is higher than the value of 2·4 expected at the 95% confidence level, suggesting that monazite crystallization occurred over a period of 0·6-1·2 my.

The broad distribution of ages obtained from XG43 (i.e. 23·8 to ~500 Ma) reflects the common occurrence of restitic monazite, which precludes obtaining an estimate of the timing of crystallization, although we interpret the minimum age of 23·8 ± 0·6 Ma to be an upper age limit. With the view that increasing spatial resolution might overcome this problem, we repolished the sample mount and undertook a detailed characterization of a single grain (XG43f) using an analysis spot of ~5 µm diameter. Eighteen Th-Pb analyses of this grain (Fig. 5) revealed an inherited core with ages varying from 102 to 533 Ma and a magmatic rim with an age of 22·7 ± 0·5 Ma (Table 1), consistent with the seven other results from the central and northeastern portions of the pluton. We have previously noted (e.g. Edwards & Harrison, 1997) that the shape of restitic monazite cores inferred from ion microprobe analysis, not otherwise easily imaged by conventional methods, is substantially more irregular that that routinely observed for zircon. All eight samples in the older group (Table 1) yield a mean age of 22·9 ± 0·6 Ma, which we interpret as the crystallization interval. The ⁴⁰Ar/³⁹Ar mica ages for these older rocks average 17·6 ± 0·8 Ma, with none in excess of 18·6 Ma (Copeland et al., 1990). Because no ⁴⁰Ar/³⁹Ar results exceed the interpreted Th-Pb age of the younger intrusive rocks, we infer that rocks in the older group remained at sufficient depth (>10 km; Guillot et al., 1995) to remain open to argon loss or to be reset by the associated thermal pulse. It should be noted from Table 2 that this group is characterized by relatively high Rb/Sr (4-11) and ⁸⁷Sr/⁸⁶Sr_i (>0·752) ratios, suggestive of a derivation from a source containing a mica-rich, metapelitic component. It should be noted also, however, that the seven samples of this age group, although dominantly two-mica leucogranites, also contain tourmaline and two-mica tourmaline varieties.

Figure 5. Photomicrograph of XG43 grain f showing location of spot analyses together with calculated ages in Ma. Although the Au coating is removed from a larger area, the actual size of analyzed region is ~5 µm in diameter.

The four rocks that define the 19·3 ± 0·3 Ma phase are spatially restricted to the southwestern side of the pluton, where Deniel et al., (1987) obtained an Rb-Sr whole-rock isochron relationship on a suite of fine-grained samples (Fig. 2). Recalculation of Rb/Sr data using the algorithm of Mahon, (1996) yields an age of 18·3 ± 0·5 Ma. Mica ⁴⁰Ar/³⁹Ar ages are distinctly younger (15·6 ± 0·6 Ma; Copeland et al., 1990) than those yielded by the older, coarser-grained leucogranite in the central and northeastern portions of the Manaslu granite and are consistent with evidence for greater emplacement depths (~20 km; Guillot et al., 1995). Compared with these rocks (Fig. 2), the ~19 Ma samples have a higher average Th/U (1·1 vs 0·35), and lower Rb/Sr (1-3 vs 4-11) and ⁸⁷Sr/⁸⁶Sr_i (<0·749 vs >0·752) (Table 2; Guillot, 1993). If we assume that these textural and geochemical distinctions are intrinsic to the younger phase and that we can therefore use them as a basis for estimating the fraction of the exposed pluton that was emplaced at 19·6-19·0 Ma, then the ~19 Ma phase represents about one-third of the present exposure of the Manaslu granite. Although this estimate is opposite to that inferred from the bimodal distribution of ⁸⁷Sr/⁸⁶Sr_i ratios (Guillot & Le Fort, 1995) that are dominated by the <0·752 group, geochemical sampling coverage is biased toward the southwestern side of the pluton (Guillot, 1993). Again, we note that the four samples contain both two-mica and two-mica tourmaline leucogranite types. Lastly, we point out that the younger phase yielded no pre-Tertiary monazite ages (Table 1), consistent with much lower levels of restitic monazite compared with the older phase. Because the parameter most sensitive to monazite dissolution is melting temperature, this probably reflects higher peak temperatures for the younger granite. However, other effects, such as a decreased water activity, or a lower abundance of restitic monazite (or a large average grain size) in the source, could also potentially influence monazite dissolution.

The evidence presented for episodic injection of discrete magmas clearly indicates that the Manaslu granite is an intrusive complex and requires us to distinguish between the two magmatic phases thus far recognized. Henceforth, we shall refer to the younger, ~19 Ma, apparently lower ⁸⁷Sr/⁸⁶Sr_i granitoid as the Bimtang phase, and the ~23 Ma, higher ⁸⁷Sr/⁸⁶Sr_i intrusion as the Larkya La phase (see Fig. 3). Because these two plutons contain a complex mixture of two-mica and tourmaline leucogranites, petrologic models emphasizing the need for contrasting physical conditions in the genesis of the different granite types appear not to be supported by our observations (Guillot & Le Fort, 1995).

Dolpo-Mugu granite

The North Himalayan granite belt runs parallel to, and ~80 km to the north of, the High Himalaya (Fig. 1). In contrast to the generally sheet-like High Himalayan leucogranites, the North Himalayan granites belt is composed of ~16 elliptical plutons totaling 4000 km² in area that intrude into Tethyan metasedimentary rocks (Debon et al., 1986; Le Fort, 1986). They differ from the High Himalayan leucogranites in their emplacement style, younger ages (15-9 Ma), and higher melting temperatures as evidenced by noneutectic compositions, lower monazite inheritance, and a monazite saturation temperature of >760°C (Debon et al., 1986; Schärer et al., 1986; Montel, 1993). Their relative youth with respect to the High Himalayan leucogranites has been ascribed to a low rate of fluid infiltration (Le Fort, 1986) and thermal refraction from the Tethyan sedimentary rocks coupled with low heat production (Pinet & Jaupart, 1987).

The Dolpo-Mugu granite (Le Fort & France-Lanord, 1995) is a 1600 km² pluton that straddles the High and North Himalayan belts (Fig. 1). The adjacent Mustang granite appears to have been circular in cross-section before development of the Thakkhola graben, which bisected the pluton and buried its eastern half (Fig. 1). The inferred circular shape of the Mustang granite and its alignment along strike with the northerly belt (Fig. 1) distinguishes it as a North Himalayan granite. Because the Dolpo-Mugu granite straddles the region separating the two belts and is relatively inaccessible, it is difficult to similarly characterize. We undertook Th-Pb monazite dating on a sample of the Dolpo-Mugu granite with the goal of distinguishing with which plutonic series it is most appropriately associated.

Twenty analyses of monazite separated from sample LO68 yield a single population (MSWD = 0·97) with a Th-Pb age of 17·6 ± 0·3 Ma (Table 1). Two splits of the LO68 monazite separate yield isotope dilution Th-Pb ages of 17·13 ± 0·12 and 17·77 ± 0·12 Ma (F. Oberli & M. Meier, personal communication, 1996). Although the isotope dilution ages are separated from each other at the 5[sgr] level, their average value of 17·5 Ma is indistinguishable from the ion microprobe result of 17·6 Ma. Inheritance and/or Pb* loss could explain the difference between the isotope dilution ages, but the normal distribution and MSWD of the ion microprobe age distribution of unity tend to rule out these effects. More likely, this discordance represents a minimum crystallization interval of 0·4-0·6 m.y. It should be noted that the uncertainty on individual ion microprobe spot ages is typically ±0·5 Ma and thus our method is insufficiently precise to distinguish between a single event at 17·6 ± 0·3 Ma and a protracted magmatic history extending over 0·5 my. None the less, this result further demonstrates our ability to accurately date ~17 Ma monazites using our 45 Ma 554 monazite standard.

Manaslu granite

A plot of all 186 Th-Pb spot ages of Manaslu monazites (Fig. 6) clearly reveals two magmatic pulses at ~23 and ~19 Ma, and also shows the spectrum of ages resulting from the incorporation of restitic monazite containing inherited Pb. Interpreting this broad age spectrum in terms of protolith ages is complicated by the potential for hybrid ages to result from diffusive loss and/or overlap of the ion microprobe beam on both rim and core. None the less, we are confident in inferring the existence of at least two restitic monazite components. The clustering of ages between 30 and 40 Ma probably includes monazite formed in the Greater Himalayan Crystallines during Eo-Himalayan metamorphism (Hodges et al., 1996; Le Fort, 1996; Parrish & Hodges, 1996; Edwards & Harrison, 1997). This phase of metamorphism is manifested as higher-pressure prograde assemblages in the GHC that are overprinted by Neogene metamorphism related to slip on the MCT (Pêcher, 1989). The second grouping of ages, between 450 and 600 Ma, probably reflects the effects of Pan African magmatism, which is well documented to have affected the northern margin of the Indian craton, the inferred protolith of the Himalayan gneisses (Le Fort et al., 1982; Schärer & Allègre, 1983; Le Fort et al., 1986; Copeland et al., 1988; Parrish & Hodges, 1996).

Figure 6. Histogram of all 186 Th-Pb monazite ages from the Manaslu intrusive complex. The peaks at 23 Ma and 19 Ma correspond, respectively, to the Larkya La and Bimtang phases. The tailing to much older ages is interpreted as the result of inheritance from ~40 Ma and ~500 Ma protoliths.

Assuming that the crystallization ages given in the caption of Fig. 1 are representative of the plutons from which they were sampled, it appears that about three-quarters of the ~8000 km² of leucogranite exposed along the crest of the High Himalaya (Le Fort et al., 1987), including the Larkya La phase of the Manaslu granite, was emplaced in the relatively brief interval between 24 and 22 Ma.

The Bimtang phase of the Manaslu granite, apparently spatially restricted to the structurally deeper, southwestern side of the intrusive complex, was emplaced at 19·3 ± 0·3 Ma, ~4 my after the Larkya La phase. A leucogranite stock intruded into the Greater Himalayan Crystallines ~30 km to the southwest of the Manaslu granite also yields ~19 Ma U-Pb monazite ages (Coleman & Parrish, 1995) and another small leucogranite body near Nyalam (Fig. 1), ~200 km to the east, yields a similar age (Schärer et al., 1986). Although it is at least arguable that magmatism in the High Himalaya was dominantly bimodal in age with peaks at 23 and 19 Ma, other small bodies yield ages of ~20 and ~17 Ma (Noble & Searle, 1995; Searle et al., 1997), leaving open the possibility that there may have been a continuum of magmatic activity from 24 to ~18 Ma. However, it is clear that models of High Himalayan leucogranite magmatism must account for a minimum duration of 5 my.

The behavior of monazite during anatexis is well understood in terms of its solubility in the melt (Montel, 1993). Once the melt reaches saturation, restitic monazite cores are stabilized in the melt and later provide a site for nucleation of new magmatic monazite. The kinetics of monazite dissolution suggests that crystals of ~50 µm will dissolve relatively rapidly to the point of saturation (Rapp & Watson, 1986) under conditions expected in High Himalayan leucogranite melts (i.e. ~5% H₂O, ~700-775°C; Scaillet et al., 1995). While exposed to the melt, restitic cores passively record the duration of that interval via the diffusive loss of their Pb* to the liquid. In conjunction with accessory mineral thermometry (Harrison & Watson, 1983; Montel, 1993; Ayres et al., 1997), which provides an estimate of peak melting temperature, we can use the ion microprobe to investigate the distribution of Pb* within inherited cores and recover this temporal information. Because of the high Pb* concentrations within inherited cores in these rocks, we can also utilize the U-Th-Pb systems to determine the degree of isotopic re-equilibration.

Although these calculations require some assumptions regarding the mineral dissolution history (see Watson, 1996) and assume that crystal fractionation has not occurred, a first-order estimate of the duration spent at peak temperature, t, can be obtained using the simple relationship t = x²/(D_o e^ÖE/RT), where x represents the maximum length scale of diffusive exchange, estimated from Fig. 5 to be 5 µm, E = 43 kcal/mol, and D_o = 7 * 10^Ö11 cm²/s (Smith & Giletti, 1997). Taking the peak temperature estimated for the Larkya La phase from zircon and monazite saturation thermometry of ~750°C, a monazite-melt interface would produce a surface depletion layer of Pb* with a characteristic length of 5 µm in 0·2 my, with an associated uncertainty of an order of magnitude. With the caveats mentioned above, we conclude that the maximum duration between the melting of the XG43 source rock and emplacement of the magma into the Manaslu pluton was <2 my.

The Th-Pb ion microprobe results presented here appear to resolve the three questions raised in the `Prior age constraints' section with regard to our earlier, solitary result. The Manaslu intrusive complex is heterogeneous with respect to age at the >1 my level, with two phases of intrusion identified at 22·9 ± 0·6 Ma and 19·3 ± 0·3 Ma. The persistence of the ~500 Ma protolith ages in samples with demonstrable ~23 Ma magmatic rims effectively rules out sample contamination as the source of this component. This same grain rim-core age relationship also tends to rule out the possibility that the ~23 Ma ages reflect metamorphic recrystallization. However, monazite that pre-dates magmatism by ~10-15 my is recognized and appears to be related to prograde crystallization of monazite during the Eo-Himalayan phase of collision (Le Fort, 1996).

Dolpo-Mugu granite

Crystallization between 17·9 and 17·1 Ma places this granite at the upper end of the range of ²⁰⁷Pb/²³⁵U monazite ages previously determined for NorthHimalayan granites by Schärer et al., (1986), but below the lower bound for the voluminous High Himalayan leucogranites (Harrison et al., 1997a). Although its structural location, age, and apparent lack of inheritance suggest that the Dolpo-Mugu granite is more akin to that belt than the High Himalayan chain (Harrison et al., 1997a), two issues raised by the present study condition that conclusion. The Dolpo-Mugu granite is one of the largest Tertiary plutons of the Himalayan range (Fig. 1) and, as we have found in the case of the Manaslu massif, one sample is insufficient to characterize a large body. Our results also raise the question of whether Himalayan granitoid magmatism is confined to two separate belts or is in fact a spatiotemporal continuum produced by progressive dehydration melting (Harrison et al., 1999).

Implications for the timing of deformation

Because the Manaslu intrusive complex crosscuts extensional structures in the hanging wall of the detachment, we infer that these features must be older than 19-23 Ma. The phase of syn-magmatic oblique-slip normal shearing within the Larkya La phase must have been active between 23·5 and 22·3 Ma. However, leucogranite dikes observed to crosscut the detachment immediately beneath the southeastern side of the pluton have not been dated.

U-Th-Pb monazite dating of other leucogranite bodies indicates a protracted slip history for the STDS throughout the Himalaya. In the western Himalaya, a small leucogranite in the Zanskar region beneath (and not cut by) the STDS yields an age of 19 ± 1 Ma (Noble & Searle, 1995). Footwall ⁴⁰Ar/³⁹Ar cooling ages between 18 and 15 Ma (T. M. Harrison, unpublished data, 1997) suggest that activity on the basal detachment was probably limited to the interval 20-17 Ma. Near Shisha Pangma, Searle et al., (1997) concluded that the age of normal faulting must largely post-date a leucogranite body dated at 17·3 ± 0·3 Ma. Lastly, in the eastern Himalaya (Fig. 1), the detachment remained active until at least 12·5 ± 0·4 Ma (Edwards & Harrison, 1997).

There are at least three possible explanations for this apparent diachroneity (see Edwards & Harrison, 1997). The first is that the STDS represents a single, northward propagating normal fault system, in which case the variations in age along strike are due to the rollback of the location of the basal detachment. Second, a topographic gradient capable of driving an STDS-type normal fault system may have initiated much later in the eastern Himalaya relative to locations further west. Third, the north-directed thrusts in southeastern Tibet (the Renbu Zedong Thrust System; Quidelleur et al., 1997) may have accommodated STDS displacement in the eastern Himalaya much later than in the western Himalaya.

A mechanism for diachronous leucogranite production from a single source region

Our results present a new challenge to the problem of leucogranite magma genesis. Specifically, how can hundred-km²-sized bodies that differ in age by 4 my be generated from the same crustal source region during continental collision? Below we evaluate whether available models are individually capable, or able when acting in concert, to explain this phenomenon. Our criteria to judge the success of each model in the present context are its ability to predict (1) the emplacement of juxtaposed granite plutons of ~200 km² separated in emplacement age by 4 my, and (2) a decrease in ⁸⁷Sr/⁸⁶Sr_i and Rb/Sr, and concomitant increase in melting temperaturefor the younger phase relative to that of the olderleucogranite.

Le Fort, (1975) proposed that fluids introduced into the GHC from the dehydrating footwall following nappe emplacement fluxed the gneisses to produce the High Himalayan leucogranite melts via minimum melting reactions. Alternatively, Harris et al., (1993) proposed that the leucogranites were produced by higher-temperature, muscovite dehydration melting (e.g. Thompson, 1982) and became mobile only after tectonic decompression (via the STDS) markedly increased the melt fraction. The high Rb/Sr ratios observed in the Himalayan leucogranites seem to preclude the former and heavily favor dehydration melting. Specifically, measured leucogranite Rb/Sr values are typically 2-6 whereas those determined for the GHC source rocks lie in the range 0·7-1·4 (Vidal et al., 1982; Harris et al., 1993). Because the relative proportion of mica (the principal host of Rb in the protolith) to feldspar (the main repository for Sr) consumed in water-saturated melting is small, Rb/Sr ratios are not enriched in minimum melts. Conversely, as breakdown of mica during dehydration melting preferentially releases Rb with respect to Sr, this mechanism has the potential to produce the high Rb/Sr ratios observed for the leucogranites. 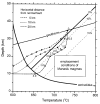Furthermore, recent experimental evidence indicates that water-saturated melting of Himalayan source rocks produces melt of trondhjemitic rather than leucogranitic composition (Patiño Douce & Harris, 1998).

Although such arguments make it seem probable to us that dehydration melting was responsible for Himalayan anatexis, we consider it unlikely that both melting episodes were triggered by tectonic decompression. First, to induce even one melting event requires very high and sustained denudation rates. For example, the melting model of Harris & Massey, (1994) requires >25 km of denudation to produce 8% melting because of decompression, a value which exceeds the maximum structural thickness of the Greater Himalayan Crystallines (e.g. Hodges et al., 1988b). Although other melting models (e.g. Gardien et al., 1995; Fig. 7a) require less exhumation to achieve a similar effect, the issue remains as to whether this effect is capable of generating two magmatic pulses separated temporally by 4 my. We return to this question later, but conclude that tectonic decompression by itself is not a viable mechanism.

Figure 7. (a) Melting relationships of intercalated pelitic and psammitic source rocks used in calculations. The bold curve represents the bulk melting properties derived from melting of a source containing equal quantities of metapelite (long-dashed line) and metapsammite (short-dashed line). (b) Calculated melt fraction in the source region as a function of time since initiation of thrusting. The position of the source region is initially 230 km from the left edge of the numerical grid used by Harrison et al., (1999). The positions on the curves corresponding to the two melting pulses at 11% and 15% total melting are indicated as `Larkya La phase' and Bimtang phase', respectively. The associated error bars reflect the ±2 SE uncertainty on the ages determined in this study. It should be noted that the contrast in age between the two melting peaks of ~4 my is the same as the difference between emplacement of the Larkya La (22·9 ± 0·6 Ma) and Bimtang (19·3 ± 0·3 Ma) phases. The duration of the melting event leading to emplacement of the Larkya La phase, estimated from consideration of the length scale of Pb diffusion in a restitic monazite core, is indicated.

A number of models have linked granite formation to shear heating along the Himalayan thrust system (e.g. Le Fort, 1975; England et al., 1992). Recently, Harrison et al., (1997a, , 1999) suggested that the origin of both the High and North Himalayan granite belts could be linked to shear heating on a continuously active décollement that cuts through Indian supracrustal rocks that were transformed into basement during the initial stages of the Indo-Asian collision. Harrison et al., (1999) approximated the deformation history of the Himalaya and then calculated the distribution of melting that would result from shear heating along the MCT décollement. Assuming a melting relationship that yields pulses of magma at temperatures of 740-750°C and >780°C (Fig. 7a), they found that two temporally distinct granite belts separated by ~80 km (corresponding to the High and North Himalayan chains) could form from shear stresses along the thrust as low as 20-30 MPa. Although High Himalayan leucogranite anatexis as a result of muscovite dehydration melting along the décollement was largely confined to a ~2 my interval in this model, Harrison et al., (1999) demonstrated that an increase in shear stress from 30 MPa to 50 MPa would result in additional, delayed melting from the same source region. Below we explore the extent to which the progressive melting model of Harrison et al., (1999) is capable of explaining the geochemical characteristics of the temporally distinct magmatic phases within the Manaslu intrusive complex.

Harrison et al., (1999) represented the integrated melting properties of the source region by averaging experimentally determined melting relationships for various metasedimentary bulk compositions (Gardien et al., 1995). In the present discussion, we can consider the melt fraction vs temperature relationship as representing the contributions of two sub-equal interlayered components in the GHC source region: muscovite-rich, plagioclase-poor pelitic gneisses and muscovite-poor, plagioclase-rich psammitic rocks (Table 3). The relationships between melt fraction and temperature appropriate for each of these bulk compositions, based upon muscovite and biotite dehydration melting (Le Breton & Thompson, 1988; Gardien et al., 1995), are shown in Fig. 7a. It should be noted that the extent of lower-temperature melting (740-755°C) in each of the lithologies is dictated by muscovite abundance whereas biotite dehydration melting (>785°C) in the metapelite is limited by the complete consumption of plagioclase at higher temperature. Although certain lithologies present in the GHC will be more refractory to melting than indicated by these curves (e.g. Patiño Douce & Harris, 1998), we can rule out candidate source rocks that require melting temperatures >800°C (Montel, 1993).

Table 3. Trace element partitioning and isotopic variation during batch melting

Following the approach of Harrison et al., (1999), but assuming a 50% higher shear stress of 45 MPa, we calculated the melt fraction as a function of time for a given source region position (Fig. 7b). Although the higher shear stress could reflect the dehydration of the thrust surface following the initial phase of melting, variations of other melting parameters [see fig. 7 of Harrison et al., (1999)] could produce the required melting with a lower shear stress. Although we will later conclude that decompression alone cannot trigger the two episodes of leucogranite magmatism, this mechanism could work in concert with frictional heating to reduce the required flow stress to a few hundred bars, which we have previously argued could be maintained along a thrust surface at ~750°C (Harrison et al., 1997a). We also note that because both phases of the Manaslu intrusive complex are emplaced within the hanging wall of the STDS, the source of the ~19 Ma magmatic pulse could be significantly further north within the GHC than the ~23 Ma phase. The higher temperatures further down dip along the MCT would be conducive to the second melting episode appearing earlier than our model predictions and thus be consistent with a lower shear stress.

Coupled to the melting relationship (Fig. 7a), our thermal model predicts that ~11% melt is generated from the heat produced during the initial 1-2 my of slip along the décollement, and an additional 4% is produced after 4-5 my (Fig. 7b). It should be noted that the intervening ~4 my between the initial melting pulse and higher-temperature anatexis is comparable with the interval between emplacement of the Larkya La and Bimtang phases. In addition, the fraction of lower-temperature melt exceeds that produced at higher temperature by a factor of two to three, similar to the inferred proportions of the ~23 Ma and ~19 Ma leucogranite phases. Dropping the flow stress by a factor of two significantly increases the time before appearance of the second melt phase.

Assuming that the leucogranite source region can be characterized by the present exposure of Formation I within the GHC (Guillot & Le Fort, 1995), the melting history (Fig. 7) can be used to predict the trace element and isotope geochemistry of the Manaslu magmas. Rb/Sr and ⁸⁷Sr/⁸⁶Sr_i correlate well with bulk composition in these rocks (Guillot & Le Fort, 1995). On the basis of the data of Vidal et al., (1982) and Deniel et al., (1987), we characterize the metapelites as having Rb/Sr = 2 and ⁸⁷Sr/⁸⁶Sr = 0·765 and the metapsammitic rocks by Rb/Sr = 0·8 and ⁸⁷Sr/⁸⁶Sr = 0·740 (Table 3). Experimentally determined diffusion properties of Sr (e.g. Cherniak & Watson, 1992) of the constituent phases in the >700°C source region lead us to assume that all phases within a given compositional band are equilibrated with respect to ⁸⁷Sr/⁸⁶Sr at the time of anatexis. Using the expression for element partitioning during batch melting together with trace element partition coefficients (Henderson, 1982; Nash & Crecraft, 1985; Harris et al., 1995) yields ⁸⁷Sr/⁸⁶Sr_i = 0·763 and Rb/Sr = 3 for the initial phase of 11% melting (Fig. 7 and Table 3) and ⁸⁷Sr/⁸⁶Sr_i = 0·746 and Rb/Sr = 1·2 for the second, higher-temperature episode that produced an additional 4% melt (Fig. 7 and Table 3). The modal changes during partial melting are dictated by the stoichiometry of reactions specified by equations (2) and (3) of Harris et al., (1995), and the melt contributions from the intercalated pelitic and psammitic sources are integrated to yield the above values (see Table 3). The values of ⁸⁷Sr/⁸⁶Sr predicted by the above calculations agree well with the bimodal distribution observed in the Manaslu complex (Guillot & Le Fort, 1995). Although the calculated values of Rb/Sr are at the lower end of those observed (Guillot & Le Fort, 1995), use of a continuous extraction melting model and different parameters (relative abundance of phases, melt fraction, partition coefficients) can easily generate the range of observed values (see Harris et al., 1993).

The progressive melting model accounts for the ⁸⁷Sr/⁸⁶Sr_i and Rb/Sr systematics of the two intrusive phases, the contrast in emplacement ages, and potentially explains the observed lack of pre-Tertiary monazite inheritance in the Bimtang phase (Table 1) by virtue of its higher-temperature genesis.

Viability of decompression melting for diachronous magmatism

Recognition that most Himalayan anatexis occurred by dehydration melting reactions (e.g. Harris & Inger, 1992) stimulated increasing support for the view that melting was induced by decompression via slip along STDS (e.g. Harris et al., 1993; Harris & Massey, 1994; Guillot & Le Fort, 1995; Searle et al., 1997). Although this enthusiasm is understandable given the positive dP/dT of vapor-absent equilibria, particularly for reactions involving muscovite, the physical viability of this mechanism has not been directly addressed. Data which document diachronous anatexis (Searle et al., 1997; this study) place more specific tectono-thermal requirements upon decompression melting as an explanation for Himalayan anatexis.

To address the feasibility of decompression melting to produce diachronous anatexis, we have undertaken numerical simulations of tectonic denudation owing to extensional faulting. Using the thermal model of Harrison et al., (1995a), P-T-t paths for footwall source regions at differing horizontal distances from a normal fault dipping at 30° were calculated (Fig. 8). Although the present observed dip of the STD is much shallower (Burchfiel et al., 1992), it is unlikely that slip occurred at dip angles much lower than 30° (e.g. Jackson & McKenzie, 1983), and shallower inclinations would require sustained slip rates that are much higher than the total present convergence across the Himalaya (Bilham et al., 1997). To facilitate comparison with the shear-heating model just presented, we used an identical geothermal structure, monitored samples originating from the same initial depth of 35 km (i.e. 10 kbar), and interpret results based upon the same melting model (Fig. 7a). Calculated trajectories of footwall positions at differing distances from the normal fault are shown on a pressure-temperature diagram in Fig. 8 assuming a vertical component of slip of 10 mm/yr, 2·5 mm/yr, and 10 mm/yr for the time intervals 0-1 my (24-23 Ma), 1-3 my (23-21 Ma), and 3-4 my (21-20 Ma), respectively. From these starting conditions, a 10% initial melt can be obtained for source regions located >10 km from the fault given a slip rate of 20 mm/yr (corresponding to 10 mm/yr vertical component). Lower slip rates or positions closer to the normal fault result in source rocks cooling below anatetic conditions (Fig. 8). From inspection of Fig. 8, the magnitude and rate of exhaustion required to obtain two temporally distinct phases of melting seems prohibitive to us. For example, the history shown by the dot-dashed curve in Fig. 8 just succeeds in producing 1% additional melting. Higher degrees of melting would require even more rapid denudation rates than those used here. Moreover, we note that this history does not lead to anatectic or emplacement conditions consistent with those documented for the Manaslu intrusive complex (Copeland et al., 1990; Guillot et al., 1995; Scaillet et al., 1995; see box in Fig. 8).

Figure 8. Pressure-temperature diagram showing calculated trajectories of footwall positions at differing distances from a normal fault dipping at 30° (see Harrison et al., 1995a). Melting conditions shown are: wet melting of metapelites, Le Breton & Thompson, (1988); muscovite-quartz-albite vapor-absent melting, Petö, (1976). Emplacement conditions of the Manaslu magmas are from Scaillet et al., (1995) and Guillot et al., (1995). Vertical component of slip for footwall positions for the various time intervals are: 10 mm/yr, 2·5 mm/yr, and 10 mm/yr for 0-1 my (i.e. 24-23 Ma), 1-3 my (i.e. 23-21 Ma), and 3-4 my (i.e. 21-20 Ma), respectively. Numbers adjacent to the 20 km result are in millions of years and apply to all three curves.

Although we have chosen to illustrate the viability of decompression melting using the same geothermal structure as that used for the shear heating model, use of a significantly lower geotherm (e.g. Harris & Massey, 1994) together with higher slip rates (>20 mm/yr) and total magnitude of denudation (>30 km) could produce better agreement with the known emplacement conditions of the Manaslu intrusive complex (Fig. 8). Despite our reservations regarding the viability of decompression melting, the two models make significantly different, testable predictions that should permit a clear selection between them. For example, a fundamental consequence of the decompression model is that melting occurs at progressively lower pressures and temperatures. In contrast, shear heating along a sub-horizontal décollement results in progressively higher temperature melting. Our inferences from accessory mineral saturation levels and inheritance patterns that the Bimtang phase achieved higher peak temperatures relative to those of the Larkya La phase argues against decompression melting acting alone. Finally, we wish to emphasize that the magnitude of melting from extraordinary decompression (>20-30 km) is matched by only ~40 km of sub-horizontal displacements along the basal décollement assuming modest (<50 MPa) shear stress.